AcWing 839. 模拟堆 —— 对用数组实现映射的一点理解

题目描述

---

函数、映射与数组:

我们都知道一句话那就是：函数是一种特殊的映射。对于数组这种数据结构，其天生具有“映射性”：通过下标索引获得存储在对应索引中的值。如果我们将数组的索引类比函数的输入（定义域中的某个值），存储在索引中的值类比函数的输出（值域中的某个值），是不是数组在一定程度上可以代表一个函数呢。

不妨来看下这个例子：

int f[N];
for (int i = 0; i <= N; i ++) f[i] = i * i;

输出一下 f 数组？

index: 0 1 2 3 ... N 
value: 0 1 4 9 ... N^2

有没有觉得 f 数组在一定程度上代表了 $f(x)=x^2,(0\le x\le N)$呢？

综上，我想表达的是对于算法中的映射关系，我们可以将这种关系想象成函数，再用数组来进行实现。

可以去喝杯咖啡思考一下，或者先来看手工模拟堆这个具体的问题，一会将会直接用上面提出的方法。

---

分析：

补充向下调整（upAdjust），有了解可跳过

在之前堆排序的问题中，我们分析了 downAdjust、createHeap、deleteTop 这三个操作。那如果想要往堆里添加一个元素，应该怎么办呢？可以把想要添加的元素放在数组最后（也就是二叉树的最后一个结点后面，即堆底），然后进行向上调整操作。向上调整总是把欲调整结点与父结点比较，如果值比父结点小，那么就交换其与父结点，这样反复比较，直到达到堆顶或者父结点的权值较小为止，向上调整代码如下，时间复杂度为 $O(logn)$：

void upAdjust(int v)
{
	// v / 2 代表父结点位置
	while (v / 2 && heap[v / 2] > heap[v])
	{
		swap(heap[v], heap[v / 2]);
		v /= 2;
	}
}

用数组代表函数

这样由这四个操作就可以模拟更加复杂的堆了（附加存储位置与插入次序的映射）。在这道题目中由于涉及对第 k 个插入的数操作，因此我们需要新增两个数组：point_heap（记为ph）、heap_to_pinter（记为hp）。
ph[i] = v：堆中第 i 个插入的元素的下标是 v。
hp[v] = i：堆中下标为 v 的位置的元素是第 i 个插入的。

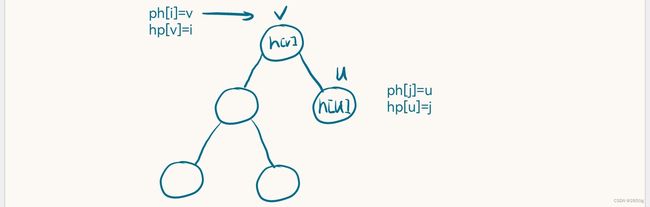
既然每个堆元素的存储位置与插入次序产生了映射关系，当我们想要交换两个堆元素时，其存储位置与插入次序也要进行交换！对于上面的图例，我们不妨按照本文顶部的介绍，用数组来代替函数，在那里的介绍中，我们“刻意而为之”对数组每位赋 i * i 的值，使得 f 数组在一定程度上拟合成了$f(x)=x^2,(0\le x\le N)$。那在本题中这种拟合是怎么发生的呢？从我们的代码中看：

 if (op == "I")
 {
 	cin >> x;
	ssize ++, idx ++; // 堆总数、插入位序增加
            
	// 这是对于《数组实现映射》的不断喂“数据”，使其拟合某个函数
	ph[idx] = ssize, hp[ssize] = idx;
            
	// 新添加数据放在堆底再向上调整
	heap[ssize] = x;
	upAdjust(ssize);
}

每次添加新元素时都是拟合函数的过程。其中：ph 为 $f()$，hp 为 $g()$。i 为 $x_1$，j 为 $x_2$。
上图中四个等式分别为：
$f(x_1)=v$——ph[i]=v \qquad $g(v)=x_1$——hp[v]=i
$f(x_2)=u$——ph[j]=u \qquad $g(u)=x_2$——hp[u]=j
有了这些关系后，我们交换元素时就要把映射考虑进去了。

1. 我们先对存储位置进行交换，即交换 ph 数组：swap(ph[i], ph[j]) 可写成 $swap(f(x_1),f(x_2)$)。但i, j（下标） 即 $x_1,x_2$ （输入）是未知的。
   看看上面的四个等式，我想你一定能明白该如何解决未知量。$swap(f(x_1),f(x_2))=swap[f(g(v)),f(g(u))]$。用程序来表达就是 swap(ph[hp[v]], ph[hp[u]])。
2. 接着对插入次序进行交换，即交换 hp 数组：swap(hp[v], hp[u]) 可写成 $swap(g(v),g(u)$)。这些量都是已知的。
3. 交换完附加信息后，最后我们将元素值进行交换。读者可以思考一下步骤1. 2.能否交换？为什么？

可以看出来带映射关系的堆元素交换操作不再是一个 swap() 能解决的了吧。那我们不如将其写成一个整体，命名为 map_swap()，实现如下：

void map_swap(int v, int u)
{
	swap(ph[hp[v]], ph[hp[u]]); // 存储位置交换
	swap(hp[v], hp[u]) // 插入位序交换
	swap(heap[v], heap[u]); // 堆元素本身的交换
}

另外需要将 downAdjust、upAdjust 中用到的 swap() 都替换成 map_swap()。

下面依次分析一下题目要求的五种操作：
I：添加操作，对于第 idx 个插入的元素，都将其 ph[idx] 设为 ssize（表示堆大小，说明将第 idx 次添加的元素放到堆底处），再把hp[ssize] 设为 idx（说明ssize 位置处的元素是第 idx 次添加的）最后再向上调整。
PM：由小根堆的性质，输出堆顶元素即可。
DM：删除最小元素。首先交换堆顶底元素，减少堆总元素数（代表删除堆底元素操作），对于新来的堆顶元素向下调整即可。
D：删除第 k 个添加的数。首先通过 ph[k] 获取第 k 个添加的数的存储地址，接着与删除最小值步骤相同，只不过是将堆顶元素位置替换成第 k 个添加的元素位置。
C：修改第 k 个添加的数。同上一种操作，也是先取出存储地址，接着修改 heap[存储地址] 即可。

对于删除和修改第 k 个元素，由于会用堆底元素对第 k 个元素进行覆盖，此时有三种情况：

1. 堆底元素等于第 k 个元素，无需操作。
2. 堆底元素比第 k 个元素小，向上调整。
3. 堆底元素比第 k 个元素大，向下调整。

而每次只会出现三者之一，因此可以统一执行 downAdjust(k)、upAdjust(k)。并且这两个函数最多只会执行一个。

---

代码(C++)

#include 
#include 

using namespace std;

const int N = 100010;
// ph[i] = v：堆中第 i 个插入的元素的下标是 v
// hp[v] = i：堆中下标为 v 的位置的元素是第 i 个插入的
int heap[N], ssize, ph[N], hp[N];

void map_swap(int v, int u)
{
    swap(ph[hp[v]], ph[hp[u]]); // 存储位置交换
	swap(hp[v], hp[u]); // 插入位序交换
	swap(heap[v], heap[u]); // 堆元素本身的交换
}

void downAdjust(int v)
{
    // 用 t 来表示子树中的最小值, l 为左孩子位置，r 为右孩子位置
    int t = v, l = v * 2, r = v * 2 + 1;
    // 判断左儿子是否存在以及左孩子值是否小于根结点的值
    if (l <= ssize && heap[l] < heap[t]) t = l;
    // 判断右儿子是否存在以及右孩子值是否小于根结点的值
    if (r <= ssize && heap[r] < heap[t]) t = r;

    // 如果 t 发生了变化（不等于 v）即说明在子树中找到了比根结点更小的值
    // 那么 v 结点就要继续向下调整
    if (v != t)
    {
        // 将其交换，维护小根堆的特性
        map_swap(v, t);
        // 以找到的较小值的位置为根结点继续向下调整
        downAdjust(t);
    }
}

void upAdjust(int v)
{
	// v / 2 代表父结点位置
	while (v / 2 && heap[v] < heap[v / 2])
	{
		map_swap(v, v / 2);
		v /= 2;
	}
}

int main()
{
    int n, idx = 0; // idx 表示插入元素的位序
    cin >> n;
    
    while (n --)
    {
        string op;
        int k, x;
        
        cin >> op;
        if (op == "I")
        {
            cin >> x;
            ssize ++, idx ++; // 堆总数、插入位序增加
            
            // 这是对于《数组实现映射》的不断喂“数据”
            ph[idx] = ssize, hp[ssize] = idx;
            
            // 新添加数据放在堆底再向上调整
            heap[ssize] = x;
            upAdjust(ssize);
        }
        else if (op == "PM") cout << heap[1] << endl;
        else if (op == "DM")
        {
            // 将堆底元素与堆顶元素互换，再向下调整
            map_swap(1, ssize);
            ssize --;
            downAdjust(1);
        }
        else if (op == "D")
        {
            cin >> k;
            // 用 k 获取第 k 个插入的元素在堆中的下标
            k = ph[k];
            map_swap(k, ssize);
            // 删除后，堆总数减一
            ssize --;
            upAdjust(k), downAdjust(k);
        }
        else
        {
            cin >> k >> x;
            k = ph[k];
            // 找到存储位置后，用 x 替换
            heap[k] = x;
            upAdjust(k), downAdjust(k);
        }
    }
}

---