Codeforces Round 875 div.2 problemB. Array merging题解
目录
一、题目
二、题目分析
三、![]()
一、题目
传送门
B. Array merging
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given two arrays a and b both of length n.
You will merge†† these arrays forming another array c of length 2⋅n2⋅. You have to find the maximum length of a subarray consisting of equal values across all arrays c that could be obtained.
†† A merge of two arrays results in an array c,composed by successively taking the first element of either array (as long as that array is nonempty) and removing it. After this step, the element is appended to the back of c. We repeat this operation as long as we can (i.e. at least one array is nonempty).
Input
Each test contains multiple test cases. The first line of input contains a single integer t (1≤t≤104) — the number of test cases. The description of test cases follows.
The first line of each test case contains a single integer n (1≤n≤2⋅105) — the length of the array a and b.
The second line of each test case contains n integers a1,a2,…,an(1≤ai≤2⋅n1) — the elements of array a.
The third line of each test case contains n integers b1,b2,…,bn (1≤bi≤2⋅n1) — the elements of array b.
It is guaranteed that the sum of nacross all test cases does not exceed 2⋅1052⋅105.
Output
For each test case, output the maximum length of a subarray consisting of equal values across all merges.
Example
input:
4
1
2
2
3
1 2 3
4 5 6
2
1 2
2 1
5
1 2 2 2 2
2 1 1 1 1output:
2
1
2
5
Note
In the first test case, we can only make c=[2,2]=[2,2], thus the answer is 22.
In the second test case, since all values are distinct, the answer must be 11.
In the third test case, the arrays c we can make are [1,2,1,2][1,2,1,2], [1,2,2,1][1,2,2,1], [2,1,1,2][2,1,1,2], [2,1,2,1][2,1,2,1]. We can see that the answer is 22 when we choose c=[1,2,2,1]=[1,2,2,1].
二、题目分析
1.题意为每次从a或b中拿走第一个元素放入新数组c中,问在数组c中最多能有多少连续重复的数。
2.思路:因为要每次从a或b中取出第一个元素,那么想要让连续的最多,最好的办法就是a,b中连续最多。因为最终的数组源于两个数组,所以要进行更新。
三、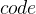
int n,v1,p=-1,ans=0,sam=1;
cin>>n;
int t[2*n+5]={};
for(int i=0;i>v1;
if(v1==p)sam++;
else sam=1;
t[v1]=max(t[v1],sam);
p=v1;
}
p=-1;
sam=1;
for(int i=0;i>v1;
if(v1==p)sam++;
else sam=1;
ans=max(ans,sam+t[v1]);
p=v1;
}
for(int i=0;i<=2*n;i++)ans=max(ans,t[i]);
cout<