数据结构-图详解(最短路径问题-Dijkstra,Bellman-Ford,Floyd-Warshall算法 -C++)
与图有关的基本概念
文章目录
- 1.最短路径
- 2.单源最短路径
-
- Ⅰ.Dijkstra算法
-
- 算法思路
- 执行过程
- C++代码实现
- Ⅱ.Bellman-Ford算法
-
- 算法思路
- 负权回路问题
- C++代码实现
- 3.多源最短路径
-
- Ⅰ.Floyd-Warshall算法
-
- 算法思路
- C++代码实现
- 4. 代码位置
1.最短路径
最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
图的生成树针对的是无向图,图的最短路径一般是针对的是有向图。
2.单源最短路径
单源最短路径问题:给定一个有向图G = ( V , E ) ,求源结点s ∈ V到图中每个结点v ∈ V 的最短路径
给一个点A,A点到图的其他点的最短路径。
Ⅰ.Dijkstra算法
Dijkstra算法适用于解决带权重的有向图上的单源最短路径问题,同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点 和一个终点,所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。
注意:
Dijkstra算法效率很高,但是只适合有向图权值不是负数的情况
如果出现权值为负数的单源最短路径问题,只能使用Bellman-Ford算法。
算法思路
- 把有向图所有顶点分成两组。S组是已经确定最短路径的顶点集合,初始化为源节点(源节点到自己的代价是0,最短路径已经确定)。Q组是未确定最短路径的顶点的集合,初始化为所有节点包含源节点。
- 每次从Q组找一个起点到源节点路径最小的节点P,将P点从Q集合中移除放入S集合中,并且对节点P的所有相邻节点adjoinPonits进行松弛操作
(松弛操作:即对每一个相邻结点adjoinPoint ,判断源节点到结点P 的代价与P点 到adjoinPoint 的代价之和是否比原节点 到adjoinPoint 的代价更小,若代价小则要将源节点 到adjoinPoint 的代价更新为源节点 到P 与P 到adjoinPoint 的代价之和,否则维持原样。) - 如此一直循环直至集合Q 为空,即所有节点都已经查找过一遍并确定了最短路径,至于一些起点到达不了的结点在算法循环后其代价仍为初始设定 的值,不发生变化
Dijkstra算法每次都是选择adjoinPoints相邻节点-S中最小的路径节点来进行更新,并加入S组中,所 以该算法使用的是贪心策略。
需要特别注意的是:上图中的节点代表的是源节点到这个点的最小距离。
执行过程
-
开始集合S为源节点(每个结点中的数值为该结点的最短路径的估计值),开始时源顶点到自己的最短路径为0,所以节点上的值为0。其他最段路径先初始化为默认值。
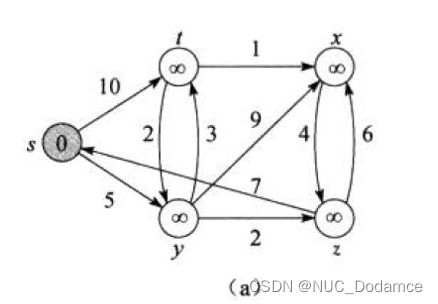
-
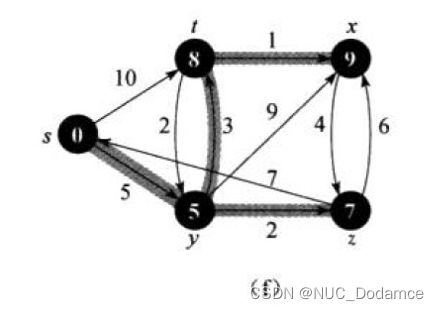
第一次处理的时源顶点,先从Q组找一个起点到源节点路径最小的节点就是这个源节点(P点)。源节点到P点的距离为0,P对所有的相邻节点(adjoinPoint)的距离为5和10(即上图的t、y点)。
源节点到结点P 的代价(代价为0)与P点 到adjoinPoint 的代价和(5+0和10+0)与源节点到adjoinPoint代价(无穷(默认值))相比要小,根据上面的过程分析,需要将源节点 到adjoinPoint 的代价更新为源节点 到P 与P 到adjoinPoint 的代价之和。
将P点从Q集合中移除放入S集合中(此时因为P就是源节点,在S集合中本来就存在,不需要添加了,要不然S集合就重复添加源节点了),此时S集合有一个顶点(源顶点)用黑色表示,Q集合有的点:t、y、x、z点

-
第二次循环,先从Q组找一个起点到源节点路径最小的节点P,如上图可知选出来的点是y顶点(P点)。将P点从Q集合中移除放入S集合中,并且对节点P的所有相邻节点adjoinPonits进行松弛操作。
源节点到节点P的代价(代价为5)与P点到P所有相邻节点(adjoinPoint )代价和(代价为3+5,9+5,2+5)与源节点到adjoinPoint代价相比。根据上面的算法思路过程分析:若代价小则要将源节点 到adjoinPoint 的代价更新为源节点 到P 与P 到adjoinPoint 的代价之和,否则维持原样。
①源节点到节点P的代价与P点到t点(其中一个相邻节点)代价和为3+5=8 相比与源节点到t点代价(10)小,将源节点到t的距离更新为8
②源节点到节点P的代价与P点到x点(其中一个相邻节点)代价和为14与源节点到x的代价(无穷大)相比要小,将源节点到x的距离更新为14
③源节点到节点P的代价与P点到z点的代价和为7,小于源节点到z点的代价(无穷),将源节点到z的距离更新为7。

将P点从Q集合中移除放入S集合中,此时S集合有一个顶点(源顶点)用黑色表示,Q集合有的点:t、x、z点。 -
第三次,先从Q组找一个起点到源节点路径最小的节点P,P点就是图中的z点。将P点从Q集合中移除放入S集合中,并且对节点P的所有相邻节点adjoinPonits进行松弛操作。
P点相邻的节点有x,s点,源节点到x点距离根据上图可知为14,源节点到P与P到x代价和为7+6=13,两者相比把小的更新到源节点到x代价即可。
容易得知,s到s最小路径为0,不需要更改路径。
Q集合有的点:t、x点。

贪心策略:
每次选出Q集合中到源顶点路径最小的点P,通过这两个顶点构成的边来更新源节点到P直接相邻的点的路径长度。这样选择一定是当前过程最优解。
C++代码实现
这里使用邻接矩阵保存边关系
顶点保存在dist数组中,数组下标代表顶点编号,数组下标值代表源顶点到这个顶点的最短路径长度。初始化默认值(无穷)
为了保存最短路径之间的节点,这里使用数组pPath的形式保存每一个顶点的父节点。(存储的是路径中所有顶点最短路径的前一个顶点下标)数组初始化为-1。
类似并查集找根节点的过程.
namespace matrix {
//邻接矩阵保存边关系
template<class v, class w, w max_w = INT_MAX, bool Direction = false>
class Graph {
typedef Graph<v, w, max_w, Direction>Self;
private:
std::vector<v>_vertexs;//顶点集合
std::map<v, int>_indexMap;//顶点与下标的映射
std::vector<std::vector<w>>_matrix;//邻接矩阵
//获取顶点下标
size_t GetPointIndex(const v& point) {
auto ptr = _indexMap.find(point);
if (ptr != _indexMap.end()) {
return ptr->second;
}
else {
throw std::invalid_argument("顶点不存在");
return -1;
}
}
public:
//图的创建
Graph() = default;
Graph(std::vector<v>& points) {
_vertexs.resize(points.size());
for (size_t i = 0; i < points.size(); i++) {
_vertexs[i] = points[i];
_indexMap[points[i]] = i;
}
_matrix.resize(points.size());
//邻接矩阵
for (int i = 0; i < _matrix.size(); i++) {
_matrix[i].resize(points.size(), max_w);
}
}
//添加边关系,输入两个点,以及这两个点连线边的权值。
private:
void _AddEdge(size_t posSrc, size_t posDst, const w& weight) {
//区分有向图与无向图
_matrix[posSrc][posDst] = weight;
if (Direction == false) {
//无向图,添加两条边关系
_matrix[posDst][posSrc] = weight;
}
}
public:
void AddEdge(const v& src, const v& dst, const w& weight) {
size_t posSrc = GetPointIndex(src);
size_t posDst = GetPointIndex(dst);
_AddEdge(posSrc, posDst, weight);
}
public:
//单源最短路径
//src:源顶点 dist保存src到各个顶点的最短距离 pPath:保存最短路径的节点
void Dijkstra(const v& src, std::vector<w>& dist, std::vector<int>& pPath) {
size_t srcPos = GetPointIndex(src);
size_t size = _vertexs.size();
dist.resize(size, max_w);
pPath.resize(size, -1);
dist[srcPos] = 0;//源顶点到自己本身最短距离为0
pPath[srcPos] = srcPos;//源顶点的最短路径的父节点是自己本身
std::vector<bool>S(size, false);//已经确定最短路径的顶点的集合
//循环判断所有的顶点
for (size_t time = 0; time < size; time++) {
//选不在S集合 最短路径的顶点,更新其他路径
//选p点,p点不在S集合中
int p = 0;
w min = max_w;//最小权值
for (size_t i = 0; i < size; i++) {
if (S[i] == false && dist[i] < min) {
p = i;
min = dist[i];
}
}
//把p点放入S集合中
S[p] = true;
//松弛更新 src->p + p->p邻接节点 与 src ->p邻接节点权值相比较小,要更新
for (size_t adP = 0; adP < size; adP++) {
//找p点所有的邻接顶点
if (S[adP] == false && _matrix[p][adP] != max_w) {
if ((dist[p] + _matrix[p][adP]) < dist[adP]) {
dist[adP] = dist[p] + _matrix[p][adP];
//更新这个顶点最短路径的父节点
pPath[adP] = p;
}
}
}
}
}
//打印最短路径
void PrintShortPath(const v& src, std::vector<w>& dist, std::vector<int>& pPath) {
size_t srcPos = GetPointIndex(src);
size_t size = _vertexs.size();
//计算src点到其他点的最短路径长度,src到src=0不用计算
for (size_t i = 0; i < size; i++) {
if (i != srcPos) {
//src到顶点i的最短路径节点(双亲表示法)
std::vector<int>path;
size_t pos = i;
std::cout <<"最短路径为:";
while (pos != srcPos) {
path.push_back(pos);
pos = pPath[pos];
}
path.push_back(srcPos);
std::reverse(path.begin(), path.end());
for (auto index : path) {
std::cout << _vertexs[index] << "->";
}
std::cout << "长度:" << dist[i];
std::cout << std::endl;
}
}
}
};
}
测试:
#include"Graph.h"
using namespace std;
void TestGraphDijkstra()
{
vector<char> str = { 's','y','z','t','x' };
matrix::Graph<char, int, INT_MAX, true> g(str);
g.AddEdge('s', 't', 10);
g.AddEdge('s', 'y', 5);
g.AddEdge('y', 't', 3);
g.AddEdge('y', 'x', 9);
g.AddEdge('y', 'z', 2);
g.AddEdge('z', 's', 7);
g.AddEdge('z', 'x', 6);
g.AddEdge('t', 'y', 2);
g.AddEdge('t', 'x', 1);
g.AddEdge('x', 'z', 4);
vector<int> dist; vector<int> parentPath;
g.Dijkstra('s', dist, parentPath);
g.PrintShortPath('s',dist, parentPath);
}
int main() {
TestGraphDijkstra();
}
算法的空间复杂度:开辟了二个大小等于顶点个数的数组,O(N)
时间复杂度:N个顶点,每个顶点都需要遍历一遍这个顶点的邻接顶点。时间复杂度O(N^2);
Ⅱ.Bellman-Ford算法
因为Dijkstra不适合权值为负数的情况,而Bellman-Ford算法能够解决权值为负数的情况,但是效率没有Dijkstra算法快。
算法思路
Bellman-Ford与Dijkstra不同的是边的更新策略。
- Dijkstra:是找权值最小的起始边,之后再找起始边相连的其他边,本质是贪心算法
- Bellman-Ford:是找最终边,本质是暴力遍历。
根据上图可知,起点s到图中的其他顶点。要么直接相连,要么通过其他的顶点间接相连。
简述为:s->j 或者 s->i+i->j
- 以i->j这条边为起始边(找最终边)如果找到了(s->i+i->j)< s->j时进行松弛变化。(变化规则与Dijkstra算法相同)将s->j的权值修改为s->i+i->j
- s->j这里代表图中的所有边。所有的边都需要进行与其他边松弛判断。
注意:
这里可能出现权值与路径不匹配。
eg:开始计算s->t的最小值为6,此时计算s->t->z的值为2。(图c)
之后s->t的最小值变成了s->y->x->t最小值变成2(图d),此时必须修改上一步的结果图(e),如果没有修改就会出现路径和权值不匹配的情况。
只要更新出最短路径,就可能影响其他路径。解决这个问题的方式就是再整体更新一次。一旦更新有可能会影响其他路径,但是最多更新顶点次数,所以直接暴力更新顶点次数次即可。
如果这次遍历没有更新边,则后面的重复暴力就可以停止了。
负权回路问题
Bellman-Ford算法可以解决负权图的单源最短路径问题。但是解决不了负权回路问题。
负权回路:s->s最短路径权值计算为负数。
eg:
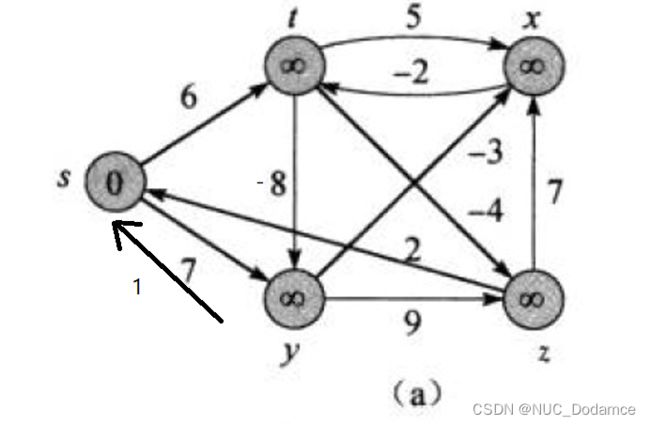
如上图s->s最短路径为s->t->y->s 为-1,那么只要重读次数足够多,s->s的最短路径可以一直变小。
重复两次为-2,重读三次为-3,有根据上文可知更新最短路径,就可能影响其他路径。所以此时最短路径会一直更新,Bellman-Ford算法没办法解决。
C++代码实现
namespace matrix {
//邻接矩阵保存边关系
template<class v, class w, w max_w = INT_MAX, bool Direction = false>
class Graph {
typedef Graph<v, w, max_w, Direction>Self;
private:
std::vector<v>_vertexs;//顶点集合
std::map<v, int>_indexMap;//顶点与下标的映射
std::vector<std::vector<w>>_matrix;//邻接矩阵
//获取顶点下标
size_t GetPointIndex(const v& point) {
auto ptr = _indexMap.find(point);
if (ptr != _indexMap.end()) {
return ptr->second;
}
else {
throw std::invalid_argument("顶点不存在");
return -1;
}
}
public:
//图的创建
Graph() = default;
Graph(std::vector<v>& points) {
_vertexs.resize(points.size());
for (size_t i = 0; i < points.size(); i++) {
_vertexs[i] = points[i];
_indexMap[points[i]] = i;
}
_matrix.resize(points.size());
//邻接矩阵
for (int i = 0; i < _matrix.size(); i++) {
_matrix[i].resize(points.size(), max_w);
}
}
//添加边关系,输入两个点,以及这两个点连线边的权值。
private:
void _AddEdge(size_t posSrc, size_t posDst, const w& weight) {
//区分有向图与无向图
_matrix[posSrc][posDst] = weight;
if (Direction == false) {
//无向图,添加两条边关系
_matrix[posDst][posSrc] = weight;
}
}
public:
void AddEdge(const v& src, const v& dst, const w& weight) {
size_t posSrc = GetPointIndex(src);
size_t posDst = GetPointIndex(dst);
_AddEdge(posSrc, posDst, weight);
}
public:
//单源最短路径
//src:源顶点 dist保存src到各个顶点的最短距离 pPath:保存最短路径的节点
//如果出现负权回路。函数返回false值
bool BellmanFord(const v& src, vector<w>& dist, vector<int>& pPath) {
size_t size = _vertexs.size();
size_t srcPos = GetPointIndex(src);
// vector dist,记录srcPos-其他顶点最短路径权值数组
dist.resize(size, max_w);
// vector pPath 记录srcPos-其他顶点最短路径父顶点数组
pPath.resize(size, -1);
// 先更新srci->srci为缺省值0
dist[srcPos] = w();
// 总体最多更新size轮
for (size_t time = 0; time < size; time++) {
// i->j 更新松弛
bool update = false;
for (size_t i = 0; i < size; i++) {
for (size_t j = 0; j < size; j++) {
// srcPos -> i + i ->j松弛判断
if (_matrix[i][j] != max_w && (dist[i] + _matrix[i][j]) < dist[j]) {
dist[j]= dist[j] = dist[i] + _matrix[i][j];
update = true;
pPath[j] = i;
}
}
}
if (update == false) {
break;//这次没有更新出最短路径,可以退出循环了
}
}
//判断负权回路,如果退出循环还可以更新,就是负权回路返回false
// 还能更新就是带负权回路
for (size_t i = 0; i < size; ++i)
{
for (size_t j = 0; j < size; ++j)
{
if (_matrix[i][j] != max_w && dist[i] + _matrix[i][j] < dist[j])
{
return false;
}
}
}
return true;
}
//打印最短路径
void PrintShortPath(const v& src, std::vector<w>& dist, std::vector<int>& pPath) {
size_t srcPos = GetPointIndex(src);
size_t size = _vertexs.size();
//计算src点到其他点的最短路径长度,src到src=0不用计算
for (size_t i = 0; i < size; i++) {
if (i != srcPos) {
//src到顶点i的最短路径节点(双亲表示法)
std::vector<int>path;
size_t pos = i;
std::cout <<"最短路径为:";
while (pos != srcPos) {
path.push_back(pos);
pos = pPath[pos];
}
path.push_back(srcPos);
std::reverse(path.begin(), path.end());
for (auto index : path) {
std::cout << _vertexs[index] << "->";
}
std::cout << "长度:" << dist[i];
std::cout << std::endl;
}
}
}
};
}
测试:
void TestGraphBellmanFord()
{
vector<char> str = { 's','y','z','t','x' };
matrix::Graph<char, int, INT_MAX, true> g(str);
g.AddEdge('s', 't', 6);
g.AddEdge('s', 'y', 7);
g.AddEdge('y', 'z', 9);
g.AddEdge('y', 'x', -3);
g.AddEdge('z', 's', 2);
g.AddEdge('z', 'x', 7);
g.AddEdge('t', 'x', 5);
g.AddEdge('t', 'y', 8);
g.AddEdge('t', 'z', -4);
g.AddEdge('x', 't', -2);
vector<int> dist;
vector<int> parentPath;
g.BellmanFord('s', dist, parentPath);
g.PrintShortPath('s', dist, parentPath);
//vector str = { 's','y','z','t','x' };
//matrix::Graph g(str);
//g.AddEdge('s', 't', 6);
//g.AddEdge('s', 'y', 7);
//g.AddEdge('y', 'z', 9);
//g.AddEdge('y', 'x', -3);
//g.AddEdge('y', 's', 1); // 新增
//g.AddEdge('z', 's', 2);
//g.AddEdge('z', 'x', 7);
//g.AddEdge('t', 'x', 5);
//g.AddEdge('t', 'y', -8); //更改
g.AddEdge('t', 'y', 8);
//g.AddEdge('t', 'z', -4);
//g.AddEdge('x', 't', -2);
//vector dist;
//vector parentPath;
//if (g.BellmanFord('s', dist, parentPath))
// g.PrintShortPath('s', dist, parentPath);
//else
// cout << "带负权回路" << endl;
}
int main() {
TestGraphBellmanFord();
}
优点
- 可以解决有负权边的单源最短路径问题,而且可以用来判断是否有负权回路
缺点
- 时间复杂度O(N^3),比较慢。
拓展:Bellman-Ford算法可以通过优先级队列进行优化,优化后称为SPFA 算法
3.多源最短路径
多源最短路径:源顶点是图中的所有顶点,求图中任意两点的最短路径。
Ⅰ.Floyd-Warshall算法
注意:
- Floyd-Warshall可以解决负数权值问题。
- 如果以所有点为源点,使用Dijkstra算法也可以算出图中任意两点的最短路径。但是Dijkstra算法不能带负数权值,Bellman-Ford算法效率太低。
因为Floyd-Warshall算法要以图中任意顶点为源顶点。
根据上面分析可知,dist(记录源顶点到其他顶点的最短路径)数组应该是二维数组。
pPath(通过双亲表示法记录最短路径的节点)也应该是二维数组。
算法思路
Floyd算法考虑的是一条最短路径的中间节点,即简单路径p={v1,v2,…,vn}上除v1和vn的任意节点。
设k是p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。p1 是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1, 2,…,k-1}取得的一条最短路径。
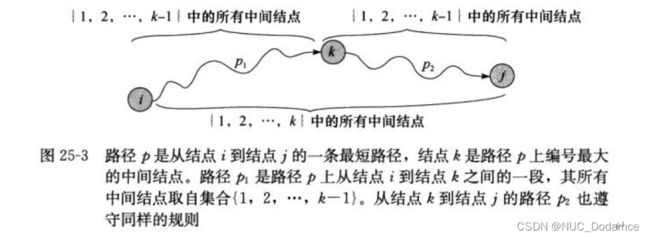
简单来讲,设图中有n个顶点
图中的任意两点之间之间可能没有顶点,也可能有顶点。任意两点之间最多有k个(n-2)顶点。

简单来讲:如果k是i->j之间的点且(i->k+k->j)< i->j说明经过中点k会使路径更短,更新i->j的路径长度。并且修改Path数组,记录更新后的父顶点。

左边的是权值矩阵,右边的是父节点矩阵。与上面类似,只不过Floyd-Warshall算法要把图中的每个顶点都做一遍源节点,所以最后是二维数组
C++代码实现
namespace matrix {
//邻接矩阵保存边关系
template<class v, class w, w max_w = INT_MAX, bool Direction = false>
class Graph {
typedef Graph<v, w, max_w, Direction>Self;
private:
std::vector<v>_vertexs;//顶点集合
std::map<v, int>_indexMap;//顶点与下标的映射
std::vector<std::vector<w>>_matrix;//邻接矩阵
//获取顶点下标
size_t GetPointIndex(const v& point) {
auto ptr = _indexMap.find(point);
if (ptr != _indexMap.end()) {
return ptr->second;
}
else {
throw std::invalid_argument("顶点不存在");
return -1;
}
}
public:
//图的创建
Graph() = default;
Graph(std::vector<v>& points) {
_vertexs.resize(points.size());
for (size_t i = 0; i < points.size(); i++) {
_vertexs[i] = points[i];
_indexMap[points[i]] = i;
}
_matrix.resize(points.size());
//邻接矩阵
for (int i = 0; i < _matrix.size(); i++) {
_matrix[i].resize(points.size(), max_w);
}
}
//添加边关系,输入两个点,以及这两个点连线边的权值。
private:
void _AddEdge(size_t posSrc, size_t posDst, const w& weight) {
//区分有向图与无向图
_matrix[posSrc][posDst] = weight;
if (Direction == false) {
//无向图,添加两条边关系
_matrix[posDst][posSrc] = weight;
}
}
public:
void AddEdge(const v& src, const v& dst, const w& weight) {
size_t posSrc = GetPointIndex(src);
size_t posDst = GetPointIndex(dst);
_AddEdge(posSrc, posDst, weight);
}
public:
void FloydWarShall(std::vector<std::vector<W>>& vDist, std::vector<std::vector<int>>& vPath) {
size_t size = _vertexs.size();
//初始化顶点矩阵与路径矩阵
vDist.resize(size);
vPath.resize(size);
for (size_t i = 0; i < size; i++) {
vDist[i].resize(size, max_w);
vPath[i].resize(size, -1);
}
//直接相连的边更新初始化
for (size_t i = 0; i < size; i++) {
for (size_t j = 0; j < size; j++) {
if (_matrix[i][j] != max_w) {
vDist[i][j] = _matrix[i][j];
vPath[i][j] = i;//i->j起点是i点
}
if (i == j) {
//i->i时路径长度为0
vDist[i][j] = w();
}
}
}
//最短路径的更新i->{其他顶点}->j
//k作为中间点,尝试更新i->j的路径
for (size_t k = 0; k < size; k++) {
for (size_t i = 0; i < size; i++) {
for (size_t j = 0; j < size; j++) {
//经过了k点
if (vDist[i][k] != max_w && vDist[k][j] != max_w) {
if ((vDist[i][k] + vDist[k][j]) < vDist[i][j]) {
//经过k更小,则更新长度
vDist[i][j] = vDist[i][k] + vDist[k][j];
//找上一个与j邻接的节点
//k->j入过k与j直接相连,则vPath[i][j]=k
//但是k->j不一定直接相连 k->...->x->j则vPath[i][j]=x,就是vPath[k][j]
vPath[i][j] = vPath[k][j];
}
}
}
}
}
}
//打印最短路径
void PrintShortPath(const v& src, std::vector<w>& dist, std::vector<int>& pPath) {
size_t srcPos = GetPointIndex(src);
size_t size = _vertexs.size();
//计算src点到其他点的最短路径长度,src到src=0不用计算
for (size_t i = 0; i < size; i++) {
if (i != srcPos) {
//src到顶点i的最短路径节点(双亲表示法)
std::vector<int>path;
size_t pos = i;
std::cout <<"最短路径为:";
while (pos != srcPos) {
path.push_back(pos);
pos = pPath[pos];
}
path.push_back(srcPos);
std::reverse(path.begin(), path.end());
for (auto index : path) {
std::cout << _vertexs[index] << "->";
}
std::cout << "长度:" << dist[i];
std::cout << std::endl;
}
}
}
};
}
测试:
void TestFloydWarShall()
{
vector<char> str = { '1','2','3','4','5' };
matrix::Graph<char, int, INT_MAX, true> g(str);
g.AddEdge('1', '2', 3);
g.AddEdge('1', '3', 8);
g.AddEdge('1', '5', -4);
g.AddEdge('2', '4', 1);
g.AddEdge('2', '5', 7);
g.AddEdge('3', '2', 4);
g.AddEdge('4', '1', 2);
g.AddEdge('4', '3', -5);
g.AddEdge('5', '4', 6);
vector<vector<int>> vDist; vector<vector<int>> vPath;
g.FloydWarShall(vDist, vPath);
// 打印任意两点之间的最短路径
for (size_t i = 0; i < str.size(); ++i)
{
g.PrintShortPath(str[i], vDist[i], vPath[i]);
cout << endl;
}
}
int main() {
TestFloydWarShall();
}
分别是以图的不同顶点为源顶点的最短路径
4. 代码位置
Github
码云