（数字图像处理MATLAB+Python）第十一章图像描述与分析-第三、四节：几何表述和形状描述

一：几何描述

（1）像素间几何关系

A：邻接与连通

前景与背景：

• 前景： 指的是图像中的目标或感兴趣的物体，通常具有较高的像素值（亮度或颜色），并且在视觉上与其他部分区分开来。在像素级别，前景像素通常集中在一起，形成连续的区域，表示目标的外轮廓或内部信息
• 背景： 是指前景之外的图像区域，它通常包含着前景，并提供了前景的环境和上下文信息。背景像素通常具有较低的像素值（亮度或颜色），并且在视觉上与前景区域有所区别

在几何关系方面，前景和背景之间存在多种关系，如：

• 前景-背景分割：这是图像处理和计算机视觉中的一个重要任务，即将图像中的前景目标从背景中分割出来。通过分析像素的几何关系、像素值和纹理等特征，可以进行前景-背景分割，以识别和提取出感兴趣的目标区域
• 前景-背景交互：在图像中，前景和背景可能相互作用或相互影响。例如，在人物摄影中，主体通常是前景，背景则提供了合适的背景环境。通过调整前景和背景之间的关系，可以实现更好的视觉效果
• 前景-背景约束：在计算机视觉领域，前景和背景之间的几何关系可以用于约束分析和处理的结果。例如，在对象识别中，通过考虑前景和背景之间的边界、比例关系等几何特征，可以提高目标检测和分类的准确性

路径与连通：

• 路径： 指的是从一个像素到另一个像素的连续线条或曲线。在图像处理和计算机视觉中，路径常用于描述物体的边界、轮廓或者像素之间的连接关系。路径可以按照不同的形式进行表示，比如二值图像中的像素序列、连续边缘点、多边形等
  • 轮廓路径：在目标分割和识别中，轮廓路径表示了目标的外形边界，通过连接目标边界上的像素点而形成。
  • 骨架路径：骨架路径也称为中轴线，表示了目标的主要结构或形态特征，是由目标内部的像素点连接而成
• 连通： 指的是像素之间的直接邻接关系，即相邻像素之间通过共享边或角来连接。在像素级别，连通性可以根据四邻域或八邻域进行定义，四邻域表示上下左右四个相邻像素，八邻域表示上下左右以及对角线方向的八个相邻像素
  • 4连通：在四邻域中，如果两个像素之间共享一条边，则它们被认为是4连通的。
  • 8连通：在八邻域中，如果两个像素之间共享一条边或者一个角，则它们被认为是8连通的
    

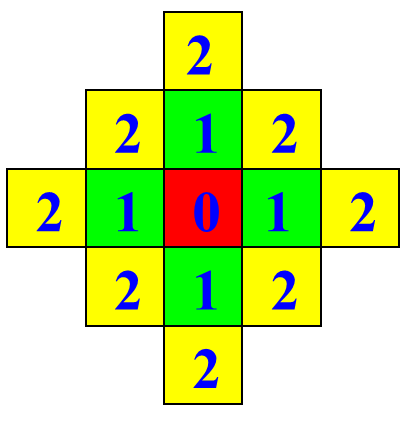
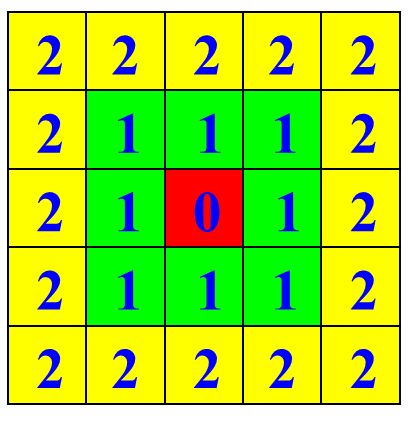
B：距离

距离：对于像素$p$、$q$和$z$，如果满足以下三个条件，则称$d$是距离函数或度量

• $d(p,q)\ge 0$
• $d(p,q)=d(q,p)$
• $d(p,z)\le d(p,q)+d(q,z)$

其中，欧式距离是指

$$D_e(p,q)=\sqrt{(x-s{)}^2+(y-t{)}^2}$$

---

城市距离：$D_4(p,q)=|x-s|+|y-t|$

棋盘距离：$D_8(p,q)=max(|x-s|,|y-t|)$

（2）像素间几何特征

A：位置

位置：物体在图像中的位置，用物体面积的中心点来表示。二值图像质量分布是均匀的,质心和形心重合。若图像中的物体对应的像素位置坐标为$(x_i,y_i)(i=0,1,\dots ,n－1；j=0,1,\dots ,m－1)$，则质心位置坐标为

$$\bar{x}=\frac{1}{mn}\sum _{i=0}^{n-1}\sum _{j=0}^{m-1}{x}_i;\bar{y}=\frac{1}{mn}\sum _{i=0}^{n-1}\sum _{j=0}^{m-1}{y}_j$$

B：方向

方向：如果物体是细长的，则可以把较长方向的轴定为物体的方向。将最小二阶矩轴（最小惯量轴在二维平面上的等效轴）定义为较长物体的方向。也就是说，要找出一条直线，使下式定义的$E$值最小

$$E=\iint r^{2}f(x,y)dxdy$$

C：尺寸

长宽：当物体的边界已知时，用其外接矩形的尺寸来刻画它的基本形状是最简单的方法求物体在坐标系方向上的外接矩形，只需计算物体边界点的最大和最小坐标值，就可得到物体的水平和垂直跨度

• 最小外接矩形：对任意朝向的物体，水平和垂直并非是我们感兴趣的方向。有必要确定物体的主轴，然后计算反映物体形状特征的主轴方向上的长度和与之垂直方向上的宽度，这样的外接矩形是物体的

周长：区域的边界长度，用于区别具有简单或复杂形状的物体；表示方法不同，计算方法也不同

• 边界用隙码表示：把图像中的像素看作单位面积小方块，则图像中的区域和背景均由小方块组成。区域的周长即为区域和背景缝隙的长度和，此时边界用隙码表示。因此，求周长就是计算隙码的长度
• 边界用链码表示：把像素看作一个个点时，周长用链码表示，求周长也即计算链码长度
• 边界用面积表示：即边界点数之和，每个点占面积为1的一个小方块

面积：度量物体的总尺寸，只与该物体的边界有关，与其内部灰度级的变化无关。像素计数面积是指

• 统计边界内部(也包括边界上)的像素数目
• 对二值图像而言，若用1表示物体，用0表示背景，其面积就是统计$f(x,y)=1$的个数

（3）程序

如下：对图像进行阈值分割，并统计区域的几何特征

---

matlab：

clear,clc,close all;
image=imread('plane.jpg');
BW=im2bw(rgb2gray(image));
figure,imshow(BW),title('二值化图像');
% imwrite(BW,'biplane.jpg');
SE=strel('square',3);
Morph=imopen(BW,SE); 
Morph=imclose(Morph,SE);
figure,imshow(Morph),title('形态学滤波'); 
% imwrite(Morph,'morphplane.jpg');
[B,L]=bwboundaries(1-Morph);
figure,imshow(L),title('划分的区域');
% imwrite(L,'Lplane.jpg');
STATS = regionprops(L,'Area', 'Centroid','Orientation','BoundingBox');
figure,imshow(image),title('检测的区域');
hold on;
for i=1:length(B)
    boundary=B{i};
    plot(boundary(:,2),boundary(:,1),'r','LineWidth',2);
end
rectangle('Position',STATS.BoundingBox,'edgecolor','g');
hold off;
% STATS

python：

import numpy as np
import cv2
import matplotlib.pyplot as plt

image = cv2.imread('plane.jpg')
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, bw = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
plt.imshow(bw, cmap='gray')
plt.title('二值化图像')
plt.show()

kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
morph = cv2.morphologyEx(bw, cv2.MORPH_OPEN, kernel)
morph = cv2.morphologyEx(morph, cv2.MORPH_CLOSE, kernel)
plt.imshow(morph, cmap='gray')
plt.title('形态学滤波')
plt.show()

contours, _ = cv2.findContours(255 - morph, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
boundary_image = np.zeros_like(morph)
cv2.drawContours(boundary_image, contours, -1, 255, 1)
plt.imshow(boundary_image, cmap='gray')
plt.title('划分的区域')
plt.show()

stats = []
for contour in contours:
    area = cv2.contourArea(contour)
    centroid = np.mean(contour, axis=0)[0]
    rect = cv2.boundingRect(contour)
    stats.append({
        'Area': area,
        'Centroid': centroid,
        'BoundingBox': rect
    })

image_with_boundary = image.copy()
for boundary in contours:
    cv2.drawContours(image_with_boundary, [boundary], -1, (0, 0, 255), 2)

for stat in stats:
    cv2.rectangle(image_with_boundary, stat['BoundingBox'], (0, 255, 0), 2)

plt.imshow(cv2.cvtColor(image_with_boundary, cv2.COLOR_BGR2RGB))
plt.title('检测的区域')
plt.show()

二：形状描述

（1）矩形度

矩形度：用于描述实体或区域与矩形接近程度的量化指标。它衡量了一个对象或区域在形状上与矩形的相似程度，即其紧凑性和规则性。矩形度是通过比较对象的实际面积和最小外接矩形（Bounding Rectangle）的面积来计算的。最小外接矩形是能够完全包围对象的最小面积的矩形，它的长宽与对象的主要方向一致。矩形度的计算公式如下

• $A_o$：该物体的面积
• $A_{MER}$：MER的面积

$$R=\frac{A_o}{A_{MER}}$$

MER宽与长的比值为

$$r=\frac{W_{MER}}{L_{MER}}$$

（2）圆形度

A：圆度

圆度：用于描述实体或区域与圆形接近程度的量化指标。它衡量了一个对象或区域在形状上与圆形的相似程度，即其圆形度。圆度是通过比较对象的实际面积和等效圆形的面积来计算的。等效圆形是具有与对象相同面积的圆形，其半径可以通过将对象的面积除以π然后开方来计算。圆度的计算公式如下

• $F=1$：区域为圆
• $F<1$：区域为其他形状
• 区域边界弯曲越复杂，区域的性状越偏离圆，F会越小
  $$F=\frac{4\pi A}{P^2}$$

B：边界能量

边界能量：边界上的点的曲率函数

• $P$：物体的周长
• $p$：边界上点到某一起始点的距离
• $r(p)$：边界上一点的瞬时曲率半径。是该点与边界相切圆的半径
• $K(p)$ ：是周期为P的周期函数

$$K(p)=\frac{1}{r(p)}$$

C：圆形性

圆形性：是用于描述实体或物体形状接近球体的度量标准。它衡量了一个对象或区域在形状上与球体的相似程度。圆形性是通过比较对象的体积和等效球体的体积来计算的。等效球体是具有与对象相同体积的球体，其半径可以通过将对象的体积除以(4/3π)然后开立方根来计算

$$\begin{array}{l}C=\frac{{\mu }_R}{{\sigma }_R^2}\\ {\mu }_R=\frac{1}{K}{\sum }_{k=0}^{K-1}\Vert \left(x_k,y_k\right)-(\bar{x},\bar{y})\Vert \\ {\sigma }_R^2=\frac{1}{K}{\sum }_{k=0}^{K-1}{\left[\Vert \left(x_k,y_k\right)-(\bar{x},\bar{y})\Vert -{\mu }_R\right]}^2\end{array}$$

D：内切圆与外接圆半径比

内切圆与外接圆半径比：刻画物体边界的复杂程度

• $r_i$：区域内切圆半径
• $r_c$：区域外接圆半径

$$S=\frac{r_i}{r_c}$$

两个圆的圆心都在区域的重心上

• 当区域为圆时，$S$最大1.0
• 其余形状时，则有$S$＜1.0
• $S$不受区域平移、旋转和尺度变化的影响

E：程序

如下，对原图进行分割，并检测圆和矩形

---

matlab：

clear,clc,close all;
image=rgb2gray(imread('shape.png'));
figure,imshow(image),title('ԭͼ');
BW=edge(image,'canny');
figure,imshow(BW),title('±ß½çͼÏñ');
% imwrite(BW,'shapeedge.jpg');
SE=strel('disk',5); 
Morph=imclose(BW,SE);
figure,imshow(Morph),title('ÐÎ̬ѧÂ˲¨'); 
% imwrite(Morph,'shapemorph.jpg');
Morph=imfill(Morph,'holes');
figure,imshow(Morph),title('ÇøÓòÌî³ä');
imwrite(Morph,'shapefill.jpg');
[B,L]=bwboundaries(Morph);
figure,imshow(L),title('¼ì²âÔ²ºÍ¾ØÐÎ');
% imwrite(L,'Lplane.jpg');
STATS = regionprops(L,'Area', 'Centroid','BoundingBox');
len=length(STATS);
hold on
for i=1:len
    R=STATS(i).Area/(STATS(i).BoundingBox(3)*STATS(i).BoundingBox(4));
    boundary=fliplr(B{i});
    everylen=length(boundary);
    F=4*pi*STATS(i).Area/(everylen^2);
    dis=pdist2(STATS(i).Centroid,boundary,'euclidean');
    miu=sum(dis)/everylen;
    sigma=sum((dis-miu).^2)/everylen;
    C=miu/sigma;
    if R>0.9 && F<1 
        rectangle('Position',STATS(i).BoundingBox,'edgecolor','g','linewidth',2);
        plot(STATS(i).Centroid(1),STATS(i).Centroid(2),'g*');
    end
    if R>pi/4-0.1 && R<pi/4+0.1 && F>0.9 && C>10
        rectangle('Position',[STATS(i).Centroid(1)-miu,STATS(i).Centroid(2)-miu,2*miu,2*miu],...
            'Curvature',[1,1],'edgecolor','r','linewidth',2); 
        plot(STATS(i).Centroid(1),STATS(i).Centroid(2),'r*');
    end
end
hold off

python：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并将其转换为灰度图像
image = cv2.imread('shape.png')
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示原始图片
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('原始图像')
plt.show()

# 边缘检测
edges = cv2.Canny(gray, 30, 100)

# 显示边缘图片
plt.imshow(edges, cmap='gray')
plt.title('边缘图像')
plt.show()

# 闭运算
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5, 5))
closed = cv2.morphologyEx(edges, cv2.MORPH_CLOSE, kernel)

# 显示闭运算结果
plt.imshow(closed, cmap='gray')
plt.title('闭运算')
plt.show()

# 填充内部空洞
filled = cv2.fillHoles(closed)

# 显示填充结果
plt.imshow(filled, cmap='gray')
plt.title('填充后图像')
plt.show()

# 寻找轮廓并进行形状分析
contours, _ = cv2.findContours(filled, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
for cnt in contours:
    area = cv2.contourArea(cnt)
    x, y, w, h = cv2.boundingRect(cnt)
    rect_ratio = area / (w * h)
    perimeter = cv2.arcLength(cnt, True)
    circularity = 4 * np.pi * area / (perimeter ** 2)
    centroid = (int(x + w / 2), int(y + h / 2))
    distance = cv2.pointPolygonTest(cnt, centroid, True)

    if rect_ratio > 0.9 and circularity < 1:
        cv2.rectangle(image, (x, y), (x + w, y + h), (0, 255, 0), 2)
        cv2.circle(image, centroid, 3, (0, 255, 0), -1)

    if np.abs(circularity - np.pi / 4) < 0.1 and rect_ratio > 0.9 and distance > 10:
        cv2.rectangle(image, (int(centroid[0] - distance), int(centroid[1] - distance)),
                      (int(centroid[0] + distance), int(centroid[1] + distance)), (0, 0, 255), 2)
        cv2.circle(image, centroid, 3, (0, 0, 255), -1)

# 显示最终结果
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('形状分析结果')
plt.show()

（3）中轴变换

A：概念

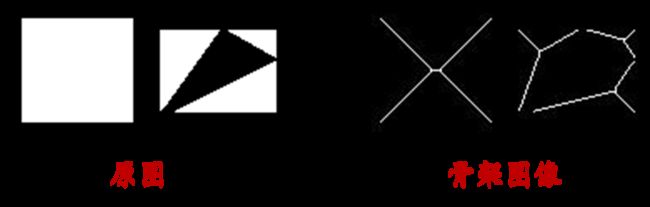
中轴变换：是一种图像处理技术，用于提取对象或区域的中轴线特征。中轴线是指与对象边界相切且具有最大内切圆的曲线。中轴变换的基本思想是通过迭代运算，在对象的边界上逐渐向内部收缩，直到达到中轴线所在位置。在这个过程中，计算每个边界点到最近内切圆的距离，并将这些距离值叠加在一起形成一个距离场。通过阈值处理和连接操作，可以得到中轴线。基本步骤如下

• 对图像进行预处理，例如灰度化、二值化等操作，使得对象与背景分离
• 找到对象的边界，可以使用边缘检测算法（如Canny边缘检测）来获得二值图像的边缘
• 初始化一个空图像作为距离场，距离场的大小与原始图像相同
• 从对象的边界点开始，对每个边界点进行以下操作
  • 计算当前边界点到对象内部的最近内切圆的半径
  • 将该半径值存储在距离场中对应的位置
• 根据距离场的阈值，将其二值化得到中轴图像
• 进行连接操作，对中轴图像进行处理，使得中轴线连续而不间断

中轴变换常用于形状分析、形态学处理、特征提取等领域。通过提取对象的中轴线，可以获得对象的结构信息和几何特征，有助于形状分析、目标识别、图像重建等应用。需要注意的是，中轴变换的结果受到图像预处理、阈值选择、连接方式等因素的影响。因此，在实际应用中，可能需要根据具体情况进行参数调整和优化，以获取更好的中轴线结果

B：程序

如下，提取目标图像骨架

---

matlab：

clear,clc,close all;
Image=imread('test.bmp');
BW=im2bw(Image);
figure,imshow(BW);
result=bwmorph(BW,'skel',Inf);        
figure,imshow(result);

python：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转换为二值图像
image = cv2.imread('test.bmp', 0)
ret, bw = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY)

# 显示原始二值图像
plt.imshow(bw, cmap='gray')
plt.title('原始二值图像')
plt.show()

# 中轴变换
skeleton = np.zeros_like(bw)
size = np.size(bw)
element = cv2.getStructuringElement(cv2.MORPH_CROSS, (3,3))

while True:
    eroded = cv2.erode(bw, element)
    temp = cv2.dilate(eroded, element)
    temp = cv2.subtract(bw, temp)
    skeleton = cv2.bitwise_or(skeleton, temp)
    bw = eroded.copy()

    zeros = size - cv2.countNonZero(bw)
    if zeros == size:
        break

# 显示中轴图像
plt.imshow(skeleton, cmap='gray')
plt.title('中轴图像')
plt.show()