【OpenCV入门】第七部分——图像的几何变换
文章结构
- 缩放
-
- dsize参数实现缩放
- fx参数和fy参数实现缩放
- 翻转
- 仿射变换
-
- 平移
- 旋转
- 倾斜
- 透视
- cmath模块
缩放
通过resize()方法可以随意更改图像的大小比例:
dst = cv2.resize(src, dsize, fx, fy, interpolation)
- src: 原始图像
- dsize: 输出图像的大小,格式为(宽,高),单位为像素
- fx: (可选)水平方向的缩放比例
- fy: (可选)竖直方向的缩放比例
- interpolation: (可选)缩放的插值方式,在图像缩小或放大时需要删减或补充像素,该参数可以指定使用哪种算法对像素进行增减,建议使用默认值
- dst: 缩放之后的图像
resize()方法有两种使用方式,一种时通过dsize参数实现缩放,另一种时通过fx和fy参数实现缩放。
dsize参数实现缩放
dsize参数的格式是一个元组,例如(100,200),表示将图像按照宽100像素、高200像素的大小进行缩放。如果使用dsize参数,就可以不写fx和fy参数。
实例1: 将图像按照指定宽高进行缩放
import cv2
img = cv2.imread("3.png") # 读取图像
dst1 = cv2.resize(img, (100, 100)) # 按照宽100像素、高100像素的大小进行缩放
dst2 = cv2.resize(img, (400, 400)) # 按照宽400像素、高400像素的大小进行缩放
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst1", dst1) # 显示缩放图像
cv2.imshow("dst2", dst2)
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
fx参数和fy参数实现缩放
使用fx参数和fy参数控制缩放时,dsize参数值必须使用None,否则fx和fy会失效。fx参数和fy参数可以使用浮点值,小于1的值表示缩小,大于1的值表示放大。其计算公式为:
- 新图像宽度 = round( fx × 原图像宽度)
- 新图像高度 = round( fy × 原图像高度)
实例2: 将图像按照指定比例进行缩放
import cv2
img = cv2.imread("3.png") # 读取图像
# 将宽缩小到原来的1/3、高缩小到原来的1/2
dst3 = cv2.resize(img, None, fx=1/3, fy=1/2)
dst4 = cv2.resize(img, None, fx=1.5, fy=1.5) # 将宽高扩大1.5倍
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst3", dst3) # 显示缩放图像
cv2.imshow("dst4", dst4) # 显示缩放图像
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
翻转
水平方向被称为X轴,垂直方向被称为Y轴。图像沿着X轴或者Y轴反转之后,可以呈现出镜面倒影的效果。
dst = cv2.flip(src, flipCode)
- src: 原始图像
- flipCode: 翻转类型
- dst: 翻转之后的图像
flipCode参数值及含义:
| 参数值 | 含义 |
|---|---|
| 0 | 沿着X轴翻转 |
| 正数 | 沿着Y轴翻转 |
| 负数 | 同时沿着X轴、Y轴翻转 |
实例3: 同时实现三种翻转效果
import cv2
img = cv2.imread("3.png") # 读取图像
dst1 = cv2.flip(img, 0) # 沿X轴翻转
dst2 = cv2.flip(img, 1) # 沿Y轴翻转
dst3 = cv2.flip(img, -1) # 同时沿X轴、Y轴翻转
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst1", dst1) # 显示翻转之后的图像
cv2.imshow("dst2", dst2)
cv2.imshow("dst3", dst3)
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
仿射变换
仿射变换是一种仅在二维平面中发生的几何变形,变换之后的图像仍然可以保持直线的“平直性”和“平行性”,包含平移、旋转和倾斜。
dst = cv2.warpAffine(src, M, dsize, flags, borderMode, borderValue)
- src: 原始图像。
- M: 一个2行3列的矩阵,根据此矩阵的值变换原图中的像素位置。
- dsize: 输出图像的尺寸大小。
- flags: 可选参数,插值方式,建议使用默认值。
- borderMode: (可选)边界类型,建议使用默认值。
- borderValue: (可选)边界值,默认为0,建议使用默认值返回值说明:
- dst: 经过仿射变换后输出图像
M也被叫作仿射矩阵,实际上就是一个2x3的列表,其格式如下所示:
M = [[a, b, c], [d, e, f]]
图像做何种仿射变换,完全取决于 M 的值,仿射变换输出的图像会按照以下公式进行计算:
- 新x = 原x × a + 原y × b + c
- 新y = 原x × d + 原y × e + f
M矩阵中的数字采用32位浮点格式。可以采用两种方式创建M。
- 创建一个全是0的M
import numpy as np
M = np.zeros((2,3), np.float32)
- 创建M的同时赋予具体值
import numpy as np
M = np.float32([[1, 2 ,3], [4, 5, 6]])
通过设定M的值就可以实现多种仿射效果
平移
平移就是让图像中所有的像素同时沿着水平或垂直方向移动。实现这种效果只需要将M的值按照以下格式进行设置:
M = [[1, 0, 水平移动的距离],[0, 1, 垂直移动的距离]]
原始图像的像素就会按照以下公式进行变换:
- 新x = 原x × 1 + 原y × 0 + 水平移动的距离
- 新y = 原x × 0 + 原y × 1 + 垂直移动的距离
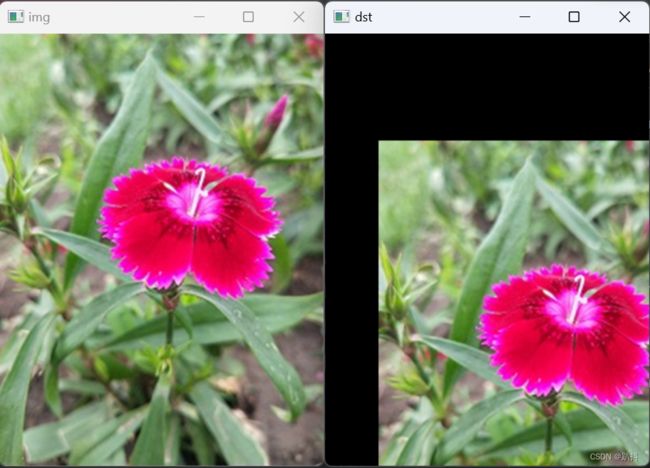
实例4: 让图像向右下方平移
import cv2
import numpy as np
img = cv2.imread("3.png") # 读取图像
rows = len(img) # 图像像素行数
cols = len(img[0]) # 图像像素列数
M = np.float32([[1, 0, 50], # 横坐标向右移动50像素
[0, 1, 100]]) # 纵坐标向下移动100像素
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst", dst) # 显示仿射变换效果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
旋转
让图像旋转也是通过M矩阵实现的,但得出这个矩阵需要做很复杂的计算,于是OpenCV提供了getRotationMatrix2D()方法来自动计算出旋转图像的M矩阵。
M = cv2.getRotationMatrix2D(center, angle, scale)
- center: 旋转的中心点坐标
- angle: 旋转的角度(不是弧度),正数表示逆时针旋转,负数表示顺时针旋转
- scale: 缩放比例,浮点类型,如果取值1,表示图像保持原来的比例
- M: 方法计算出的仿射矩阵
实例5: 让图像逆时针旋转
import cv2
img = cv2.imread("3.png") # 读取图像
rows = len(img) # 图像像素行数
cols = len(img[0]) # 图像像素列数
center = (rows/2, cols/2) # 图像的中心点
# 以图像为中心,逆时针旋转30度,缩放0.8倍
M = cv2.getRotationMatrix2D(center, 30, 0.8)
dst = cv2.warpAffine(img, M, (cols, rows)) # 按照M进行仿射
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst", dst) # 显示仿射变换效果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
倾斜
OpenCV需要定位图像的三个点来计算倾斜效果,三个点的位置如下图所示:

OpenCV会根据这三个点的位置变化来计算其他像素的位置变化。因为要保证图像的“平直性”和“平行性”,所以不需要“右下角”的点做第四个参数,右下角这个点的位置会根据 A、B、C 三点的变化自动计算得出。
让图像倾斜也是需要通过M矩阵实现的,但得出这个矩阵需要做很复杂的运算,于是 OpenCV提供了getAffineTransform()方法来自动计算出倾斜图像的M矩阵。
M = cv2.getAffineTransform(src, dst)
- src: 原图三个点坐标,格式为 3行2列的 32 位浮点数列表,例如: [[0,1] [1,0],[1,1]]
- dst: 倾斜图像的三个点坐标,格式与 src 一样。
- M: 方法计算出的仿射矩阵
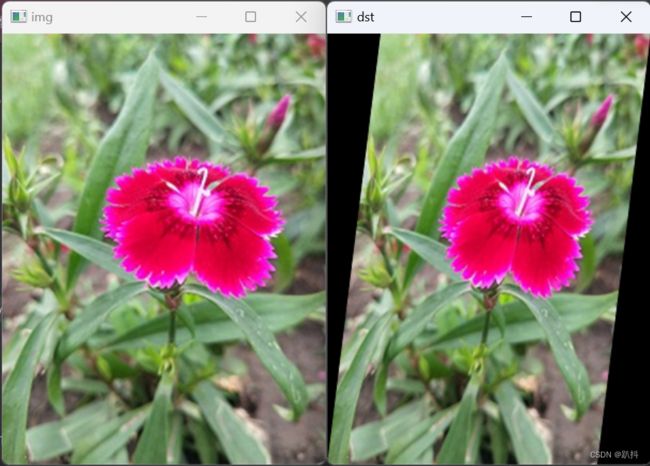
实例6: 让图像向右倾斜
import cv2
import numpy as np
img = cv2.imread("3.png") # 读取图像
rows = len(img) # 图像像素行数
cols = len(img[0]) # 图像像素列数
p1 = np.zeros((3, 2), np.float32) # 32位浮点型空列表,原图三个点
p1[0] = [0, 0] # 左上角点坐标
p1[1] = [cols - 1, 0] # 右上角点坐标
p1[2] = [0, rows - 1] # 左下角点坐标
p2 = np.zeros((3, 2), np.float32) # 32位浮点型空列表,倾斜图三个点
p2[0] = [50, 0] # 左上角点坐标,向右挪50像素
p2[1] = [cols - 1, 0] # 右上角点坐标,位置不变
p2[2] = [0, rows - 1] # 左下角点坐标,位置不变
M = cv2.getAffineTransform(p1, p2) # 根据三个点的变化轨迹计算出M矩阵
dst = cv2.warpAffine(img, M, (cols, rows)) # 按照M进行仿射
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst", dst) # 显示仿射变换效果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
想让图像向左倾斜,不能通过移动A点来实现,需要通过移动B点和C点来实现:
p1 = np.zeros((3, 2), np.float32) # 32位浮点型空列表,原图三个点
p1[0] = [0, 0] # 左上角点坐标
p1[1] = [cols - 1, 0] # 右上角点坐标
p1[2] = [0, rows - 1] # 左下角点坐标
p2 = np.zeros((3, 2), np.float32) # 32位浮点型空列表,倾斜图三个点
p2[0] = [0, 0] # 左上角点坐标,位置不变
p2[1] = [cols - 1 - 50, 0] # 右上角点坐标,向左移动50像素
p2[2] = [50, rows - 1] # 左下角点坐标,向右移动50像素
透视
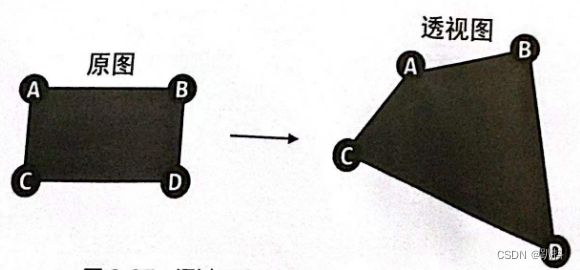
如果说仿射是让图像在二维平面中变形,那么透视就是让图像在三维空间中变形。从不同的角度观察物体,会看到不同的变形画面,例如矩形会变成不规则的四边形、直角会变成锐角或钝角、圆形会变成椭圆等。这种变形之后的画面就是透视图。
如图 8.24 所示从图像的底部去观察图 8.25 的话,图像底部距离眼睛较近,所以宽度不变。但图像顶部距离眼睛较远,宽度就会等比缩小,于是观察者就会看到如图 8.26 所示的透视效果。
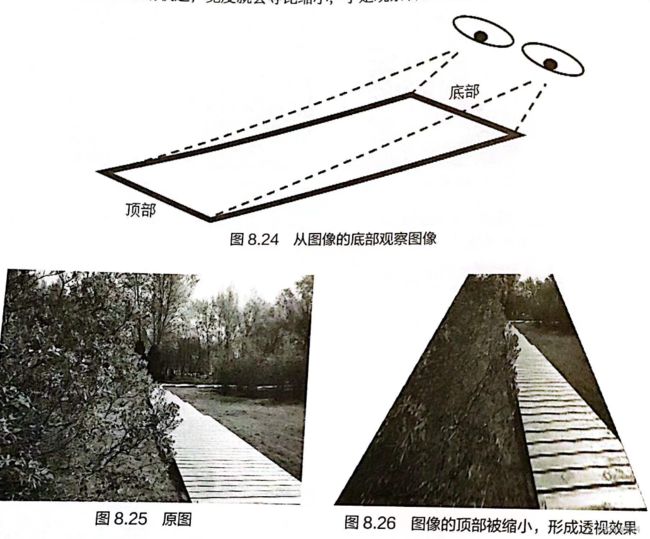
OpenCV中需要通过定位图像的四个点来计算透视效果,四个点的位置如下图所示。OpenCV会根据这四个点的位置变化计算出其他像素的位置变化。透视效果不能保证图像的“平直性”和“平行性”。
dst = cv2.warpPerspective(src, M, dsize, flags, borderMode, borderValue)
- src: 原始图像
- M: 一个3 行 3 列的矩阵,根据此矩阵的值变换原图中的像素位置
- dsize: 输出图像的尺寸大小。
- flags: (可选)插值方式,建议使用默认值。
- borderMode: (可选)边界类型,建议使用默认值。
- borderValue: (可选)边界值,默认为 0,建议使用默认值
- dst: 经过透视变换后输出图像。
warpPerspective() 方法也需要通过 M矩阵来计算透视效果,但得出这个矩阵需要做很复杂的运算,于是OpenCV 提供了getPerspectiveTransform() 方法来自动计算M矩阵。
M = cv2.getPerspectiveTransform(src, dst)
- src: 原图四个点坐标,格式为4行2列的32位浮点数列表,例如[[0,0],[0,1],[1,0][1,1]]
- dst: 透视图的四个点坐标,格式与 src一样
- M: 方法计算出的仿射矩阵
实例7: 模拟从底部观察图像得到的透视效果
import cv2
import numpy as np
img = cv2.imread("demo.png") # 读取图像
rows = len(img) # 图像像素行数
cols = len(img[0]) # 图像像素列数
p1 = np.zeros((4, 2), np.float32) # 32位浮点型空列表,保存原图四个点
p1[0] = [0, 0] # 左上角点坐标
p1[1] = [cols - 1, 0] # 右上角点坐标
p1[2] = [0, rows - 1] # 左下角点坐标
p1[3] = [cols - 1, rows - 1] # 右下角点坐标
p2 = np.zeros((4, 2), np.float32) # 32位浮点型空列表,保存透视图四个点
p2[0] = [90, 0] # 左上角点坐标,向右移动90像素
p2[1] = [cols - 90, 0] # 右上角点坐标,向左移动90像素
p2[2] = [0, rows - 1] # 左下角点坐标,位置不变
p2[3] = [cols - 1, rows - 1] # 右下角点坐标,位置不变
M = cv2.getPerspectiveTransform(p1, p2) # 根据四个点的变化轨迹计算出M矩阵
dst = cv2.warpPerspective(img, M, (cols, rows)) # 按照M进行仿射
cv2.imshow("img", img) # 显示原图
cv2.imshow("dst", dst) # 显示仿射变换效果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
** 实例8:** 生成图书封面俯视图
import cv2
import numpy as np
w, h = 320, 480 # 俯视图的宽高
img = cv2.imread("book.jpg") # 读取原图
tmp = cv2.GaussianBlur(img, (5, 5), 0) # 高斯滤波
tmp = cv2.Canny(tmp, 50, 120) # 变为二值边缘图像
# 闭运算,保证边缘闭合
tmp = cv2.morphologyEx(tmp, cv2.MORPH_CLOSE, (15, 15), iterations=2)
# 检测轮廓
contours, _ = cv2.findContours(tmp, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
for c in contours: # 遍历所有轮廓
area = cv2.contourArea(c) # 计算轮廓面积
if area > 10000: # 只处理面积廓大于10000的轮廓
length = cv2.arcLength(c, True) # 获取轮廓周长
approx = cv2.approxPolyDP(c, 0.02 * length, True) # 计算出轮廓的端点
pts1 = np.float32(approx) # 轮廓四个端点的坐标
pts2 = np.float32([[w, 0], [0, 0], [0, h], [w, h]]) # 正面图对应的四个端点坐标
M = cv2.getPerspectiveTransform(pts1, pts2) # 创建透视图M矩阵
tmp = cv2.warpPerspective(img, M, (w, h)) # 根据M矩阵做透视变换
cv2.imshow("img", img) # 展示原图
cv2.imshow("Top view", tmp) # 展示俯视图
cv2.waitKey() # 按下任何按键后
cv2.destroyAllWindows() # 释放所有窗体
结果如下:
cmath模块
除了前述 OpenCV 提供的用于对图像进行几何变换的方法外,借助 Python 中的 cmath模块也能让图像呈现特定的视觉效果。例如让图像呈现波浪效果等。
通过 Python 中的 cmath 模块就能够让图像呈现波浪效果。cmath 模块提供了数学函数在复数域上扩展的运算函数,这些函数允许复数、整数、浮点数等数据类型的数据输入,因此这些函数的返回值也都是复数。要特别注意的是,组成复数的实部和虚部都是浮点数。
这里要用到的是 cmath 模块中用于返回指定弧度的正弦值的 sin()方法
cmath.sin(x)
- x: 与指定角度对应的弧度
在 cmath 模块中的 sin()方法中,还可以设置与正弦函数对应的正弦图像的振幅和波长。例如把一幅图像的列像素 col 作为弧度,设置与正弦函数对应的正弦图像的振幅为 20、波长为30的关键代码如下所示:
20 * cmath.sin(col/15) # 15是一半的波长
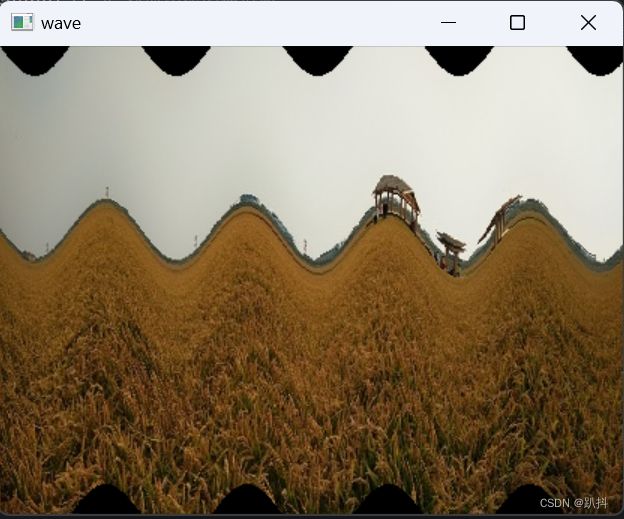
实例9: 呈现波浪效果的图像
import cv2
import numpy as np
import cmath
img = cv2.imread("rice.jpg") # 读取当前项目目录下的图像
shape = img.shape # 获取图像的行像素、列像素和通道数
rows = shape[0] # 获取图像的行像素
columns = shape[1] # 获取图像的列像素
channel = shape[2] # 获取图像的通道数
# 创建了一个行像素与图像的行像素相同,列像素与图像的列像素相同,具有3个通道的画布
canvas = np.zeros([rows, columns, channel], np.uint8)
for row in range(rows): # 遍历图像的行像素
for col in range(columns): # 遍历图像的列像素
# 20是波的振幅,15是一半的波长
# 根据正弦函数计算每个像素点的横坐标移动后的位置
i = row + 20 * cmath.sin(col/15)
i = round(np.real(i)) # 将复数结果转为实数,并四舍五入
if 0 <= i < rows: # 如果移动后的像素点仍在画布范围内
canvas[i, col] = img[row, col] # 将原图像的像素点存放到与画布对应的像素点上
cv2.imshow("wave", canvas) # 在一个名为“wave”的窗口中显示呈现波浪效果的图像
cv2.waitKey() # 通过按下键盘上的按键
cv2.destroyAllWindows() # 销毁正在显示的窗口
结果如下: