【数据结构】 二叉树面试题讲解-＞贰

引言

二叉树的操作算法是笔试面试中较为常见的题目。
本文将着重介绍平时面试中常见的关于二叉树的应用题目，马上要进行秋招了。希望对你们有帮助 _

二叉树遍历

‍题目描述：

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：

输入包括1行字符串，长度不超过100。

输出描述：

可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

‍示例：

输入： abc##de#g##f###
输出：c b e g d f a

‍思路解析：

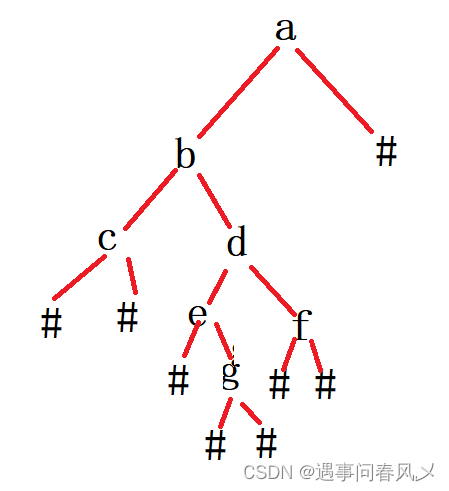
首先我们先来看一下示例输入的二叉树的形状

我们首先需要做的是创建一个二叉树类，用于建立一个新的二叉树

class TreeNode1 {
    char val;
    TreeNode1 left;
    TreeNode1 right;
    TreeNode1() {}
    TreeNode1(char val) {
        this.val = val;
    }
    TreeNode1(char val, TreeNode1 left, TreeNode1 right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

接下来我们需要

• 依旧采用递归的思想
• 对字符串的每一个元素进行遍历，并进行判断
• 在遍历时，我们创建一个静态变量为size，此后每遍历一个元素，size就++
• 若不为’#'，则该结点设为根节点
• 并且size++；
• 然后因为是前序遍历，所以根节点后面应该是左子树，然后是右子树
• 若为’#'，则该节点为null，我们只需要size++即可
• 最后返回该结点就好

代码实现如下：

    public static TreeNode1 creatTree(String str) {
        TreeNode1 root = null;
        if (str.charAt(i) != '#') {
            root = new TreeNode1(str.charAt(i));
            i++;
            root.left = creatTree(str);
            root.right = creatTree(str);
        } else {
            i++;
        }
        return root;
    }

然后根据题意我们还需要进行一个中序遍历，这里我就不做赘述了，又不懂的小伙伴可以去看一下博主对于【数据结构】二叉数的存储与基本操作的实现的讲解

实现如下：

public static void inorder(TreeNode1 root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }
}

‍完整代码实现：

import java.util.Scanner;
class TreeNode1 {
    char val;
    TreeNode1 left;
    TreeNode1 right;
    TreeNode1() {}
    TreeNode1(char val) {
        this.val = val;
    }
    TreeNode1(char val, TreeNode1 left, TreeNode1 right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
public class Main {

    public static int i = 0;
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            i = 0;
            String st = in.nextLine();
            TreeNode1 root = new TreeNode1();
            root = creatTree(st);
            inorder(root);
        }
    }
    public static TreeNode1 creatTree(String str) {
        TreeNode1 root = null;
        if (str.charAt(i) != '#') {
            root = new TreeNode1(str.charAt(i));
            i++;
            root.left = creatTree(str);
            root.right = creatTree(str);
        } else {
            i++;
        }
        return root;
    }
    public static void inorder(TreeNode1 root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }
}

二叉树的最近公共祖先

‍题目描述：

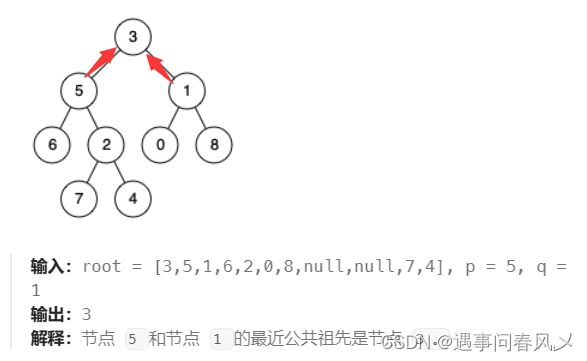
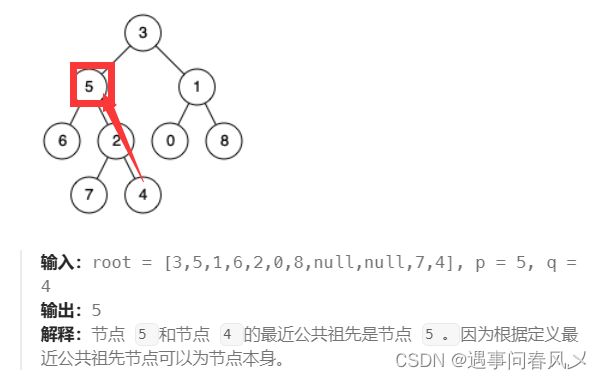
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

    }

‍示例：

示例一

示例二

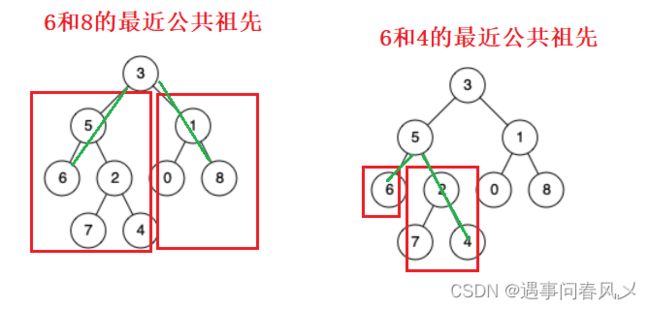
‍思路解析

本题博主提供两种解题思路

思路一

我们发现：

• 如果p，q不是根节点，且p，q一个在左子树被找到，一个在右子树被找到
• 那么该根节点为最近公共祖先
• 
• 若该根节点为p或者q，那么自身则为最近祖先
  
  若最后都没有找到，说明没有，返回空

思路二

我们建立两个栈：

• 栈1用于存储找到p结点的路径
• 栈2用于存储找到q结点的路径
  
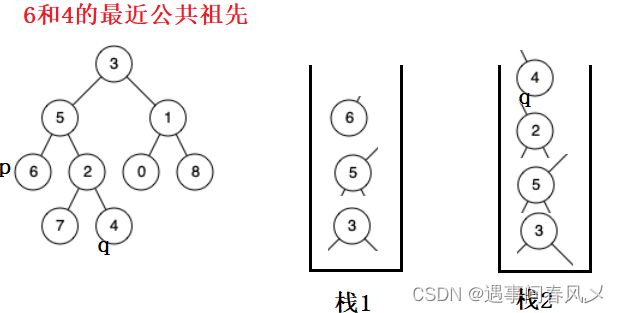
• 然后我们对两个栈求长度，把栈长度比较长的栈进行出栈，直到两个栈长度相等
• 然后同时出栈进行一一比对，相同则为p、q的最近公共祖先
  
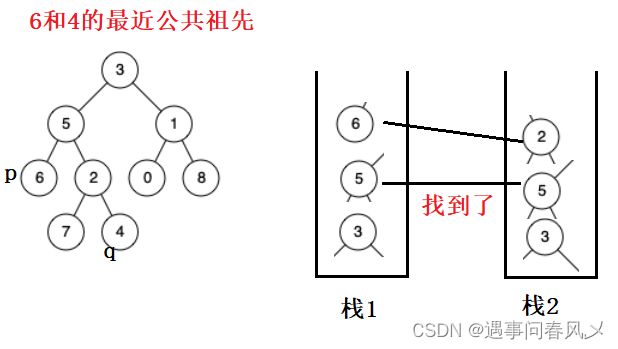
  这种思路的解题难点在于如何找到p、q的路径并放入栈中，博主采用的做法如下：
• 首先我们对二叉树与所找p、q结点进行判断
• 若为空返回false
• 然后我们需要对当前根节点进行判断，若为我们要找的p或q
• 则返回true
• 若没有我们便对该根节点的左子树进行入栈并进行判断，若找到返回true
• 若没有找到则将该左子树进行出栈
• 然后对右子树进行同样操作
• 最后若都没找到，返回false

然后我们只需要对两栈元素进行出栈进行比对就好了，最先相等的就为我们的最近公共祖先

‍代码实现：

思路一代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p == root || q == root) {
            return root;
        }
        if(root == null) {
            return null;
        }
        TreeNode l = lowestCommonAncestor(root.left,p,q);
        TreeNode r = lowestCommonAncestor(root.right,p,q);
        if(l != null && r != null) {
            return root;
        } else if(l != null) {
            return l;
        } else if(r != null) {
            return r;
        }
        return null;
    }
}

思路二代码实现

class Solution {
        public boolean getPath(TreeNode root, TreeNode node,
                           Deque<TreeNode> stack) {
        if(root == null || node == null)return false;
        stack.push(root);
        //放完之后 要检查
        if(root == node) return true;
        boolean ret1 = getPath(root.left,node,stack);
        if(ret1) return true;
        boolean ret2 = getPath(root.right,node,stack);
        if(ret2) return true;
        stack.pop();
        return false;
    }
    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        //1、两个栈当中 存储好数据
        Deque<TreeNode> stack1 = new LinkedList<>();
        getPath(root,p,stack1);
        Deque<TreeNode> stack2 = new LinkedList<>();
        getPath(root,q,stack2);
        //2、判断栈的大小
        int size1 = stack1.size();
        int size2 = stack2.size();
        if(size1 > size2) {
            int size = size1-size2;
            while (size != 0) {
                stack1.pop();
                size--;
            }
        }else {
            int size = size2-size1;
            while (size != 0) {
                stack2.pop();
                size--;
            }
        }
        //栈里面数据的个数 是一样的
        while (!stack1.isEmpty() && !stack2.isEmpty()) {
            if(stack1.peek() != stack2.peek()) {
                stack1.pop();
                stack2.pop();
            }else {
                return stack1.peek();
            }
        }
        return null;
    }
}

从前序与中序遍历序列构造二叉树

‍题目描述

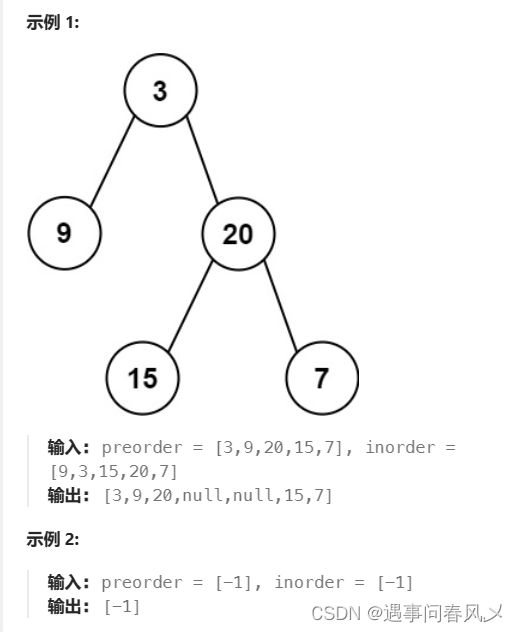
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {

    }
}

‍示例：

‍思路解析：

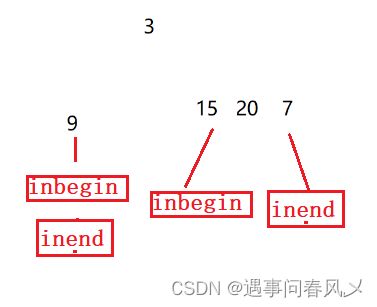
我们知道前序遍历里面第一个存储的是我们的根节点

那我们就可以在我们中序遍历中找到该结点，则该结点两边就为该根节点的左右子树
对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

我们的做法是这样的

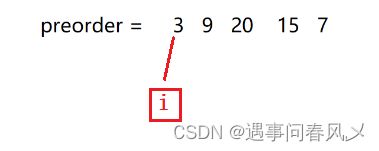
• 我们对前序遍历结果进行下标利用下标 i 遍历，并放入到二叉树中

• 

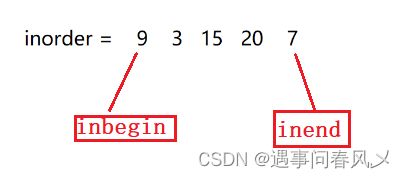
• 对中序遍历的元素设两个下标，一个记录最左边，一个记录最右边

• 

• 对前序遍历里的每一个元素我们会在中序遍历里进行查找，找到后

• 我们的inbegin与inend在左右子树里又会有新的指向

• 

• 然后我们利用递归的思想，对所有元素进行遍历

• 结束条件为inend < inbengin

• 

‍代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int i = 0;
    public TreeNode buildTree(int[] preorder, int[] inorder) {

        return buildTreeChild(preorder,inorder,0,inorder.length-1);
    }

    public TreeNode buildTreeChild(int[] preorder, int[] inorder,
    int inbegin,int inend) {
        if(inbegin > inend) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[i]);
        //找到当前根，在中序遍历的位置
        int rootIndex = findIndex(inorder,inbegin,inend,preorder[i]);
        i++;
        root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);
        root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);
        return root;
    }

    private int findIndex( int[] inorder,int inbegin,int inend, int key) {
        for(int i = inbegin;i <= inend; i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }
}

拓展——从中序与后序遍历序列构造二叉树

与从前序与中序遍历序列构造二叉树实现类似，这里不再做过多赘述

代码实现：

    class Solution2 {
        public int i = 0;
        public TreeNode buildTree(int[] inorder, int[] postorder) {
            i = postorder.length-1;
            return buildTreeChild(postorder,inorder,0,inorder.length-1);
        }

        public TreeNode buildTreeChild(int[] postorder, int[] inorder,
                                       int inbegin,int inend) {
            if(inbegin > inend) {
                return null;
            }
            TreeNode root = new TreeNode(postorder[i]);
            //找到当前根，在中序遍历的位置
            int rootIndex = findIndex(inorder,inbegin,inend,postorder[i]);
            i--;
            root.right = buildTreeChild(postorder,inorder,rootIndex+1,inend);
            root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);
            return root;
        }

        private int findIndex( int[] inorder,int inbegin,int inend, int key) {
            for(int i = inbegin;i <= inend; i++) {
                if(inorder[i] == key) {
                    return i;
                }
            }
            return -1;
        }
    }

⭕总结

关于《【数据结构】 二叉树面试题讲解-＞贰》就讲解到这儿，感谢大家的支持，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下！