c++学习--c++进阶

c++学习

时间复杂度

算法复杂度

算法复杂度分为时间复杂度和空间复杂度。
作用：
时间复杂度是指执行算法所需要的计算工作量。
空间复杂度是指执行这个算法所需要的内存空间。
1.时间复杂度
(1)语法执行次数
算法的语句执行次数，记为T(n)。
算法的实际语句执行次数，记为f(n)。
注：在数值上，T(n)的数量级是小于等于f(n)

(2)时间复杂度
当n趋近于无穷大时，T(n)/f (n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，则称O(f(n)) 为算法的时间复杂度。

时间复杂度计算

一、时间复杂度引入
例如：该算法执行次数为T(n)=2

int main()
{
   cout<<"Hello";//执行1次
   return 0;//执行1次
}

例如：该算法执行次数为T(n)= (1+n + 1 + n + 1) = 2n + 3

int main() {
    int n=100;//执行1次
    for(int i = 0; i<n; i++) {// 执行 (n + 1) 次
        printf("Hello, World!\n");// 执行 n 次
    }
    return 0;// 执行 1 次
}

1、当 T(n) = c，c 为一个常数的时候，记该算法的时间复杂度为 O(1)；如果 T(n) 不等于一个常数项时，直接将常数项省略。
例如：T(n)=n+1 忽略常数项，时间复杂度为O(n)。

2、高次项对于函数的增长速度的影响是最大的。
例如：T(n)=n+n^2 忽略低阶项，时间复杂度为O(n^2)。

3、因为函数的阶数对函数的增长速度的影响是最显著的，所以我们忽略与最高阶相乘的常数。

例如：T(n)=3n^4 忽略最高阶的系数，时间复杂度为O(n^4)。

注意：可根据下图大小关系，可对较小的进行忽略

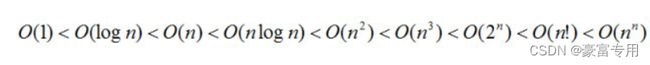
二、时间复杂度计算
1.对于一个循环，循环体的时间复杂度为 O(n)，循环次数为 m，则这个循环的时间复杂度为 O(n×m)。

int main() {
	int n=100;//执行次数为1
    for(int i = 0; i < n; i++) {//循环次数为n
        cout<<"Hello, World!"<<endl;// 循环体时间复杂度为 O(1)
    }
}

此时时间复杂度为 O(1+n × 1)，即 O(n)。

2.对于多个循环，假设循环体的时间复杂度为 O(n)，各个循环的循环次数分别是a, b, c…，则这个循环的时间复杂度为O(n×a×b×c…)。分析的时候应该由里向外分析这些循环。

int main() {
	int n=100;//执行次数为1
    for(int i = 0; i < n; i++) {// 循环次数为 n
        for(int j = 0; j < n; j++) {// 循环次数为 n
            cout<<"Hello, World!"<<endl;// 循环体时间复杂度为 O(1)
        }
    }
}

此时时间复杂度为 O(1+n × n × 1)，即 O(n^2)。

3.对于条件判断语句，总的时间复杂度等于其中时间复杂度最大的路径的时间复杂度。

int main() {
	int n=100;
    if (n >= 0) {
        // 第一条路径时间复杂度为 O(n^2)
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) {
                cout<<"输入数据大于等于零\n"<<endl;
            }
        }
    } else {
        // 第二条路径时间复杂度为 O(n)
        for(int j = 0; j < n; j++) {
            cout<<"输入数据小于零\n"<<endl;
        }
    }
}

此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。

时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数调用，要深入函数进行分析。

时间复杂度的例题：

int s=1;
while(s<n)
{
	s=s*2;
}

每循环一次，s就给自身乘2，乘了x次就跳出循环了。2^x=n，得x=logn。所以O(n)=logn。

二分法

一、快速排序算法模板

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

二、归并排序算法模板

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

三、整数二分算法模板（数的范围）

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

前缀和

定义
前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

一维前缀和

前缀和对算法的优化
例如
输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

可通过遍历区间求和：

const int N = 1e5 + 10;
int a[N];
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
while(m--)
{
    int l, r;
    int sum = 0;
    scanf("%d%d", &l, &r);
    for(int i = l; i <= r; i++)
    { 
        sum += a[i];
    }
    printf("%d\n",sum);
}

注：
1.时间复杂度为O(n * m)，如果n和m的数据量稍微大一点就有可能超时。
2.使用前缀和的方法来做的话就能够将时间复杂度降到O(n + m)，可大大提高了运算效率。

优化的具体做法：

首先做一个预处理，定义一个sum[]数组，sum[i]代表a数组中前i个数的和。

求前缀和运算：

const int N = 1e5 + 10;
int sum[N], a[N]; //sum[i]=a[1]+a[2]+a[3].....a[i];
for(int i = 1;i <= n; i++)
{ 
    sum[i] = sum[i - 1] + a[i];   
}

然后查询操作：

 scanf("%d%d",&l,&r);
 printf("%d\n", sum[r] - sum[l - 1]);

对于每次查询，只需执行sum[r] - sum[l - 1] ，时间复杂度为O(1)

原理图解：

二维前缀和

二维前缀和的结论：
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

原理图解：

前缀和总结：

差分

定义：类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

一维差分

一、差分数组
给定一个原数组a：a[1]， a[2]，a[3]，，， a[n];

构造一个数组b ： b[1]， b[2]， b[3]，，，b[i];

使得 ：a[i] = b[1] + b[2] + b[3] + ，，， + b[i]

a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。每一个a[i]都是b数组中从头开始的一段区间和。

二、构造差分数组

三、一维差分

优化前：
给定区间[l, r ]，让我们把a数组中的[l, r] 区间中的每一个数都加上c,即 a[l] + c , a[l + 1] + c , a[l + 2] + c , a[r] + c;此时的时间复杂度O(n)。

优化后：
使用差分的话只需对差分数组b做 b[l] + = c, b[r+1] - = c 。时间复杂度为O(1), 提高了效率。

总结：
给区间[l,r]中的每个数加上c，只需：b[l] + = c, b[r+1] - = c

二维差分

构建二维差分，可达到与一维差分同等的优化效果，将时间复杂度O(n)优化为O(1)

总结
给(x1,y1)为左上角，(x2,y2)为右下角的子矩阵中所有元素加上c
s[x1][y1] + = c；s[x1,][y2+1] - = c；s[x2+1][y1] - = c；s[x2+1][y2+1] + = c；