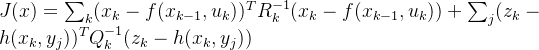VSLAM（3）：最优化问题与优化问题的代码实现

本节总结SLAM问题中的优化问题以及常用数学方法，并且给出图优化问题的定义以及SLAM14讲中的g2o和ceres例子。

目录

一. 最优化问题

1.1 SLAM状态估计问题的定义

1.2 最优化问题

1.3 迭代法解决最优化问题

 1.3.1 梯度下降法

1.3.2 高斯牛顿法（Gassion-Newton）

 1.3.3 阻尼牛顿法LM（Levenberge-Marquadt）

二. 优化问题的代码实现

2.1 曲线拟合问题

 

 

2.3 Ceres

2.3 g2o

参考

一. 最优化问题

1.1 SLAM状态估计问题的定义

最优化问题一般是指求解特定函数定义下的最大值或则最小值，以及此时对应的自变量x的值。在SLAM问题中，可以描述为状态估计问题，这个状态一般是指机器人的位姿，现在定义系统为：

其中是系统的输入，是预测模型的噪声，是观测值，是观测模型的噪声。那么我们就是想在已知系统输入和观测值的条件下去预测x，利用贝叶斯公式可知：

我们假设观测的前后帧是无关的，也就是说当前观测值对应的概率恒为1,那么就可以上面的简化为

然后我们就知道当前观测下的状态变量概率。当这个概率最大时，对应的状态变量x就是我们想要求的最优解。那现在这个状态估计问题就变成了一个最优化问题，即求解使得后验概率最大时对应的状态变量值：

1.2 最优化问题

对于观测，根据观测模型有，假设是一个服从高斯分布的噪声，那么就有

最大化这个函数等于最小化他的相反数，那么对它取负对数，就变成了

最与我们的问题，x对应，而对应，相当于是实际观测量量减去观测模型计算出来的量，最小化噪声值。那么我们就可以定义最优化问题为，求解噪声项的平方最小时，对应的状态变量，因此可以定义代价函数J为：

这个问题就是一个最小二乘问题，一般的解决方法就是对变量分别求偏导，令结果等于0时对应的变量就是我们要的结果。但是对于SLAM问题，求导很复杂，不仅仅是变量可能较多，公式的表达有时候也会很复杂。所以在SLAM中一般是用迭代的方法去找寻最优点。对于优化方法，这篇文有详细的介绍：最优化方法总结——梯度下降法、最速下降法、牛顿法、高斯牛顿法、LM法、拟牛顿法_Dfreedom.的博客-CSDN博客

1.3 迭代法解决最优化问题

迭代法的一般步骤为：

• 给定初始点；
• 确定搜索方向，即按照一定规则，构造 在点处的下降方向作为搜索方向；
• 确定步长因子，使目标函数有某种意义的下降；
• 令 ，若满足某种终止条件，则停止迭代，得到近似最优解.否则，重复以上步骤。

 1.3.1 梯度下降法

对于一个关于x的函数，他在x处的二阶泰勒展开为：

其中J是关于x的Jaccibian矩阵（一阶导数），H则是Hession矩阵（二阶导数）。

如果只考虑一阶项，增量为，那我们只要按照增量的反方向运动，函数一定是递减的，即令

如果按照一定的步长下降，这种算法叫做最速下降法，也叫一阶梯度法。

如果考虑二次项，那么会出现的平方，这就是一个最小二乘问题，那么此时对等式右边求导并等于零得到的就是我们要的最优化值。

那么，这种方法就叫做二次梯度法，也叫牛顿法（Newton）。

1.3.2 高斯牛顿法（Gassion-Newton）

牛顿法需要计算H矩阵，往往导致算法效率偏低，但是快速法的准确率又有问题，可能导致收敛不到最优点。而下面介绍的高斯牛顿法就是用一个矩阵来近似H矩阵，来达到计算效率提升同时准确率高的。

考虑的一次泰勒展开，有

我们将目标换成构建一个最小二乘问题，求解一个一个使得

展开得：

0求导，并令其等于零，就可以得到：

简化为，其中H为增量方程，或称为Gauss Newton equaition or Normal equations。

对比牛顿法可以发现，高斯牛顿法是利用来替代牛顿法中的二阶Hession矩阵，从而省略了计算H的过程。

但是高斯牛顿法存在一些缺点：

1. 要求H可逆，现实中H往往不可逆（半正定或则负定），此时如果继续使用可能会出现H为奇异矩阵或则病态阵，稳定性差，算法不收敛；
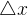2. 过大时会导致局部近似不准，这样无法保证它的迭代收敛。 

 1.3.3 阻尼牛顿法LM（Levenberge-Marquadt）

上面提到的高斯牛顿的缺点第二条，是由于泰勒展开只在展开点的附近生效，距离较远处就无法保证收敛。所以LM法就提出了给添加一个信赖区域（Trust reigon），让他仅在该区域内生效。信赖区域的定义为：

其中分子为实际的改变值，而分母为近似模型下降的值，很小时，说明实际值远小于近似值，近似比较差，需要缩小，反之需要放大。算法流程为

1. 给定初始值，以及初始优化半径，这里是指信赖区域的半径；
2. 对于第k次迭代，求解：
   
3. 计算
4. 若 ，则;
5. 若，则；
6. 如果大于某个阈值，认为近似可行。令;
7. 判断算法是否收敛，如果不收敛则返回2，否则结束循环。

这里的 几个数字都是经验值，对于步骤2中的求解约束下的优化问题，可以使用Langerange乘子把他转换为一个无约束的优化问题。

这里的是朗格朗日乘子，下面时wiki百科对拉格朗日乘子法的介绍，同时放了几个视频讲解有约束最优化问题的链接在参考。拉格朗日乘数https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0将上式的平方项展开后，就可以得到：

这里的H就是在高斯牛顿法中Hassian矩阵，会发现相较于高斯牛顿法多出来一项。D是一个常数矩阵，如果考虑，那么就可以简化为

当较小时，H还是占主导，所以近似看作是高斯牛顿法的下降方法。

二. 优化问题的代码实现

解决优化问题可以通过直接调用现有的优化库实现，14讲中介绍了ceres和g2o这两个优化库。分别使用两个开源库去实现同一个三维线性函数参数估计问题。

2.1 曲线拟合问题

考虑一条满足以下方程的曲线：

其中w表示高斯噪声，满足，abc是需要预测的参数。假设我们现在有N = 100个观测数据，根据这些观测数据区预测模型的参数，这个问题就构成了一个非线性最优化问题：

我们的观测数据时关于y和x的，所以误差的定义就是：

这里如果使用高斯牛顿法去求解，那么根据高斯牛顿法的定义，

需要求解jaccabian矩阵：

下面是参考4中的代码：

#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;

int main(int argc, char **argv) {
	double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
	double ae = 2.0, be = -1.0, ce = 5.0;// 估计参数值
	int N = 100;						 // 数据点
	double w_sigma = 1.0;				 // 噪声Sigma值
	double inv_sigma = 1.0 / w_sigma;
	cv::RNG rng;						 // OpenCV随机数产生器

	Vector x_data, y_data;		 // 数据
	for (int i = 0; i < N;i++) {
		double x = i / 100.0;
		x_data.push_back(x);
		y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
	}

	// 开始Gauss-Newton迭代
	int iterations = 100;				 // 迭代次数
	double cost = 0, lastCost = 0;		 // 本次迭代的cost和上一次迭代的cost

	chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
	for (int iter = 0; iter < iterations; iter++) {
		Matrix3d H = Matrix3d::Zero();   // Hessian = J^T W^{-1} J in Gauss-Newton
		Vector3d b = Vector3d::Zero();	 // bias
		cost = 0;

		for (int i = 0;i < N; i++) {
			double xi = x_data[i], yi = y_data[i]; // 第i个数据点
			double error = yi - exp(ae * xi * xi + be * xi + ce);
			Vector3d J;							   // 雅可比矩阵
			J[0] = - xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da
			J[1] = - xi * exp(ae * xi * xi + be * xi + ce); // de/db
			J[2] = - exp(ae * xi * xi + be * xi + ce); // de/dc

			H += inv_sigma * inv_sigma * J * J.transpose();
			b += - inv_sigma * inv_sigma * error * J;
			cost += error * error;
		}
	   // 求解线性方程 Hx = b
	   Vector3d dx = H.ldlt().solve(b);
	   if (isnan(dx[0])) {
	   		cout << "result is nan!" << endl;
	   		break;
	   }

		if (iter > 0 && cost >= lastCost) {
			cout << "cost: " << cost << ">= last cost:" << lastCost << ",break." << endl;
			break;
		}
		
		ae += dx[0];
		be += dx[1];
		ce += dx[2];

		lastCost = cost;

		cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
		  "\t\testimated params: " << ae << "," << be << "," << ce << endl;
	}	

	chrono::steady_clock::time_point t2 = chrono:;steady_clock::now();
	chrono::duration time_used = chrono:duration_cast>(t2 - t1);
	cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
	cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
	return 0;
}

2.3 Ceres

然后使用ceres库来解决这个问题，下面是ceres库的官网教程：

Non-linear Least Squares — Ceres Solver官方教程

ceres求解最优化问题最一般的形式如下（带边界的核函数最小二乘）：

在这个问题中， 为优化变量，又称参数块（Parameter blocks），称为代价函数（Cost function），也称为残差块（Residual blocks），在SLAM中也可理解为误差项。 和为第个优化变量的上限和下限。在最简单的情况下，取 （不限制优化变量的边界）。此时，目标函数由许多平方项经过一个核函数之后求和组成。同样，可以取为恒等函数，那么目标函数即为许多项的平方和，我们就得到了无约束的最小二乘问题，和先前介绍的理论是一致的。Ceres 使用的一般步骤为：

1. 构造代价函数结构体

2. 通过代价函数构建待求解的优化问题

3. 配置问题并求解问题

下面是具体实现的代码，来源为SLAM14第六章内容

#include 
#include 
#include 
#include 

using namespace std;

// 代价函数的计算模型
struct CURVE_FITTING_COST {
	CUR_FITTING_COST(double x,double y) : _x(x), _y(y) {}

	// 残差的计算
	template
	bool operator()(
		const T *const abc,// 模型参数，有3维
		T *residual) const {
		// y-exp(ax^2+bx+c)
		residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]);
		return true;
	}

	const double _x, _y; // x,y数据
};

int main(int argc,char **argv){
	double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
	double ae = 2.0, be = -1.0, ce = 5.0;// 估计参数值
	int N = 100;						 // 数据点
	double w_sigma = 1.0;				 // 噪声Sigma值
	double inv_sigma = 1.0 / w_sigma;
	cv::RNG rng;						 // OpenCV随机数产生器

	Vector x_data, y_data;		 // 数据
	for (int i = 0; i < N;i++) {
		double x = i / 100.0;
		x_data.push_back(x);
		y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
	}
	
	double abc[3] = {ae, be, ce};

	// 构建最小二乘问题
	ceres::Problem problem;
	for (int i = 0; i < N; i++) {
		problem.AddResidualBlock(	// 向问题中添加误差项
			// 使用自动求导，模板参数:误差类型、输出维度、输入维度，维数要与前面struct中一致
			new ceres::AutoDiffCostFunction(
				new CURVE_FITTING_COST(x_data[i], y_datda[i])
			),
			nullptr,		// 核函数，这里不使用，为空
			abc				// 待估计参数
		);
	}

	// 配置求解器
	ceres::Solver::Options options;								// 这里有很多配置项可以填
	options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;	// 增量方程如何求解
	options.minimizer_progress_to_stdout = true;				// 输出到cout

	ceres::Solver::Summary summary;								// 优化信息
	chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
	ceres::Solve(options, &problem, &summary);					// 开始优化
	chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
	chrono::duration time_used = chrono::duration_cast>(t2 - t1);
	cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

	// 输出结果
	cout << summary.BriefReport() << endl
	cout << "estimated a,b,c = ";
	for (auto a:abc) cout << a << " ";
	cout << endl;

	return 0;
}

2.3 g2o

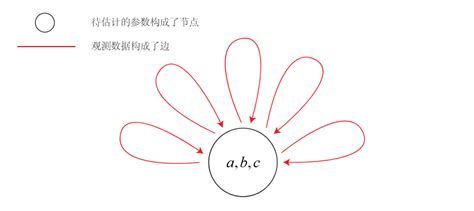
图优化库g2o库全称叫做General Graph Optimization，翻译过来就是通用图优化。首先介绍什么是图优化？图优化，简单的说就是把一个优化问题以图的形式表示出来，并按照通用的方法来解决。图的基本构成有顶点（Vertex）和边（Edge）。每个顶点代表一个我们想要最优化的状态变量，而每个边则一个关于连接顶点的限制条件或则是顶点的关系方程。

边也可以连接一个顶点（Unary Edge，一元边）、两个顶点（Binary Edge，二元边）或多个顶点（Hyper Edge，多元边）。最常见的边连接两个顶点。当一个图中存在连接两个以上顶点的边时，称这个图为超图（Hyper Graph）。而SLAM问题就可以表示成一个超图（在不引起歧义的情况下，后文直接以图指代超图）。

参考6是一篇介绍图优化问题与SLAM问题之间联系的文章。这里是简单介绍g2o库，后面如果找到比较好的基于g2o做的slam问题会另外发一篇文章来介绍。

对于上面2.1介绍的曲线拟合问题，同样可以以图优化的思路来解决。观测数据相当于是一个个表示待估计参数的限制条件，而我们想要估计的参数则是一个顶点，所以以图的形式表示这个问题就如下图所示：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std; 

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    virtual void setToOriginImpl() // 重置
    {
        _estimate << 0,0,0;
    }
    
    virtual void oplusImpl( const double* update ) // 更新
    {
        _estimate += Eigen::Vector3d(update);
    }
    // 存盘和读盘：留空
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

int main( int argc, char** argv )
{
    double a=1.0, b=2.0, c=1.0;         // 真实参数值
    int N=100;                          // 数据点
    double w_sigma=1.0;                 // 噪声Sigma值
    cv::RNG rng;                        // OpenCV随机数产生器
    double abc[3] = {0,0,0};            // abc参数的估计值

    vector x_data, y_data;      // 数据
    
    cout<<"generating data: "< > Block;  // 每个误差项优化变量维度为3，误差值维度为1
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense(); // 线性方程求解器
    Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器
    // 梯度下降方法，从GN, LM, DogLeg 中选
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
    // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
    // g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
    g2o::SparseOptimizer optimizer;     // 图模型
    optimizer.setAlgorithm( solver );   // 设置求解器
    optimizer.setVerbose( true );       // 打开调试输出
    
    // 往图中增加顶点
    CurveFittingVertex* v = new CurveFittingVertex();
    v->setEstimate( Eigen::Vector3d(0,0,0) );
    v->setId(0);
    optimizer.addVertex( v );
    
    // 往图中增加边
    for ( int i=0; isetId(i);
        edge->setVertex( 0, v );                // 设置连接的顶点
        edge->setMeasurement( y_data[i] );      // 观测数值
        edge->setInformation( Eigen::Matrix::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
        optimizer.addEdge( edge );
    }
    
    // 执行优化
    cout<<"start optimization"< time_used = chrono::duration_cast>( t2-t1 );
    cout<<"solve time cost = "<estimate();
    cout<<"estimated model: "<

参考：

1. 最优化总结
2. wiki 拉格朗日乘子
3. SLAM14讲
4. 视觉SLAM十四讲学习记录 第六讲_视觉14讲的第六讲画优化曲线的程序_码农的快乐生活的博客-CSDN博客
5. 一文助你Ceres 入门——Ceres Solver新手向全攻略_福尔摩睿的博客-CSDN博客
6. 深入理解图优化与g2o：图优化篇 - 半闲居士 - 博客园 (cnblogs.com)
7. G2O图优化基础和SLAM的Bundle Adjustment(光束法平差) (zhaoxuhui.top)