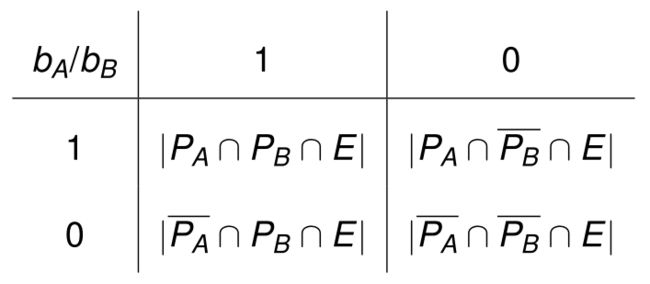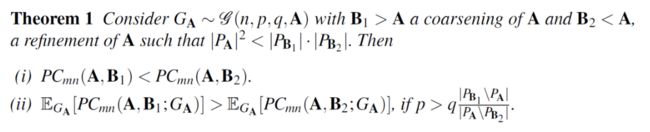【菲尔兹学院夏令营】复杂网络3-社区结构

社区结构

• 图划分（graph partitions）算法比较
• 图聚类算法
• 图上的集成聚类（ECG）

图社区

1. 定义
2. 谱分割
3. Girvan-Newman聚类
4. 基准：种植分区，LFR
5. 模块度
6. 算法

定义

两个基本假设：[Barabasi,Network Science]

1. 一个网络的社区结构在其布局图中是唯一的。
2. 一个社区是网络中的一个局部密集连接子图。

模型：

• 对于一个图$G=(V,E)$，考虑由一个节点$V_C\subset V$的子集诱导的连接子图C（C中的节点满足$i\in V_C$）。

内部外部度：

• 定义节点$i\in V_C$的内部度（其在子图C内的度）：$d_i^{int}(C)$

• 节点i的外部度是：$d_i^{ext}(C)=d_i-d_i^{int}(C)$

  其中$d_i$是节点i在G中的总度

强弱社区：

• 如果对每个节点 $i\in V_C$ ， $d_i^{int}(C)>d_i^{ext}(C)$，则C是一个强社区（strong community）
• 如果对每个节点 $i\in V_C$ ， ${\sum }_{i\in V_C}{d}_i^{\text{int }}(C)>{\sum }_{i\in V_C}{d}_i^{ext}(C)$，则C是一个弱社区（weak community）

集团和核：

• 集团（clique）是G的一个完全连接的子图。
• k核（k-core）是G的一个最大连接子图，其中所有节点的度数至少为k
  • 我们可以通过反复删除所有度数小于k的节点来找到k-cores
  • 如果一个节点属于k-core但不属于(k+1)-core，那么这个节点的核心度（coreness）为k

簇（聚类）：

• 大小为k的图$G=(V,E)$的聚类（clustering）是一个节点$V=V_1\cup ...\cup V_k$的分区，其中：
  • 所有$V_i\cap V_j=\varnothing i\ne j$
  • 对于每个部分（或集群）$V_i$，其诱导子图$G_i$是连通的

谱聚类

谱聚类（Spectral clustering）是一个庞大的话题，本课程只介绍明谱分割（spectral bisection）

参考：

https://blog.csdn.net/weixin_45591044/article/details/122747024

https://blog.csdn.net/SL_World/article/details/104423536

模型：

• 考虑未加权的无向图$G=(V,E)$，邻接矩阵为A

• D是节点度组成的对角矩阵

• $L=D-A$是G的（未归一化的）拉普拉斯系数矩阵

• G中的社群结构与L的特征分解之间关系紧密

• 对于所有的$f\in {\mathbb{R}}^n$：
  $$f^{t}Lf=\frac{1}{2}\sum _{i,j}{a}_{ij}{\left(f_i-f_j\right)}^2$$
  因此，当$a_{ij}>0$时，使上述表达式最小化相当于使$f_i\approx f_j$

求解：

• 考虑比率切分法 ratio-cut ：$V=S\cup S^c$

  与之对应的还有normalized-cut（将拉普拉斯矩阵归一化）

  $$\begin{gathered} \mathrm{Rcut}\left(S,S^c\right)=\frac{\mathrm{Vol}\partial \mathrm{S}}{|S|}+\frac{\mathrm{Vol}\partial \mathrm{S}}{\left|S^c\right|} \\ where\mathrm{Vol}(\partial S)=\left|\left\{e:|E\cap S|=\left|E\cap S^c\right|=1\right\}\right| \end{gathered}$$

  这可以近似求解为：
  $$\underset{f\in {\mathbb{R}}^n}{\min }{f}^{t}Lf;f\perp 1,\Vert f\Vert =\sqrt{n}$$
  其中，结果是对应于L的第二个最小特征值的特征向量——结论推导见参考博客

讨论：

• L是对称的和半正定的，所以所有的特征值都是实数和非负数。

• L有最小的特征值0；这个特征值的倍数对应于G中连接组件的数量。

• 因此，我们可以对这些特征值进行排序，同时对它们各自的特征向量进行排序。

  $0={\lambda }_1\le {\lambda }_2...\le {\lambda }_n$

非连通图情况：

• 有至少两个0特征值
• 按照第二小特征值对应的特征向量，有0和非0两种情况，按这个分类即可。

连通图情况：

• 考虑一个连通图G。它只有一个0特征值。

• 在一个连通图中，特征向量$u_2$对应于费德勒向量中的${\lambda }_2>0$。

• 谱分割是基于费德勒向量（第二小的特征向量）中条目的符号。——正为一类，负为另一类

多个社区：

• 如果有2个以上的聚类，这样的过程可以被递归应用
• 这是一个分裂性层次聚类的例子
• 然而，它可能表现得很糟糕，可能会分割本来存在的社区
• 所以我们去$u_2,...u_k$，再利用k-means等算法对得到的特征向量进行聚类

总结：

一般适用于分组数量已知的情况，核心是最小化割边总和并最大化每个簇的节点数

GN算法

Girvan-Newman算法

步骤：

• 计算每个 $e ∈ E $的边介数，并删除具有最高值的边
• 将生成的图按连通分支拆分（簇）并递归地应用该方法
• 这会产生一个聚类层次结构，我们可以将其表示为树状图

——根据一些标准选择最好的分区，比如模块度（modularity）、或指定集群数量

问题：

• 该算法的一个问题是它的时间复杂度：$O(m^{2}n)$
• 对于非常稀疏的图，也有 $O(n^3) $，仍然很高
• 其他算法可以达到 $O(m)$ 或 $O(nlogn)$

基准

为什么要有社区基准模型？

• 测试和比较算法
• 控制噪音水平、社区规模等
• 真实图数据很少有真实值（ground-truth）
• 有ground-truth，但可能与基本假设不一致

种植-分区模型

Planted partitions model

1. 固定节点数 n 和社区数 k，对于社区，我们：

• 平均分配节点到每个社区

• 或将每个节点独立分配给社区 i，概率为 $p_i$，$\sum p_i=1$

2. 对于分别在社区i和社区j中的节点对$(i,j)$，我们按照概率$P(i,j)$添加边
   • 可以指定$P(i,i)=p_{in}$、$P(i,j)=p_{out},i\ne j$

LFR模型

Lancichinetti-Fortunato-Radicchi model

1. 固定节点数 n

2. 设定三个主要参数：

   1. ${\gamma }_1$：节点度服从 $p_n\propto n^{-{\gamma }_1}$ 的幂律分布；推荐值为 $2\le {\gamma }_1\le 3$。
   2. ${\gamma }_2$：社区规模服从 $p_k\propto k^{-{\gamma }_2}$ 的幂律分布；推荐值为 $1\le {\gamma }_2\le 2$。
   3. $0\le \mu \le 1$：对于每个节点，这是连接到其他社区的边的预期比例，而 $(1-\mu )$ 是其自己社区内的比例。

   ——$\mu$ 称为噪声水平或混合参数

3. 把每个节点都分配到社区

   • 存在允许重叠社区的变体
   • 可以提供额外参数来限制度分布（平均和最大度）和社区大小（最小和最大）
   • 从配置模型开始，重新连接节点以逼近目标分布
   • 初始阶段可以使用BA等其他模型

基准代码生成 3 个文件：

1. 包含节点标记为 1 的边列表的文件
2. 包含节点列表及其社区成员的文件，社区也被标记为 1
3. 具有度分布、社区大小分布和混合参数等统计信息的文件

讨论：

• LFR 的可扩展性有些受限，一些可扩展的基准模型有：

  • RMAT ，生成具有幂律度数分布的图；在 Graph-500 中使用

  • BTER (Block Two-level ER)，生成服从幂律度分布以及社区结构的图

  • SBM（Stochastic Block Model），它也生成具有社区结构的图。

    ——它最简单的定义是种植分区模型的变体。

模块度

引言：

• Barabasi 的第三个基本假设：随机连线的网络缺乏固有的社区结构
• 模块度使用随机连接作为空模型来量化某些图分区的社区结构

模型：

• 考虑无向图 $G=(V,E)$

• 令$|V|=n$, $|E|=m$, $d_i$ 为节点 i 的度数

• 设 $a_{ij}=a_{ji}=1$ 当且仅当 $(i,j)\in E$，否则为 0；设$a_{ii}=2$当且仅当 $(i, i) ∈ E $

• 当我们随机连线时，节点 i 和 j 之间的预期边数（概率）为：
  $$p_{ij}=\frac{d_i{d}_j}{2m}$$

• 令 $V=C_1\cup \cdot \cdot \cdot C_k$，将图划分为 k 个簇。对于某些簇 $C_l$，定义：
  $$q_{C_l}=\frac{1}{2m}\sum _{i,j\in C_l}\left(a_{ij}-p_{ij}\right)$$
  展开为：
  $$q_{C_l}=\frac{{\sum }_{i,j\in C_l}{a}_{ij}}{2m}-\frac{{\sum }_{i,j\in C_l}{d}_i{d}_j}{(2m{)}^2}$$
  令：
  $$e(C_l)=|e\in E;e\subseteq C_l|$$

  $$\mathrm{Vol}\left(C_l\right)=\sum _{i\in C_l}{d}_i$$

  代入可得：
  $$q_{C_l}=\frac{e\left(C_l\right)}{m}-{\left(\frac{\mathrm{Vol}\left(C_l\right)}{2m}\right)}^2$$

• 模块度最终定义为：
  $$q=\sum _{l=1}^k\frac{e\left(C_l\right)}{m}-{\left(\frac{\mathrm{Vol}\left(C_l\right)}{2m}\right)}^2$$

  我们将上面的第一项称为边缘贡献（edge contribution），将第二项称为度税（degree tax）

• 图的模块度 $q^{\ast }(G)$ 有时被定义为所有可能分区中上述指标所取的最大值

讨论（局限）：

• Barabasi 的第四个基本假设：对于一个给定的网络，具有最大模块化的分区对应于最佳社区结构。

• 然而，模块化有一些已知的问题——"最佳 "可能并不总是转化为 “直观”。

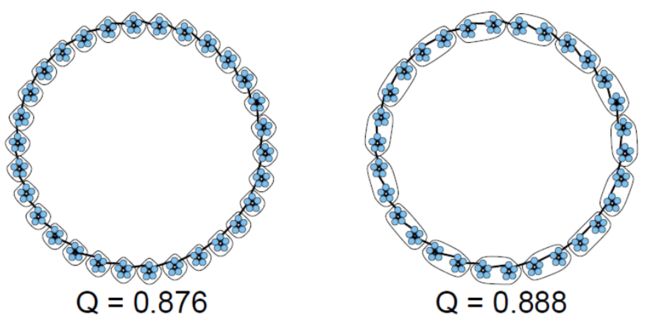
  基于模块化的算法受到分辨率限制问题的影响：

  • 考虑l个大小为m的集团（m-clique）组成的环，$n=l\cdot m$
  • 当$m(m-1)<l-2$时，对相邻的集团进行分组，模块度高于每个集团自己形成集群
  • 正如我们将说明的那样，一些基于模块化的算法因此倾向于对已有社区进行组合

算法

CNM：

CNM算法（Clauset、Newman、Moore），也称为快速贪心算法（Fast Greedy）

• 开始，每个顶点作为一个单独集群
• 选择最能提高模块度的一对集群（如果有的话），然后合并它们
• 当没有办法提高模块度的时候停止
• 复杂度：$O(n^2)$，稀疏图更少

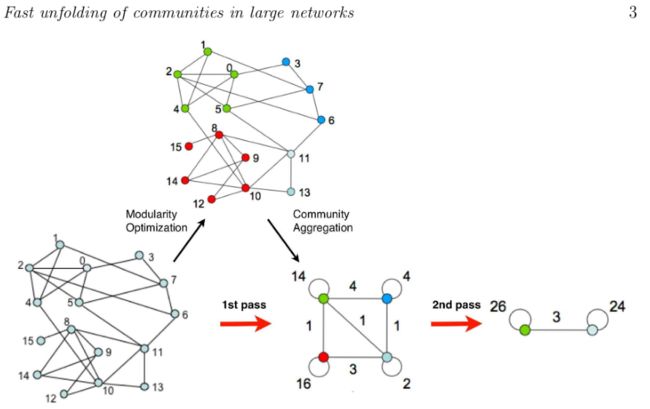
Louvain：

也称为多级算法（Multilevel algorithm）或快速折叠算法（fast unfolding）

• 开始，每个顶点作为一个单独集群
• 循环遍历每个顶点，将其移动到模块度增加最多（如果有的话）的邻居社区
• 重复以上步骤，直到没有任何提升空间为止
• 将每个社区折叠成一个节点并重新运行上述步骤——另一个层级
• 当图折叠到单个节点（或者当最后一级没有移动）时停止
• 复杂度：$O(nlogn)$

Infomap：

• Infomap基于信息论：使用概率随机游走和压缩算法来实现
• 给定 G 和一个初始化分区方案，尽可能高效地编码随机游走
• 利用随机游走往往在同一社区中停留更长时间的性质
• 优化图方程：社区间游走的平均位数+社区内游走的平均位数
• 复杂度：$O(nlogn)$

标签传播：

• 开始，每个顶点作为一个单独集群，有自己的簇标签
• 循环遍历每个顶点，每个顶点都采用其邻居中最流行的标签（使用随机来打破死锁）
• 当每个顶点具有与其邻域中最频繁出现的标签相同的簇标签时，算法停止
• 复杂度：$O(m)$

——注意：此算法速度很快，但并不总能收敛到一个解。

其他：

1. WalkTrap：一种基于短距离随机游走的分层算法。它的复杂度是 $O(n^{2}logn)$。
2. Leading eigenvector（前导特征向量）：基于模块化矩阵的谱分解。对于每个双分区，其复杂度为 $O(n(n+m))$

Louvain和Infomap的算法目前被认为是最先进的。

2023年评论：应该是Leiden算法

图分区的比较（指标）

1. 介绍：图聚类
2. 常见的相似性测度量
3. 与二元分类的联系
4. 图感知度量 （Graph-aware measures）
5. 拓扑学特征

图聚类

符号描述：

$G=(V,E),E\subset V\times V,|V|=n,|E|=m$

• A，邻接矩阵：$a_{ij}=1\iff (i,j)\in E$
• $d_i$：顶点i的程度

术语解释：

• 图聚类/分割（clustering/partitioning）：将顶点分割成相连的子图
• 社区发现（Community finding）：并非所有的顶点都需要被分配到一个群组中去
• 模糊聚类（Fuzzy clustering）：节点不属于、属于一个或多个群组

图划分：$\mathbf{A}=\{A_1,A_2,...,A_k\}$，为节点集$V$的一个划分（partition）

• 每个$A_i$诱导出一个连通子图
• 是连通分支的泛化
  • 集群内的边密度大；集群间的边密度小

应用：

• 图聚类是关系型EDA（互联网数据分析）的一个重要工具

  • 图尺寸缩减
  • 社区检测
  • 异常检测
  • ……

• 如何挑选聚类算法？

  • 集群的质量
  • 稳定性
  • 效率（时间空间）
  • 其他：不需要指定聚类的数量（k）、集群的层次结构等

优化目标：

• 这是无监督学习，所以没有明确的目标函数

• 不同算法使用不同的目标函数：

  1. 模块度：

  $$Q=\frac{1}{2m}\sum _{i,j\in \text{同一簇}}\left(a_{ij}-\frac{d_i{d}_j}{2m}\right)$$

  2. N-cut

  $$\sum _i\frac{\text{ cut }\left(A_i,\overline{A_i}\right)}{\#\text{ edges in }{A}_i}$$

不同分割方法对比：

• 质量的衡量标准：$sim(\mathbf{T},\mathbf{A})\text{w.r.t. ground truth partition}\mathbf{T}$
• 稳定性的衡量标准：同一算法的运行多次比较$sim(\mathbf{A},{\mathbf{A}}^{\prime })$
• 比较算法之间的结果：$sim(\mathbf{A},\mathbf{B})$

相似性

总体分类：

• 基于成对计数（Pairwise-counting）
  $$P{W}_f(\mathbf{A},\mathbf{B})=\frac{\left|P_A\cap P_B\right|}{f\left(\left|P_A\right|,\left|P_B\right|\right)}$$

• 基于信息论
  $$M{I}_f(\mathbf{A},\mathbf{B})=\frac{I(\mathbf{A},\mathbf{B})}{f(H(\mathbf{A}),H(\mathbf{B}))}$$

• 基于卡方分布（${\chi }^2$）
  $$\begin{array}{c}{X}_f^2(\mathbf{A},\mathbf{B})=\frac{X^2(\mathbf{A},\mathbf{B})}{f((k-1),(r-1))}\\ f(x,y)\in \{\min (x,y),\max (x,y),\mathrm{mean}(x,y),\sqrt{xy}\}\end{array}$$

基于成对计数：

• 考虑对图节点的两个划分：

  $\mathbf{A}=(A_1,...,A_k)=(\{1,2,..,7\},\{8\},\cdot \cdot \cdot )$

  $\mathbf{B}=(B_1,...,B_r)=(\{1\},\{2,3,4\},\{5,6,7,8\},\cdot \cdot \cdot )$

• 度量指标基于A和B里面各个集群中的成对元素

  $P_A=\{(1,2),(1,3),(1,4),(1,6),(1,7),(2,3),\cdot \cdot \cdot \}$

  $P_B=\{(2,3),(2,4),(3,4),(5,6),(5,7),(5,8),\cdot \cdot \cdot \}$

• 关键值为：$|P_A\cap P_B|$

• 示例：

  1. Jaccard 指数：
     $$\frac{|P_A\cap P_B|}{|P_A\cup P_B|}$$

  2. 兰德指数

  $$\frac{|P_A\cap P_B|+|\overline{P_A}\cap \overline{P_B}|}{\left(\begin{array}{c}n\\ 2\end{array}\right)}$$

基于信息论：

• 基于 A 和 B 之间的互信息

• 关键值为：
  $$I(\mathbf{A},\mathbf{B})=\sum _{i,j}\frac{\left|A_i\cap B_j\right|}{n}\log \frac{\left|A_i\cap B_j\right|/n}{\left|A_i\right|\left|B_j\right|/n^2}$$

• 示例：归一化互信息 (NMI)：
  $$\frac{I(\mathbf{A},\mathbf{B})}{(H(\mathbf{A})+H(\mathbf{B}))/2}$$

基于卡方分布：

• 关键值为：
  $$X^2(\mathbf{A},\mathbf{B})=\sum _{i,j}\frac{1}{\left|A_i\right|\left|B_j\right|}{\left(\left|A_i\cap B_j\right|-\frac{\left|A_i\right|\left|B_j\right|}{n}\right)}^2$$

• 示例：Cramer 的 V指标 和 Tschurprow 的 T指标

测量指标vs.大小分布：

问题：比较不同大小的分区时，这些度量指标表现怎么样？

实验（多次重复）：

• $\mathbf{A}$：节点V的划分 $|V|=10$
• ${\mathbf{B}}^{(t)}$，V 的随机分区 $|{\mathbf{B}}^{(t)}|=t$，$t=2、5、10、20、30、40、50、100$
• 测量 $\mathbf{A}$ 和所有分区 ${\mathbf{B}}^{(t)}$ 之间的相似性——期望所有相似度都很低

——结果：只有兰德系数变得接近1，其他都随着t的增大减小或趋向0

按概率进行调整：

实现 “在聚类结果随机产生的情况下，指标应该接近零”

$$\text{ Adjusted Similarity }(\mathbf{A},\mathbf{B})=\frac{\mathrm{Similarity}(\mathbf{A},\mathbf{B})-\mathrm{Expected}\mathrm{Sim}\left({\left|A_i\right|}^{\prime }s,{\left|B_j\right|}^{\prime }s\right)}{1-\text{ Expected }\mathrm{Sim}\left({\left|A_i\right|}^{\prime }s,{\left|B_j\right|}^{\prime }s\right)}$$

• 成对计数指标的调整：
  $$AP{W}_f(\mathbf{A},\mathbf{B})=\frac{\left|P_A\cap P_B\right|-\left|P_A\right|\left|P_B\right|/\left(\begin{array}{c}n\\ 2\end{array}\right)}{f\left(\left|P_A\right|,\left|P_B\right|\right)-\left|P_A\right|\left|P_B\right|/\left(\begin{array}{c}n\\ 2\end{array}\right)}$$

• Jaccard 没有已知的调整形式

• 调整兰德指数定义为：
  $$ARI(\mathbf{A},\mathbf{B})=AP{W}_{mean}(\mathbf{A},\mathbf{B})$$

• 基于信息论和基于 ${\chi }^2$ 的也可以针对机会进行调整

• 最常用的有：

  1. ARI：调整兰德系数
  2. AMI：调整互信息

——调整后的指标在随机下都趋近于0

二元划分

我们已经有了对比划分的指标，但我们根本没有考虑图拓扑。

测量相似性时应该考虑边吗？

这就引出了下面要讲的图感知测量，在这之前，要先讲下二元划分

边分类：

• 图分区可以由节点 V 上的集合分区表示

  $\mathbf{A}=(\{1\},\{2,3,4\},\{5,6,7,8\},\{9,10,11\},\{12\})$

• 我们还可以考虑二元边分类（顶点是否在同一簇中）

  $(2,3),(2,4),(3,4),...,(9,10),(9,11),(10,11)\to class1$——两端节点在同一簇的边
  $(1,2),(4,5),(8,10),(11,12)\to class0$——两端节点在不同簇的边

• 更正式地说，对于顶点分区 A，我们定义长度为 m 的二元向量 $b_A$，其中，对于每条边 $e=(i,j)\in E$：
  $$b_{\mathbf{A}}(e)=\{\begin{array}{cc}1& \exists A_k\in \mathbf{A}\mid i,j\in A_k\\ 0& \text{ otherwise. }\end{array}$$

• 更进一步地，可以利用此方法对类别1边子集的边进行搜寻。

二元分类器的评估：

• 考虑 $b_A$ 和 $b_B$，两个二元边分类器。

• 用于比较二元分类器的四个基本计数是：

  

• 对应的各种度量指标如下：
  准确性—— g R : ∣ P A ∩ P B ∩ E ∣ + ∣ P A ‾ ∩ P B ‾ ∩ E ∣ ∣ E ∣ J a c c a r d ——  gJ:  ∣ P A ∩ P B ∩ E ∣ ∣ ( P A ∪ P B ) ∩ E ∣ F 分数 ( β = 1 ) —— g P W m n : ∣ P A ∩ P B ∩ E ∣ 1 2 ( ∣ P A ∩ E ∣ + ∣ P B ∩ E ∣ ) 余弦相似度—— g P W g m n : ∣ P A ∩ P B ∩ E ∣ ∣ P A ∩ E ∣ ∣ P B ∩ E ∣ S i m p s o n —— g P W min ⁡ : ∣ P A ∩ P B ∩ E ∣ min ⁡ { ∣ P A ∩ E ∣ , ∣ P B ∩ E ∣ } B r a u n & B a n q u e t —— g P W max ⁡ : ∣ P A ∩ P B ∩ E ∣ max ⁡ { ∣ P A ∩ E ∣ , ∣ P B ∩ E ∣ } \begin{aligned} 准确性——& \mathrm{gR}: \frac{\left|P_A \cap P_B \cap E\right|+\left|\overline{P_A} \cap \overline{P_B} \cap E\right|}{|E|} \\ Jaccard——& \text { gJ: } \frac{\left|P_A \cap P_B \cap E\right|}{\left|\left(P_A \cup P_B\right) \cap E\right|} \\ F 分数 (β = 1)——& \mathrm{gPW}_{m n}: \frac{\left|P_A \cap P_B \cap E\right|}{\frac{1}{2}\left(\left|P_A \cap E\right|+\left|P_B \cap E\right|\right)} \\ 余弦相似度——& \mathrm{gPW}_{g m n}: \frac{\left|P_A \cap P_B \cap E\right|}{\sqrt{\left|P_A \cap E\right|\left|P_B \cap E\right|}} \\ Simpson——& \mathrm{gPW}_{\min }: \frac{\left|P_A \cap P_B \cap E\right|}{\min \left\{\left|P_A \cap E\right|,\left|P_B \cap E\right|\right\}} \\ Braun\&Banquet——& \mathrm{gPW}_{\max }: \frac{\left|P_A \cap P_B \cap E\right|}{\max \left\{\left|P_A \cap E\right|,\left|P_B \cap E\right|\right\}} \\ & \end{aligned} 准确性——Jaccard——F分数(β=1)——余弦相似度——Simpson——Braun&Banquet——​gR:∣E∣∣PA​∩PB​∩E∣+ ​PA​​∩PB​​∩E ​​ gJ: ∣(PA​∪PB​)∩E∣∣PA​∩PB​∩E∣​gPWmn​:21​(∣PA​∩E∣+∣PB​∩E∣)∣PA​∩PB​∩E∣​gPWgmn​:∣PA​∩E∣∣PB​∩E∣ ​∣PA​∩PB​∩E∣​gPWmin​:min{∣PA​∩E∣,∣PB​∩E∣}∣PA​∩PB​∩E∣​gPWmax​:max{∣PA​∩E∣,∣PB​∩E∣}∣PA​∩PB​∩E∣​​

图感知度量

（调整）图感知度量：

• 上一节的指标可以用二元分类向量的乘积表示：

  $\left|P_A\cap P_B\cap E\right|=|b_A\cdot b_B|$

• 我们提出一系列成对计数的图感知度量指标：（一个是普通、另一个是调整后的）
  $$P{C}_f(\mathbf{A},\mathbf{B};G)=\frac{\left|b_{\mathbf{A}}\cdot b_{\mathbf{B}}\right|}{f\left(\left|b_{\mathbf{A}}\right|,\left|b_{\mathbf{B}}\right|\right))},AP{C}_f(\mathbf{A},\mathbf{B};G)=\frac{\left|b_{\mathbf{A}}\cdot b_{\mathbf{B}}\right|-\frac{|b_{\mathbf{A}}|\cdot |b_{\mathbf{B}}|}{|E|}}{f\left(\left|b_{\mathbf{A}}\right|,\left|b_{\mathbf{B}}\right|\right)-\frac{|b_{\mathbf{A}}|\cdot |b_{\mathbf{B}}|}{|E|}}$$

实验：

• 在LFR模型构建的社区中，调整图感知度量的性能指标都很好
• 不同种类的度量指标的度量效果不同（引子）

补充：

——图感知和图无关度量在解决问题方面具有相反的行为

图无关度量即前面说的普通相似性指标ARI等

• 设 G 的真实社区情况为 A， 并设 B1 和 B2 分别是 A 的粗化和细化

• 在某些情况下，在图无关度量下A更接近B2（细化）；在图感知度量下A更接近B1（粗化）

  • 当使用图无关的度量时，集群的数量更多
  • 图感知度量生成的集群的数量更少

• 这两种指标都获得高值是我们做图聚类所希望的

---

定理的公式化描述：

• 考虑Girvan 和 Newman 模型的变体 G(n, p, q, A)，用于研究具有社区结构的图族
• 图有 n 个顶点，A为分区结果
  • p为随机选择两个节点，其中的边在同一分区内的比例；
  • q为随机选择两个节点，其中的边在不同分区内的比例。

---

拓扑特征

• 验证集群的另一种方法是比较集群的拓扑特征：参考Orman et al.,arXiv:1206.4987

• 示例：对于具有 $n_c$ 个节点和 $m_c$ 个边的社区 $c$——

  • 缩放密度(scaled density)：$n_c\cdot m_c/\left(\begin{array}{c}{n}_c\\ 2\end{array}\right)$

  • 内部传递性(internal transitivity)：$\frac{1}{n_c}{\sum }_{i\in c}\frac{e_c(i)}{\left(\begin{array}{c}{d}_c(i)\\ 2\end{array}\right)}$

    其中 $e_c(i)$ 是 c 中 i 的邻居之间的边数，$d_c(i)$ 是 c 中 i 的度数。

• 可以将特征作为簇大小的函数进行比较——比较聚类算法结果和ground truth的图形相似度

结论

• 使用调整后的基于集合的相似性度量，可以减少度量对分区粒度的偏差，消除随机性
• 图无关（ARI，AMI）和图感知（AGRI）度量是互补的：在评估算法的优越性时应同时使用它们

图的集成聚类（ECG）

1. 共识聚类和 ECG
2. 分辨率和稳定性
3. LFR 图上的研究
4. 一些真实的图示例
5. ECG 权重
6. 在异常检测中的应用

ECG

符号说明：

• 令图 G = (V , E), V = {1, 2, . . . , n}, 为无向图
• 对于每个 e ∈ E，边可以具有权重 w(e) > 0，或者考虑所有 w(e) = 1
• 令 $P_i = {C^1_i , …, C^{l_i}_i} $ 是大小为 $l_i$ 的 V 的一个分区
• 定义指示函数$1_{C_i^j}(v)$，表示 $v\in C_i^j$

图聚类的目标：好的、可扩展的、通用的——注意这是无监督学习

1. 关联强度的度量
2. 聚类的层次结构
3. 不需要或尽量少调整参数

——使用集成学习（Ensemble learning）来实现这些目标：利用生成的多个分区来集成——如何合并多个图分区？

ECG算法：

ECG算法是图的共识聚类算法。步骤是：

1. 生成步骤：来自 Louvain (ML) 算法的 k 个随机的 1级别（level-1） 分区：$P=P_1,...P_k$。
2. 集成步骤：在初始图 G = (V, E) 的重新加权版本上运行 ML。 ECG权重是通过联合获得的。

边 $e=(u,v)\in E$ 的 ECG 权重定义为：
$$W_{\mathcal{P}}(u,v)=\{\begin{array}{lc}{w}_{\ast }+\left(1-w_{\ast }\right)\cdot \left(\frac{{\sum }_{i=1}^k{\alpha }_{P_i}(u,v)}{k}\right),& (u,v)\in 2\text{-core }\\ w_{\ast },& \text{ otherwise }\end{array}$$

• $0<w_{\ast }<1$ 是人工定义的最小权重
• ${\alpha }_{P_i}(u,v)={\sum }_{j=1}^{l_i}{1}_{C_i^j}(u)\cdot 1_{C_i^j}(v)$ 表示是否在 $P_i$ 的簇中共现。

通过示例可以看到，一个社区内的节点间的边在集成后权重变大，集团（clique）内的边尤其明显，而社区间的边集成后权重减小，变得很容易区分

分辨率和稳定性

分辨率：

• 基于模块化的算法存在分辨率限制问题：举例集团组成的环，相邻两个组合后模块度更大
• w* 值较小的 ECG 算法缓解了这个问题
• 使用 level-1的Louvain 作为弱学习器是关键——第一层louvain不会聚合那些环上的边

实验：

• 在广义集团环上ECG算法表现也很好：将ECG和louvain、InfoMap比较，分别考察环上连接集团边数从1增加到5时的表现
• 即使噪音很大，权重仍然很显著：当噪声很大时，同一集团中的边权重仍然显著
• 在LFR生成的社区发现上，ECG算法能够很好地保留原始数量：level1的louvain数量过多，最终的louvain数量过少
• 在上一章的图感知与图无关度量上表现也很好

稳定性：

• Louvain 和其他算法的已知问题：多次重新运行同一个算法会得到不同的结果
• 我们通过运行每个算法两次并应用一些比较措施（例如 ARI）来量化稳定性

实验：

• ECG相比louvain在稳定性方面有了很大的改善
• 实证研究表明，结果对参数的选择不是很敏感（低级聚类次数k和最小权重W*）——不过一般情况下k越大、W*越小效果越好。

LFR 图上的比较研究

• 论文在数千个 LFR 图上比较 8 种算法
• 各种指标水平都是ECG较好
• 本研究只考虑γ1 = 2, γ2 = 1，在不同参数的LFR模型下，ECG大部分情况下都比较好

一些观察结论：

1. InfoMap 在大小相同的小型社区上提供最佳结果
2. ECG 在其他情况下提供最佳结果
3. ECG 的效果始终优于单个 Louvain (ML)

真实网络

1. 足球俱乐部网络

   • ECG和InfoMap都取得了最佳结果

2. YouTube网络

   • 1,134,890 个节点（用户）和 2,987,624 条边（好友关系）
   • 2-core 仅覆盖 41.1% 的顶点
   • 8,385 个社区被声明为用户组，这些社区从拓扑角度来看非常薄弱
   • 只有 12 个合格作为弱社区，外部度与总度的比率低于 0.5 我们将此比率扩展到 0.75（类似于 LFR 图中的 µ）
   • 在图感知度量上ECG比InfoMap略胜一筹

权重

ECG 重新加权有助于提升聚类准确性和稳定性

我们讨论了计算的 ECG 权重的其他一些应用

• 我们定义了一个新的社区强度指数 (CSI)
• 我们展示了如何使用权重来放大种子顶点

社区强度指数CSI：

• 边界（0 和 1）附近的 ECG 权重的双峰分布(bi-modal distribution)表明了强大的社区结构
• 我们提出了一个基于点质量 Wasserstein 距离（推土机距离（Earth Mover’s distance））的简单社区强度指标 (CSI)

定义：

• 对于所有边 $(u,v)\in E$，以及来自 ECG 的 $W_P(u,v)$，我们定义：
  $$CSI=1-2\cdot \frac{1}{|E|}\sum _{(u,v)\in E}\min \left(W_{\mathcal{P}}(u,v),1-W_{\mathcal{P}}(u,v)\right)$$
  使得 $0\le CSI\le 1$

关联强度：

• 从图上直观看出高 ECG 权重表示强关联
• 从经验上比较 ECG 权重和三角形出现次数：正相关关系

我们可以使用 ECG 权重作为自我网络的替代方案来放大种子节点

给定一个种子节点 v：

• 确定它所属的集群
• 删除所有 ECG 权重低于某个阈值 τ 的边
• 放大包含 v 的连通分量
• 增加 τ 可以对其进一步放大

——使用此方法可以很好地保留ground truth里面的真实同社区节点

异常检测

最近提出了CADA（community-aware anomaly detection社团感知异常检测）

CADA：

对于每个节点 $v\in V$，令：

• $N(v)$：v 的邻居数。
• $N_c(v)$： v 属于出现次数最多社区的邻居数（通过图聚类）。

$$CAD{A}_x(v)=\frac{N(v)}{N_c(v)}$$

——$x\in \{IM,ML\}$：即InfoMap算法和Louvain算法

实验：

• 原论文仅在 γ1 = 3、 γ2 = 2 的 LFR 图上验证了他们的算法——生成的是大小均一的小社区

• 我们用 ECG 重新审视了这种方法，并为幂律指数提供了更多值

• 对于每个图，我们添加了 200 个具有与 LFR 中相同的度分布的随机异常节点（随机边）

• ECG算法表现都比较好

  AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值。