2023年智能算法之淘金优化器,MATLAB代码免费获取
今天为大家带来一期淘金优化算法(Gold rush optimizer.,GRO)。
GRO算法是受淘金热启发,模拟了淘金者在淘金热时期如何利用淘金的三个关键概念进行淘金:迁移、协作和淘金。
原理详解
①金矿勘探阶段:
与大多数智能算法相似,就是随机生成一批淘金者:
MF是每个淘金者对应的适应度值
②探矿者的迁移阶段
在发现金矿后,淘金者迁移到那里获取黄金。最富金矿的位置是元启发式算法执行过程中搜索空间的最佳点。由于其确切位置未知,因此使用最佳金矿勘探者的位置来估计最佳金矿的位置,如图所示:
模拟金矿探矿者向金矿的迁移公式为:
③金矿开采
每个淘金者都会在金矿区开采更多的黄金。在数学建模中,每个金矿勘探者的位置都被视为金矿的大致位置。金矿开采的相关数学表达式:
④探矿者之间的合作
④探矿者搬迁
金矿勘探者不断移动,他们决策中的一个关键参数是获取更多的黄金。因此,为了决定探矿者是留在原来的位置还是搬到新的位置,通过评估功能对这两个位置进行比较。在这个过程中,如果目标函数的价值有所提高,金矿勘探者就会更新其位置;否则,它保留在先前的位置,该位置被建模为最小化问题中的方程:
伪代码实现:
什么!看到这里大家有没有感觉该算法与灰狼算法很像!好,作者就与灰狼算法比较一下,看看孰强孰弱!
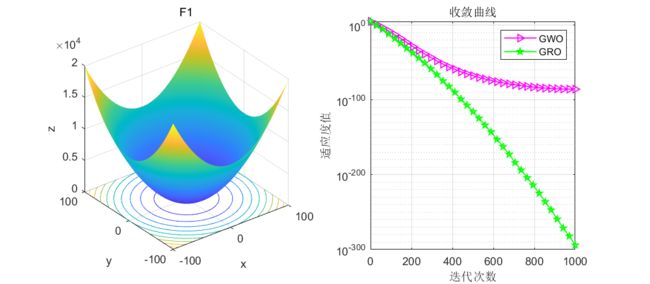
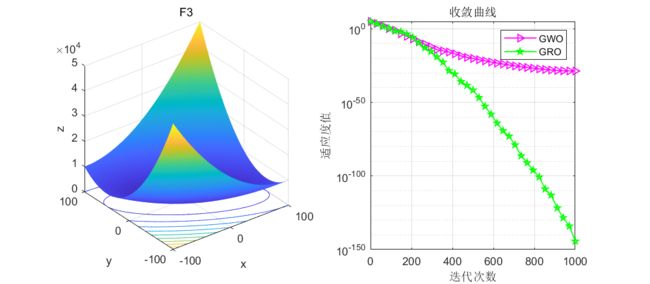
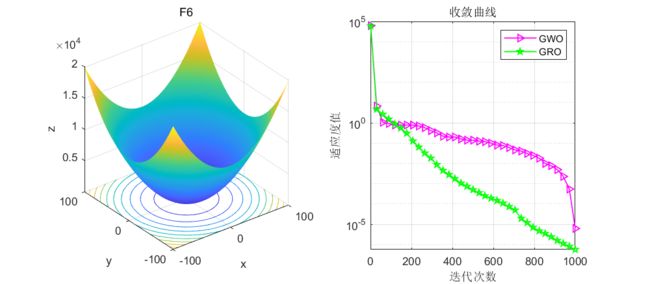
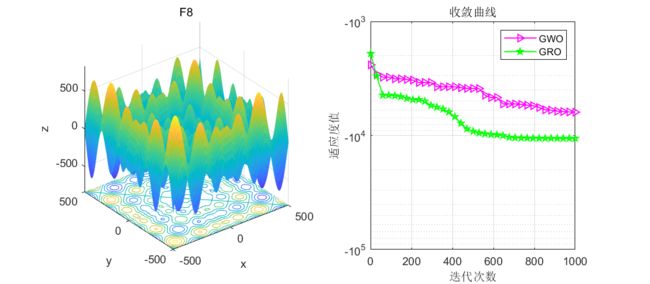
结果展示
在CEC2005函数集进行测试:
GRO是本文的淘金优化器,GWO是灰狼算法
测试了9个函数,不得不说,还是比灰狼算法有很大提升的!且该算法没有增加计算复杂度,因此大家也可以根据此算法的思路去浅浅改进一下灰狼算法,说不定会有质的飞跃!
代码展示
function [best_score,best_pos,Convergence_curve]=GRO(N,Max_iter,lb,ub,dim,fobj )
lb = lb .* ones(1, dim);
ub = ub .* ones(1, dim);
%% GRO parameter initialization
sigma_initial = 2;
sigma_final = 1 / Max_iter ;
% Initialize best position X* (global best)
best_pos=zeros(1, dim);
best_score=inf; %change this to -inf for maximization problems
%Initialize the gold prospectors� population Xi, i = 1, 2, . . . , N
Positions=initialization(N, dim, lb, ub);
Fit = inf(1,N);
%Initialize the gold prospectors� new positions Xnewi = Xi , i = 1, 2, . . . , N
X_NEW = Positions;
Fit_NEW = Fit;
Convergence_curve=zeros(1, Max_iter);
Convergence_curve(1) = min(Fit);
iter = 1;% Loop counter
%% Main loop
while iter <= Max_iter
for i= 1:N
%Calculate fitness of current search agent at new position XNewi
Fit_NEW(i) = fobj(X_NEW(i,:));
%Update position of current search agent Xi according to Equation (13)
if Fit_NEW(i) < Fit(i)
Fit(i) = Fit_NEW(i);
Positions(i,:) = X_NEW(i,:);
end
%Update best search agent X*
if Fit(i) < best_score
% new gold mine is found
best_score = Fit(i);
best_pos = Positions(i,:);
end
end
%Update l1, l2 by Equation (7)
l2 = ((Max_iter - iter)/(Max_iter-1) )^(2 * (sigma_initial - sigma_final)) + sigma_final;
l1 = ((Max_iter - iter)/(Max_iter-1) )^(1 * (sigma_initial - sigma_final)) + sigma_final;
%calculate the next position of current search agent XNewi with one of
%... the migration, mining or collaboration methods
for i = 1:size(Positions,1)
coworkers = randperm(N-1,2);
diggers = 1:N;
diggers(i) = [];
coworkers = diggers(coworkers);
digger1 = coworkers(1); %random prospector g1
digger2 = coworkers(2); %random prospector g2
m = rand;
%collaboration
if m < 1/3
for d = 1:dim
r1 = rand; % r1 is a random number in [0,1]
D3 = Positions(digger2,d) - Positions(digger1,d); % Equation (11)
X_NEW(i,d) = Positions(i,d) + r1 * D3; % Equation (12)
end
%mining method
elseif m < 2/3
for d = 1:dim
r1 = rand; % r1 is a random number in [0,1]
A2 = 2*l2*r1 - l2 ; % Equation (10)
D2 = Positions(i,d) - Positions(digger1,d) ; % Equation (8)
X_NEW(i,d) = Positions(digger1,d) + A2*D2; % Equation (9)
end
%migartion method
else
for d = 1:dim
r1 = rand; % r1 is a random number in [0,1]
r2 = rand; % r2 is a random number in [0,1]
C1 = 2 * r2; % Equation (6)
A1 = 1 + l1 * (r1 - 1/2); % Equation (5)
D1 = C1 * best_pos(d) - Positions(i,d) ; % Equation (3)
X_NEW(i,d) = Positions(i,d) + A1 * D1; % Equation (4)
end
end
%Domain control
X_NEW(i,:) = boundConstraint(X_NEW(i,:),Positions(i,:), lb , ub);
end
Convergence_curve(iter) = best_score;
iter = iter+1;
end
end参考文献:
K. Zolfi. Gold rush optimizer: A new population-based metaheuristic algorithm. Operations Research and Decisions 2023: 33(1), 113-150. DOI 10.37190/ord230108
文献原文已经放在代码压缩包里了。
2023智能算法合集代码免费获取方式
完整代码获取方式:后台回复关键字,不区分大小写。关键字:
2023