操作符&算数转换题
目录
1.交换两个变量(不创建临时变量)
2.统计二进制中1的个数
3.打印整数二进制的奇数位和偶数位
4.求两个数二进制中不同位的个数
5.【一维数组】有序序列合并
6.获得月份天数
7.变种水仙花数
8.选择题总结tips
这篇博文主要分享操作符&算数转换的题目。
1.交换两个变量(不创建临时变量)
2.统计二进制中1的个数
3.打印整数二进制的奇数位和偶数位
4.求两个数二进制中不同位的个数
5.【一维数组】有序序列合并
6.获得月份天数
7.变种水仙花数OJ题目一般有两类
- IO型:输入和输出都是自己写。
- 接口型:只需要完成接口函数就行,剩余的main函数,接口的调用都搞定了。
1.交换两个变量(不创建临时变量)
//题目1
//交换两个变量(不能创建临时变量)
//将数组A中的内容和数组B中的内容进行交换。(数组一样大)//方法1
#include
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
a = a + b;//a=a+b
b = a - b;//a+b-b=a把a的值赋给了b
a = a - b;//a+b-a=b把b的值赋给a
printf("a=%d b=%d", a, b);
return 0;
} //方法2
#include
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
a = a ^ b;
b = a ^ b;//a^b^b=a
a = a ^ b;//a^b^a=b
printf("a=%d b=%d", a, b);
return 0;
} 2.统计二进制中1的个数
//题目2
//统计二进制中1的个数
//输入一个整数 n ,输出该数32位二进制表示中1的个数。其中负数用补码表示。
//写一个函数返回参数二进制中 1 的个数。
//比如: 15 0000 1111 4 个 1
//输入:10
//返回值:2
//说明:十进制中10的32位二进制表示为0000 0000 0000 0000 0000 0000 0000 1010,其中有两个1。
//输入:-1
//返回值:32
//说明:负数使用补码表示 ,-1的32位二进制表示为1111 1111 1111 1111 1111 1111 1111 1111,其中32个1//方法1
// 1234%10=4
// 1234/10=123
// 123%10=3
// 123/10=12
//
// 15%2=1 00000000 00000000 00000000 00001111 1√
// 15/2=7 00000000 00000000 00000000 00000110 7
// 7%2=1 00000000 00000000 00000000 00000110 1√
// 7/2=3 00000000 00000000 00000000 00000011 3
// 3%2=1 00000000 00000000 00000000 00000011 1√
// 3/2=1 00000000 00000000 00000000 00000001 1
// 1%2=1 00000000 00000000 00000000 00000001 1√
// 1/2=0结束循环
#include
//int is_count_1(int n)//但是如果是负数就是错误的❌
int is_count_1(unsigned int n)//搞成无符号的整数就可以输入负数
{
int count = 0;
while (n)//0
{
if (n % 2 == 1)
count++;
n = n / 2;
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret=is_count_1(n);
printf("%d", ret);
return 0;
}
//-1
//10000000 00000000 00000000 00000001_原码
//11111111 11111111 11111111 11111110_反码
//11111111 11111111 11111111 11111111_补码
//无符号
//11111111 11111111 11111111 11111111_原码反码补码均是这个 //方法2
// &有0则为0.同时为1才为1
//((n>>1)&1)得到的是最小位==1则有 ==0则为0
#include
int is_count_1(int n)
{
int count = 0;
int i = 0;
for(i=0;i<32;i++)
{
if (((n >> i) & 1) == 1)
count++;
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = is_count_1(n);
printf("%d", ret);
return 0;
}
//int is_count_1(int n)
//{
// int count = 0;
// while(n)
// {
// if (((n >> 1) & 1) == 1)//死循环不会到达0
// count++;
// }
// return count;
//} 当然还有效率更高的方法
//方法3
//n=n&(n-1)
//15 00000000 00000000 00000000 00001111
//15-1=14 00000000 00000000 00000000 00001110
//15&14 00000000 00000000 00000000 00001110 消除1
//
//15&14 00000000 00000000 00000000 00001110
//15&14-1 00000000 00000000 00000000 00001101
//& 00000000 00000000 00000000 00001100 消除1
// 00000000 00000000 00000000 00001100
//-1 00000000 00000000 00000000 00001011
//& 00000000 00000000 00000000 00001000 消除1
// 00000000 00000000 00000000 00001000
//-1 00000000 00000000 00000000 00001011
//& 00000000 00000000 00000000 00001000 消除1
//计算1的个数等于消除了几个1的个数
//18 00000000 00000000 00000000 00010010
//18-1 00000000 00000000 00000000 00010001
//& 00000000 00000000 00000000 00010000
// 00000000 00000000 00000000 00010000
//-1 00000000 00000000 00000000 00001111
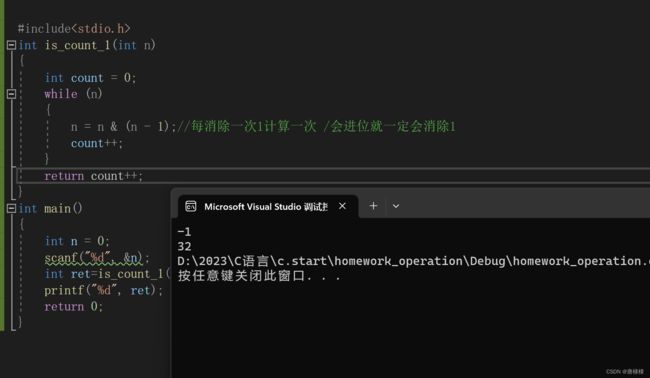
#include
int is_count_1(int n)
{
int count = 0;
while (n)//n!=0的时候进入,当n=0时消除1结束循环结束
{
n = n & (n - 1);//每消除一次1计算一次 /会进位就一定会消除1
count++;
}
return count++;
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret=is_count_1(n);
printf("%d", ret);
return 0;
} 总结
/*
方法一:
思路:
循环进行以下操作,直到n被缩减为0:
1. 用该数据模2,检测其是否能够被2整除
2. 可以:则该数据对应二进制比特位的最低位一定是0,否则是1,如果是1给计数加1
3. 如果n不等于0时,继续1
*/
int NumberOf1(int n)
{
int count = 0;
while(n)
{
if(n%2==1)
count++;
n = n/2;
}
return count;
}
/*
上述方法缺陷:进行了大量的取模以及除法运算,取模和除法运算的效率本来就比较低。
方法二思路:
一个int类型的数据,对应的二进制一共有32个比特位,可以采用位运算的方式一位一位的检测,具体如下
*/
int NumberOf1(unsigned int n)
{
int count = 0;
int i = 0;
for(i=0; i<32; i++)
{
if(((n>>i)&1) == 1)
count++;
}
return count;
}
/*
方法二优点:用位操作代替取模和除法运算,效率稍微比较高
缺陷:不论是什么数据,循环都要执行32次
方法三:
思路:采用相邻的两个数据进行按位与运算
举例:
9999:10 0111 0000 1111
第一次循环:n=9999 n=n&(n-1)=9999&9998= 9998
第二次循环:n=9998 n=n&(n-1)=9998&9997= 9996
第三次循环:n=9996 n=n&(n-1)=9996&9995= 9992
第四次循环:n=9992 n=n&(n-1)=9992&9991= 9984
第五次循环:n=9984 n=n&(n-1)=9984&9983= 9728
第六次循环:n=9728 n=n&(n-1)=9728&9727= 9216
第七次循环:n=9216 n=n&(n-1)=9216&9215= 8192
第八次循环:n=8192 n=n&(n-1)=8192&8191= 0
可以观察下:此种方式,数据的二进制比特位中有几个1,循环就循环几次,而且中间采用了位运算,处理起来比较高效
*/
int NumberOf1(int n)
{
int count = 0;
while(n)
{
n = n&(n-1);
count++;
}
return count;
}3.打印整数二进制的奇数位和偶数位
//题目3
//打印整数二进制的奇数位和偶数位
//获取一个整数二进制序列中所有的偶数位和奇数位,分别打印出二进制序列
//很重要的一个点就是我们可以通过一个方法将二进制所有位
#include
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
for (i = 0; i < 32; i++)
{
if ((n >> i) & 1 == 1)
printf("移动i为时此位的数字:1\n");
if ((n >> i) & 1 == 0)
printf("移动i为时此位的数字:0\n");
}
return 0;
}
//特别注意奇数位和偶数位的是从几开始循环的
//打印二进制序列的奇数位和偶数位
//拿到二进制所有位
//00000000 00000000 00000000 0000000 0
// 偶奇
//32是符号位
/*
思路:
1. 提取所有的奇数位,如果该位是1,输出1,是0则输出0
2. 以同样的方式提取偶数位置
检测n中某一位是0还是1的方式:
1. 将n向右移动i位
2. 将移完位之后的结果与1按位与,如果:
结果是0,则第i个比特位是0
结果是非0,则第i个比特位是1
*/ #include
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
printf("偶数位:");
for (i= 1; i < 32; i+=2)//偶数位
//for(i=31;i>=1;i-=2)//偶数位
{
int t = ((n >> i) & 1);
printf("%d ", t);
}
printf("\n");
printf("奇数位:");
for (i = 0; i < 31; i += 2)//奇数位
//for(i=30;i>=0;i-=2)//奇数位
{
int r = ((n >> i) & 1);
printf("%d ", r);
}
return 0;
} 4.求两个数二进制中不同位的个数
//题目4
//求两个数二进制中不同位的个数
//描述:输入两个整数,求两个整数二进制格式有多少个位不同
//输入描述:两个整数
//输出描述:二进制不同位的个数
//输入:22 33
//输出:5
//编程实现:两个int(32位)整数m和n的二进制表达中,有多少个位(bit)不同?
//1999 2299
//输出例子:7
//方法1还是使用拿到二进制数的所有位来达到题目要求
//方法2
/*
思路:
1. 先将m和n进行按位异或,此时m和n相同的二进制比特位清零,不同的二进制比特位为1
2. 统计异或完成后结果的二进制比特位中有多少个1即可
*///方法1
#include
int main()
{
int m = 0;
int n = 0;
scanf("%d %d", &m, &n);
//输入两个数
int i = 0;
int count = 0;
for (i = 0; i < 32; i++)
{
if (((m >> i) & 1) != ((n >> i) & 1))
count++;
}
printf("%d", count);
return 0;
} //方法2
#include
int main()
{
int m = 0;
int n = 0;
scanf("%d %d", &m, &n);
int r = m ^ n;
//因为异或操作符,对应的二进制位相同为0,相异为1
//m和n的不同的二进制位异或后一定是1
//那我们数一下r的二进制1的个数,就是m和n中不同位的个数
int count = 0;
while (r)
{
//找到r中的1的个数
//这里就可以使用第二题中的三种方法中的任何一种
r = r & (r - 1);
count++;
}
printf("%d", count);
return 0;
} 5.【一维数组】有序序列合并
//题目5
//【一维数组】有序序列合并
//描述:输入两个升序排列的序列,将两个序列合并为一个有序序列并输出。
输入描述:输入包含三行,
第一行包含两个正整数n, m,用空格分隔。n表示第二行第一个升序序列中数字的个数,m表示第三行第二个升序序列中数字的个数。
第二行包含n个整数,用空格分隔。
第三行包含m个整数,用空格分隔。
//输出描述:
输出为一行,输出长度为n+m的升序序列,即长度为n的升序序列和长度为m的升序序列中的元素重新进行升序序列排列合并
//示例
//示例1
输入: 5 6
1 3 7 9 22
2 8 10 17 33 44
输出: 1 2 3 7 8 9 10 17 22 33 44
- 方法1:输入两个数组创建第三个数组,把前两个数组元素全部放入进去,接着再次排序
- 方法2:输入两个数组创建第三个数组(可以不用创建),一边比较大小放入元素一边排序(一边比较大小一边打印)。
//方法1
#include
int main()
{
//放数据到数组里
int m = 0;
int n = 0;
int i = 0;
scanf("%d %d", &m, &n);
int arr1[m];
int arr2[n];
int arr3[m+n];
for (i = 0; i < m; i++)//数组下标从0开始
{
scanf("%d", arr1[i]);
}
for (i = 0; i < n; i++)
{
scanf("%d", arr2[i]);
}
//数据全部放到第三个数组里
for(i=0;im
arr3[i]=arr2[i-m];
}
//冒泡排序
//m+n是arr3里放置的1元素多少,sizeof计算的是arr3全部的大小
for (i = 0; i < m+n; i++)
{
int j = 0;
for (j = 0; j < m+n- i - 1; j++)
{
if (arr3[j] > arr3[j + 1])
{
int tmp = 0;
tmp = arr3[j];
arr3[j] = arr3[j + 1];
arr3[j + 1] = tmp;
}
}
}
for (i = 0; i < m+n; i++)
{
printf("%d ", arr3[i]);
}
return 0;
}
//
#include
#include
int main()
{
//int a, b;
//scanf("%d %d", &a, &b);
//int* p1 = (int*)malloc(a * sizeof(int));
//int* p2 = (int*)malloc(b * sizeof(int));
//int i;
//for (i = 0; i < a; i++)
//{
// p1[i] = scanf("%d", p1 + i);
//}
//for (i = 0; i < b; i++)
//{
// p2[i] = scanf("%d", p2 + i);
//}
//
//合并p2和p3
//int* p3 = (int*)malloc((a + b) * sizeof(int));
//for (i = 0; i < a + b; i++)
//{
// if (i < a)
// p3[i] = p1[i];
// else
// p3[i] = p2[i - a];
//}
int a, b;
scanf("%d %d", &a, &b);
int p1[100] = { 0 };
int p2[100] = { 0 };
int i;
for (i = 0; i < a; i++)
{
scanf("%d", p1+i);
}
for (i = 0; i < b; i++)
{
scanf("%d", p2+i);
}
int p3[200] = { 0 };
for (i = 0; i < a + b; i++)
{
if (i < a)
p3[i] = p1[i];
else
p3[i] = p2[i - a];
}
//冒泡排序
for (i = 0; i < a + b; i++)
{
int j = 0;
for (j = 0; j < a + b - 1 - i; j++)
{
if (p3[j] > p3[j + 1])
{
int tmp = p3[j];
p3[j] = p3[j + 1];
p3[j + 1] = tmp;
}
}
}
//打印
for (i = 0; i < a + b; i++)
{
printf("%d ", p3[i]);
}
return 0;
} 这个方法会产生栈溢出的问题,效率低下,所以使用下面的方法。
关于这种思想和方法,在我们的数据结构中链表中我们也会使用。
经典题目:合并2条有序的链表。
//方法2
//需要变长数组
#include
int main()
{
int n;
int m;
scanf("%d %d", &n, &m);
int arr1[n];
int arr2[m];
int arr3[m+n];
//放数据到数组里
int i = 0;
for (i = 0; i < n; i++)//数组下标从0开始
{
scanf("%d", &arr1[i]);
}
for (i = 0; i //简化
#include
int main()
{
int n = 0;
int m = 0;
int arr1[1000] = {0};
int arr2[1000] = {0};
//输入
scanf("%d %d", &n, &m);
int i = 0;
for(i=0; i 6.获得月份天数
//题目6
//获得月份天数
//描述 KiKi想获得某年某月有多少天,请帮他编程实现。输入年份和月份,计算这一年这个月有多少天。
//输入描述:多组输入,一行有两个整数,分别表示年份和月份,用空格分隔。
//输出描述:针对每组输入,输出为一行,一个整数,表示这一年这个月有多少天。
//示例1
//输入:2008 2
//输出:29
//记住12个月的天数
int m[12] = { 31,28,31,30,31,30,31,31,30,31,30,31 };//平年
int n[12] = { 31,29,31,30,31,30,31,31,30,31,30,31 };//闰年
//数组的下标从0开始,但是我们输入的月数从1开始,所以放入0进去
int m[12] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };//平年
int n[12] = { 0,31,29,31,30,31,30,31,31,30,31,30,31 };//闰年
//表示闰年的方法有两种
//数组直接表示
//平年2月++→闰年//方法1
#include
int is_leap_year(int y)//判断闰年
{
if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0))
return 1;//闰年
else
return 0;//平年
}
int main()
{
int y = 0;
int mouth = 0;
int m[12] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };//平年
int n[12] = { 0,31,29,31,30,31,30,31,31,30,31,30,31 };//闰年
int ret = is_leap_year(y);
while (scanf("%d %d", &y, &mouth) != EOF)
{
if (ret == 1)
{
int k = m[mouth];
printf("%d", k);
}
else
{
int d = n[mouth];
printf("%d", d);
}
}
return 0;
} //方法2
#include
int is_leap_year(int y)//判断闰年
{
if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0))
return 1;//闰年
else
return 0;//平年
}
int main()
{
int y = 0;
int mouth = 0;
int m[12] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };//平年
//int ret = is_leap_year(y);
while (scanf("%d %d", &y, &mouth) != EOF)
{
int day = m[mouth];
//if (ret = 1 && mouth == 2)
if(is_leap_year(y)&&mouth ==2)
{
day++;
}//打印闰年的数组
printf("%d", day);
}
return 0;
}
当然,这里还有一种很特别的思路如下所示
//方法3
#include
int is_leap_year(int y)//判断闰年
{
if ((y % 4 == 0 && y % 100 != 0) || (y % 400 == 0))
return 1;//闰年
else
return 0;//平年
}
int main()
{
int year = 0;
int mouth = 0;
int m[12] = { 31,28,31,30,31,30,31,31,30,31,30,31 };//平年
//int ret = is_leap_year(y);
while (scanf("%d %d", &year, &mouth) != EOF)
{
int day = 0;
//if (ret = 1 && mouth == 2)
if (is_leap_year(year) && mouth == 2)
{
day++;
}//打印闰年的数组
switch (mouth)
{
case 1:
case 3:
case 5:
case 7:
case 8:
case 10:
case 12:
day = 31;
break;
case 4:
case 6:
case 9:
case 11:
day = 30;
break;
case 2:
day = 28;
}
printf("%d", day);
}
return 0;
} 7.变种水仙花数
//题目7
//变种水仙花数
//描述
变种水仙花数 - Lily Number:把任意的数字,从中间拆分成两个数字,
比如1461 可以拆分成(1和461),(14和61),(146和1),如果所有拆分后的乘积之和等于自身,
则是一个Lily Number。
//例如:655 = 6 * 55 + 65 * 5
1461 = 1*461 + 14*61 + 146*1
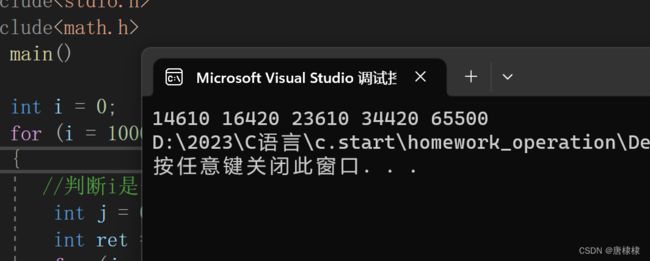
求出 5位数中的所有 Lily Number。
//输入描述:无
//输出描述:一行,5位数中的所有 Lily Number,每两个数之间间隔一个空格。
//水仙花
//12345
//12345/10=1234 12345%10=5 1234和5
//12345/100=123 12345%100=45 123和45
//12345/1000=12 12345%1000=345 12和345
//12345/10000=1 12345%10000=2345 1和2345
//关于/和%#include
#include
int main()
{
int i = 0;
for (i = 10000; i <= 99999; i++)//10000~99999
{
//判断i是否是Lily number
int j = 0;
int ret = 0;
for (j = 1;j<=4;j++)//次方
{
ret = ret + (i /(int) pow (10, j)) * (i %(int) pow(10, j));//整数_数据类型的转化_不能出现小数
}
if (ret == i)
{
printf("%d ", i);
}
}
}
8.选择题总结tips
- 位操作符是二进制位的操作符
- 关于操作符的优先级记忆
#include
int main()
{
int a, b, c;
a = 5;
c = ++a;
b = ++c, c++, ++a, a++;
b += a++ + c;
printf("a = %d b = %d c = %d\n:", a, b, c);
return 0;
} - 赋值类的优先级很低
- 逗号表达式的优先级更低
- ++运算符优先级较高
#include
int main()
{
int a, b, c;
a = 5;
c = ++a;
// ++a:加给a+1,结果为6,用加完之后的结果给c赋值,因此:a = 6 c = 6
b = ++c, c++, ++a, a++;
// 逗号表达式的优先级,最低,这里先算b=++c, b得到的是++c后的结果,b是7
// b=++c 和后边的构成逗号表达式,依次从左向右计算的。
// 表达式结束时,c++和,++a,a++会给a+2,给c加1,此时c:8,a:8,b:7
b += a++ + c;
// a先和c加,结果为16,在加上b的值7,比的结果为23,最后给a加1,a的值为9
printf("a = %d b = %d c = %d\n:", a, b, c);
// a:9, b:23, c:8
return 0;
} - 关于转化的经典题_程序错误
#include
int main()
{
int i = 1;
int ret = (++i)+(++i)+(++i);
printf("ret = %d\n", ret);
return 0;
} 表达式(++i)+(++i)+(++i),只有操作符的优先级和结合性,没法确定唯一计算路径
所以这个表达式可能因为计算顺序的差异导致结果是不一致的,所以表达式是错误的表达式
可以在VS和Linux gcc测试,结果可能有差异。
- 算数转化_数据类型的转化_下面代码的结果是
#include
int i;//0
int main()
{
i--;//-1
if (i > sizeof(i))
{
printf(">\n");
}
else//-1<4
{
printf("<\n");
}
return 0;
}
//一个全局变量,如果不初始化的话,默认初始值为0
相信很多人都会算成> ,但是我们特别注意比较大小的时候,数据的类型是否统一
i=-1是int类型的
sizeof是size_t类型的
需要将i强制转化成size_t类型的(size_t的返回值类型是无符号整型)
也就是-1被当作无符号整数
-1被当作无符号整数的时候,会成为一个非常大的数字
i>sieof(i)
输出大于>- 表达式求值先看是否存在整型提升或算术转换,再进行计算
- 表达式真正计算的时候先看相邻操作符的优先级再决定先算谁
- 相邻操作符的优先级相同的情况下,看操作符的结合性决定计算顺序
- 当然,有了优先级和结合性,表达式也可能有不同的计算路径,导致计算结果的差异
- a^a^b=b
- 二进制中%2 和/2 可以得到想要的位
- 得到二进制中的每一位((n>>i)&1)是1则1,是0则0
- n=n&(n-1)思想
- 数组的下标是从0开始,有符号整型的二进制位的32位是符号位,影响for循环的边界条件
- ^操作符的使用
- 变长数组
- 数组怎样去输入元素
- 循环条件的限制
- 闰年和平年
- %10 %100 %1000——次方
关于以上练习题,大家可以动手写一写。
新学期,祝各位得偿所愿。不要忘记敲代码哦
✔✔✔✔最后,感谢大家的阅读,若有错误和不足,欢迎指正!!
代码----------→【gitee:https://gitee.com/TSQXG】
联系----------→【邮箱:[email protected]】