复杂度分析及五种记号详解(O、Ω、θ、o、ω)
文章目录
- 一、各种渐近记号的概念和区别
-
- O O O和 Ω \Omega Ω
- Θ 或 θ \Theta或\theta Θ或θ
- o o o和 ω \omega ω
- 二、函数比较和运算性质
一、各种渐近记号的概念和区别
我们常用的记号有: O , Ω , Θ ( θ ) , o , ω O,\Omega,\Theta(\theta),o,\omega O,Ω,Θ(θ),o,ω。其中, Θ \Theta Θ和 θ \theta θ是一回事。
O O O和 Ω \Omega Ω
O ( g ( n ) ) = { f ( n ) : 存在正常量 c 和 n 0 , 使得对所有 n ≥ n 0 , 有 0 ≤ f ( n ) ≤ c g ( n ) ) } O(g(n)) = \{f(n):存在正常量c和n_0,使得对所有n\geq n_0 ,有 0\leq f(n) \leq cg(n))\} O(g(n))={f(n):存在正常量c和n0,使得对所有n≥n0,有0≤f(n)≤cg(n))}
Ω ( g ( n ) ) = { f ( n ) : 存在正常量 c 和 n 0 , 使得对所有 n ≥ n 0 , 有 0 ≤ c g ( n ) ≤ f ( n ) ) } \Omega(g(n)) = \{f(n):存在正常量c和n_0,使得对所有n\geq n_0 ,有 0\leq cg(n) \leq f(n))\} Ω(g(n))={f(n):存在正常量c和n0,使得对所有n≥n0,有0≤cg(n)≤f(n))}
(1) 因为对所有的 N ⩾ 1 时有 3 N ⩽ 4 N , 有 3 N = O ( N ) 。 因为对所有的 N \geqslant 1 时有 3 N \leqslant 4 N , 有 3 N = O(N) 。 因为对所有的N⩾1时有3N⩽4N,有3N=O(N)。
(2) 因为当 N ⩾ 1 时有 N + 1024 ⩽ 1025 N , 有 N + 1024 = O ( N ) 。 因为当 N \geqslant 1 时有 N+1024 \leqslant 1025 N , 有 N+1024 = O(N) 。 因为当N⩾1时有N+1024⩽1025N,有N+1024=O(N)。
(3) 因为当 N ⩾ 10 时有 2 N 2 + 11 N − 10 ⩽ 3 N 2 , 有 2 N 2 + 11 N − 10 = O ( N 2 ) 。 因为当N \geqslant 10 时有 2 N^{2}+11 N-10 \leqslant 3 N^{2} , 有 2 N^{2}+11 N-10 = O\left(N^{2}\right) 。 因为当N⩾10时有2N2+11N−10⩽3N2,有2N2+11N−10=O(N2)。
(4) 因为对所有 N ⩾ 1 时有 N 2 ⩽ N 3 , 有 N 2 = O ( N 3 ) 。 因为对所有 N \geqslant 1 时有 N^{2} \leqslant N^{3} , 有 N^{2} = O\left(N^{3}\right) 。 因为对所有N⩾1时有N2⩽N3,有N2=O(N3)。
(5) 作为一个反例 , N 3 ≠ O ( N 2 ) 。因为若不然 , 则存在正的常数 C 和自然数 N 0 , 使得当 N ⩾ N 0 时有 N 3 ⩽ C N 2 , 即 N ⩽ C 。显然 , 当取 N = max { N 0 , ⌊ C ⌋ + 1 } 时这个不等式不成立 , 所以 N 3 ≠ O ( N 2 ) 。 作为一个反例, N^{3} \neq O\left(N^{2}\right) 。因为若不然, 则存在正的常数 C 和自然数 N_{0} , 使得当 N \geqslant N_{0} 时有 N^{3} \leqslant C N^{2} , 即 N \leqslant C 。显然, 当取 N = \max \left\{N_{0},\lfloor C\rfloor+1\right\} 时这个不等式不成立, 所以 N^{3} \neq O\left(N^{2}\right) 。 作为一个反例,N3=O(N2)。因为若不然,则存在正的常数C和自然数N0,使得当N⩾N0时有N3⩽CN2,即N⩽C。显然,当取N=max{N0,⌊C⌋+1}时这个不等式不成立,所以N3=O(N2)。
定理 : f ( n ) = O ( g ( n ) ) 当且仅当 g ( n ) = Ω ( f ( n ) ) f(n)=O(g(n)) \text { 当且仅当 } g(n)=\Omega(f(n)) f(n)=O(g(n)) 当且仅当 g(n)=Ω(f(n))
不难发现,定义中的两队概念一个可以理解为上界,一个是下界,可以颠倒。
比如a比b大,那自然b比a小。所以关于 Ω \Omega Ω的理解直接把 O O O反过来就好。
理解:
1.当我们说“运行时间为 O ( n 2 ) O\left(n^{2}\right) O(n2)”时,意指存在一个 O ( n 2 ) O\left(n^{2}\right) O(n2) 的函数 f ( n ) f(n) f(n) , 使得对 n n n 的任意值, 不管选择什么特定的规模为 n n n 的输人,其运行时间的上界都是 f ( n ) f(n) f(n) 。这也就是说最坏情况运行时间为 O ( n 2 ) O\left(n^{2}\right) O(n2) 。
2.当我们说 f ( n ) = O ( n ) f(n)=O(n) f(n)=O(n),这里的等号不是数学意义上的数值相等,而是集合意义上的 ∈ \in ∈符号的意义,表示 f ( n ) f(n) f(n)属于 O ( n ) O(n) O(n)这个函数集合。所以 f ( n ) = O ( n ) f(n) = O(n) f(n)=O(n)就是 f ( n ) ∈ O ( n ) f(n) \in O(n) f(n)∈O(n)
Θ 或 θ \Theta或\theta Θ或θ
数学定义如下:
Θ ( g ( n ) ) = { f ( n ) : \Theta(g(n)) = \{f(n): Θ(g(n))={f(n):存在正常数 c 1 , c 2 c_1,c_2 c1,c2,和 n 0 n_0 n0,使对于所有的 n ≥ n 0 n \geq n_0 n≥n0,有 0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) } 0 \leq c_1g(n) \leq f(n) \leq c_2g(n)\} 0≤c1g(n)≤f(n)≤c2g(n)}
定理
f ( N ) = θ ( g ( N ) ) f(N)=\theta(g(N)) f(N)=θ(g(N))当且仅当 f ( N ) = O ( g ( n ) ) f(N)=O(g(n)) f(N)=O(g(n))且 f ( N ) = Ω ( g ( N ) ) f(N)=\Omega(g(N)) f(N)=Ω(g(N))。并且这时称 f ( N ) f(N) f(N)与 g ( N ) g(N) g(N)同阶。(有些教科书也把这个定理作为定义)
图示:
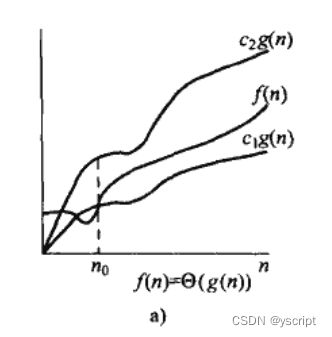
当 n n n充分大时, f ( n ) f(n) f(n)能够被被夹在 c 1 g ( n ) c_1g(n) c1g(n)和 c 2 g ( n ) c_2g(n) c2g(n)之间。我们说 g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的渐进确界。
o o o和 ω \omega ω
o ( g ( n ) ) = { f ( n ) : 对任意正常数 c ,存在常数 n 0 > 0 , 使得对所有 n ≥ n 0 , 有 0 ≤ f ( n ) < c g ( n ) ) } o(g(n)) = \{f(n):对任意正常数c,存在常数n_0>0,使得对所有n \geq n_0 ,有 0\leq f(n) < cg(n))\} o(g(n))={f(n):对任意正常数c,存在常数n0>0,使得对所有n≥n0,有0≤f(n)<cg(n))}(有的书这里是 ≤ \leq ≤,有的是 < < <,不如从极限和无穷小的概念去理解)
参考 O ( g ( n ) ) O(g(n)) O(g(n))的定义:
O ( g ( n ) ) = { f ( n ) : 存在正常量 c 和 n 0 , 使得对所有 n ≥ n 0 , 有 0 ≤ f ( n ) ≤ c g ( n ) ) } O(g(n)) = \{f(n):存在正常量c和n_0,使得对所有n\geq n_0 ,有 0\leq f(n) \leq cg(n))\} O(g(n))={f(n):存在正常量c和n0,使得对所有n≥n0,有0≤f(n)≤cg(n))}
理解:
两者的区别是 O O O提供了渐进上界,但这个界不一定是渐进紧确界。例如 2 n 2 = O ( n 2 ) 2n^2=O(n^2) 2n2=O(n2)是渐进紧确的,但是 2 n = O ( n 2 ) 2n=O(n^2) 2n=O(n2)就不是渐进紧确的,所以我们引入了 o o o记号来专门描述这一部分非渐进紧确的上界集合。




