算法面试问题高频系列(一)
算法面试问题高频系列(一)
算法面试问题高频系列(二)
在面试过程中,一些手撕代码的高频问题值得总结和记录。如:Top K 问题的多种解法、一道结合「简单数据结构 & 简单算法」的面试题、既能考察对「数据结构」的掌握,还能考察对「递归函数」的设计、一道可以考察「二分」本质的面试题
文章目录
-
-
- 一、Top K 问题的多种解法
-
- 703. 数据流中的第 K 大元素
- 1. 冒泡排序法
- 2. 快速排序法
- 3. 优先队列法
- 二、一道结合「简单数据结构 & 简单算法」的面试题
-
- 21. 合并两个有序链表
- 1. 双指针解法(哨兵技巧)
- 2. 递归法实现
- 三、既能考察对「数据结构」的掌握,还能考察对「递归函数」的设计
-
- 24. 两两交换链表中的节点
- 1. 递归解法
- 2. 迭代解法(哨兵技巧)
- 四、一道可以考察「二分」本质的面试题
-
- 33. 搜索旋转排序数组
- 1. 朴素解法
- 2. 二分解法(二次二分)
- 3. 二分解法(一次二分)
- 五、翻转整数
-
- 7. 整数反转
- 1. 不完美解法
- 2. 完美解法
-
一、Top K 问题的多种解法
703. 数据流中的第 K 大元素
leetcode题目链接:703. 数据流中的第 K 大元素
设计一个找到数据流中第 k 大元素的类(class)。注意是排序后的第 k 大元素,不是第 k 个不同的元素。
请实现 KthLargest 类:
KthLargest(int k, int[] nums)使用整数 k 和整数流 nums 初始化对象。int add(int val)将 val 插入数据流 nums 后,返回当前数据流中第 k 大的元素。
示例一:
输入:
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出:
[null, 4, 5, 5, 8, 8]
解释:
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8
提示:
- 1 <= k <= 104
- 0 <= nums.length <= 104
- -104 <= nums[i] <= 104
- -104 <= val <= 104
- 最多调用 add 方法 104 次
- 题目数据保证,在查找第 k 大元素时,数组中至少有 k 个元素
1. 冒泡排序法
每次调用 add 时先将数装入数组,然后遍历 k 次,通过找 k 次最大值来找到 Top K。
但冒泡排序会导致超时。
class KthLargest {
// 冒泡排序
int k;
List<Integer> list = new ArrayList<>(10009);
public KthLargest(int k, int[] nums) {
this.k = k;
for (int i : nums) {
list.add(i);
}
}
public int add(int val) { // 冒泡排序
list.add(val);
int cur = 0;
for (int i = 0; i < k; i++) { // 遍历k次,通过找k次最大值找到Top K
int idx = findMax(cur, list.size() - 1);
swap(cur++, idx);
}
return list.get(cur - 1);
}
int findMax(int start, int end) {
int ans = 0, max = Integer.MIN_VALUE;
for (int i = start; i <= end; i++) {
int t = list.get(i);
if (t > max) {
max = t;
ans = i;
}
}
return ans;
}
void swap(int a, int b) {
int c = list.get(a);
list.set(a, list.get(b));
list.set(b, c);
}
}
2. 快速排序法
上述的解法时间复杂度是 O(nk) 的,当 k 很大的时候会超时。
我们可以使用快排来代替冒泡。
class KthLargest {
// 快排
int k;
List<Integer> list = new ArrayList<>(10009);
public KthLargest(int k, int[] nums) {
this.k = k;
for (int i : nums) {
list.add(i);
}
}
public int add(int val) {
list.add(val);
Collections.sort(list);
return list.get(list.size() - k);
}
}
Collections.sort 内部最终会调用 Arrays.sort 进行排序。而 Arrays.sort() 本身不只有「双轴快排」一种实现,在排序数量少的情况下会直接使用「冒泡排序」,这里的分析是假定了 Collections.sort 最终使用的是 Arrays.sort 的「双轴快排」。
3. 优先队列法
使用优先队列构建一个容量为 k 的小根堆。
将 nums 中的前 k 项放入优先队列(此时堆顶元素为前 k 项的最大值)。
随后逐项加入优先队列:
- 堆内元素个数达到 k 个:
- 加入项小于等于堆顶元素:加入项排在第 k 大元素的后面。直接忽略
- 加入项大于堆顶元素:将堆顶元素弹出,加入项加入优先队列,调整堆
- 堆内元素个数不足 k 个,将加入项加入优先队列
将堆顶元素进行返回(数据保证返回答案时,堆内必然有 k 个元素)。
class KthLargest {
// 优先队列
int k;
PriorityQueue<Integer> queue;
public KthLargest(int k, int[] nums) {
this.k = k;
queue = new PriorityQueue<>(k, (a,b)->Integer.compare(a,b)); // 小根堆
for (int i = 0; i < nums.length && i < k; i++) {
queue.add(nums[i]);
}
for (int i = k; i < nums.length; i++) {
add(nums[i]);
}
}
public int add(int val) {
int t = !queue.isEmpty() ? queue.peek() : Integer.MIN_VALUE;
if (val > t || queue.size() < k) { // 加入项大于堆顶元素,将堆顶元素弹出
if (!queue.isEmpty() && queue.size() >= k) {
queue.poll();
}
queue.add(val); // 加入项加入优先队列,调整堆
}
return queue.peek(); // 堆顶元素就是第K大元素
}
}
1. 为什么使用小根堆?
- 因为我们需要在堆中保留数据流中的前 K 大元素,使用小根堆能保证每次调用堆的 pop()函数时,从堆中删除的是堆中的最小的元素(堆顶)。
2. 为什么能保证堆顶元素是第 K 大元素?
- 因为小根堆中保留的一直是堆中的前 K 大的元素,堆的大小是 K,所以堆顶元素是第 K 大元素。
3. 每次 add() 的时间复杂度是多少?
- 每次 add() 时,调用了堆的 push() 和 pop() 方法,两个操作的时间复杂度都是 log(K).
参考:
面试题警告:经典 TopK ,本题需要重点学习
【面试高频系列】Top K 问题的多种解法:冒泡排序 & 快速排序 & 优先队列
二、一道结合「简单数据结构 & 简单算法」的面试题
21. 合并两个有序链表
leetcode题目链接:21. 合并两个有序链表
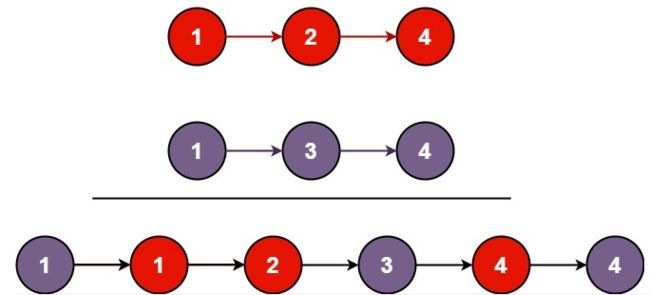
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
1. 双指针解法(哨兵技巧)
做有关链表的题目,有个常用技巧:添加一个虚拟头结点(哨兵),帮助简化边界情况的判断。
由于两条链表本身就是有序的,只需要在遍历过程中进行比较即可:
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
// 1. 双指针,类似于归并排序中的合并过程
// 虚拟头节点
ListNode dummy = new ListNode(0);
ListNode cur = dummy;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
cur.next = list1;
cur = cur.next;
list1 = list1.next;
} else {
cur.next = list2;
cur = cur.next;
list2 = list2.next;
}
}
if (list1 == null) cur.next = list2;
if (list2 == null) cur.next = list1;
return dummy.next;
}
}
2. 递归法实现
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
// 递归
if (list1 == null) {
return list2;
}
else if (list2 == null) {
return list1;
}
else if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
}
else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
}
}
终止条件:当两个链表都为空时,表示我们对链表已合并完成。
如何递归:我们判断 list1 和 list2 头结点哪个更小,然后较小结点的 next 指针指向其余结点的合并结果。(调用递归)
参考:
一看就会,一写就废?详解递归
【面试高频系列】一道结合「简单数据结构 & 简单算法」的面试题
三、既能考察对「数据结构」的掌握,还能考察对「递归函数」的设计
24. 两两交换链表中的节点
leetcode题目链接:24. 两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
输入:head = [1,2,3,4]
输出:[2,1,4,3]
1. 递归解法
链表和树的题目天然适合使用递归来做。
我们可以设计一个递归函数,接受一个 ListNode 节点 root 作为参数,函数的作用是将 root 后面的两个节点进行交换,交换完成后再将下一个节点传入 …
交换的前提条件:节点 root 后面至少有两个节点。
class Solution {
public ListNode swapPairs(ListNode head) {
// 递归
if(head == null || head.next == null) return head;
ListNode next = head.next;
ListNode newNode = swapPairs(next.next);
next.next = head;
head.next = newNode;
return next;
}
}
2. 迭代解法(哨兵技巧)
做有关链表的题目,有个常用技巧:添加一个虚拟头结点(哨兵),帮助简化边界情况的判断。
class Solution {
public ListNode swapPairs(ListNode head) {
// 设置虚拟头节点,交换相邻两个元素
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode tmp = dummy;
while(tmp.next != null && tmp.next.next != null) {
ListNode node1 = tmp.next;
ListNode node2 = tmp.next.next;
tmp.next = node2;
node1.next = node2.next;
node2.next = node1;
tmp = node1;
}
return dummy.next;
}
}
参考:
【面试高频系列】既能考察对「数据结构」的掌握,还能考察对「递归函数」的设计
四、一道可以考察「二分」本质的面试题
33. 搜索旋转排序数组
leetcode题目链接:33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
示例一:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例二:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
进阶:你可以设计一个时间复杂度为 O(log n) 的解决方案吗?
1. 朴素解法
但凡是从有序序列中找某个数,我们第一反应应该是「二分」。
这道题是一个原本有序的数组在某个点上进行了旋转,其实就是将原本一段升序的数组分为了两段。
我们可以先找到旋转点 idx,然后对 idx 前后进行「二分」:
class Solution {
public int search(int[] nums, int target) {
int index = 0; // 找到旋转点
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i] > nums[i + 1]) {
index = i;
break;
}
}
int res = find(nums, 0, index, target); // 二分查找target索引,先找上半段
if (res != -1) return res;
if (index + 1 < nums.length) res = find(nums, index + 1, nums.length - 1, target); // 找下半段
return res;
}
public int find(int[] nums, int l, int r, int target) {
while(l < r) {
int mid = (r - l) / 2 + l;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return nums[l] == target ? l : -1;
}
}
2. 二分解法(二次二分)
不难发现,虽然在朴素解法中我们应用了「二分」查找。
但理论复杂度为 O(n),实际复杂度也远达不到 O(log n),执行效率取决于旋转点 idx 所在数组的下标位置。
那么我们如何实现 O(log n) 的解法呢?
这道题其实是要我们明确「二分」的本质是什么。
「二分」不是单纯指从有序数组中快速找某个数,这只是「二分」的一个应用。
「二分」的本质是两段性,并非单调性。只要一段满足某个性质,另外一段不满足某个性质,就可以用「二分」。
经过旋转的数组,显然前半段满足 >= nums[0],而后半段不满足 >= nums[0]。我们可以以此作为依据,通过「二分」找到旋转点。
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) return -1;
if (n == 1) return nums[0] == target ? 0 : -1;
// 第一次「二分」:找旋转点
// 由于第一段满足 >=nums[0],第二段不满足 >=nums[0],当使用 >=nums[0] 进行二分,二分出的是满足此性质的最后一个数
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (nums[mid] >= nums[0]) {
l = mid;
} else {
r = mid - 1;
}
}
// 通过和 nums[0] 进行比较,得知 target 是在旋转点的左边还是右边
if (target >= nums[0]) {
l = 0;
} else {
l = l + 1;
r = n - 1;
}
// 第二次「二分」:找 target
while (l < r) {
int mid = l + r + 1 >> 1;
if (nums[mid] <= target) {
l = mid;
} else {
r = mid - 1;
}
}
return nums[r] == target ? r : -1;
}
}
3. 二分解法(一次二分)
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) return -1;
if (n == 1) return nums[0] == target ? 0 : -1;
int l = 0, r = n - 1;
while (l <= r) {
int mid = (r - l) / 2 + l;
if (nums[mid] == target) {
return mid;
}
if (nums[0] <= nums[mid]) {
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}
二分查找的一些细节还是不同的,可以看到,方法二和方法三的就不一样,详细可参考:算法(Java)——二分法查找。
参考:
搜索旋转排序数组
【面试高频系列】一道可以考察「二分」本质的面试题
五、翻转整数
7. 整数反转
leetcode题目链接:7. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例一:
输入:x = 123
输出:321
示例二:
输入:x = -123
输出:-321
示例三:
输入:x = 120
输出:21
1. 不完美解法
对于本题,题目从文字上限制我们只能使用 32 位的数据结构(int)。
但由于数据范围过大,使用 int 会有溢出的风险,所以我们使用 long 来进行计算,在返回再转换为 int :
class Solution {
public int reverse(int x) {
long res = 0;
while (x != 0) {
res = res * 10 + x % 10;
x = x / 10;
}
return (int)res == res ? (int)res : 0;
}
}
2. 完美解法
在「不完美解法」中,我们使用了不符合文字限制的 long 数据结构。
接下来我们看看,不使用 long 该如何求解。
从上述解法来看,我们在循环的 res = res * 10 + x % 10 这一步会有溢出的风险,因此我们需要边遍历边判断是否溢出:
- 对于正数而言:溢出意味着
res * 10 + x % 10 > Integer.MAX_VALUE,对等式进行变化后
可得res > (Integer.MAX_VALUE - x % 10) / 10)。所以我们可以根据此变形公式进行预判断 - 对于负数而言:溢出意味着
res * 10 + x % 10 < Integer.MIN_VALUE,对等式进行变化后
可得res < (Integer.MIN_VALUE - x % 10) / 10)。所以我们可以根据此变形公式进行预判断
class Solution {
public int reverse(int x) {
int res = 0;
while (x != 0) {
if (x > 0 && res > (Integer.MAX_VALUE - x % 10) / 10) return 0;
if (x < 0 && res < (Integer.MIN_VALUE - x % 10) / 10) return 0;
res = res * 10 + x % 10;
x = x / 10;
}
return res;
}
}