深度学习从入门到精通——生成对抗网络原理
生成对抗网络
-
- GANs本质上在做的事情
- 要求
- 产生问题
-
- JS Div距离偏差问题
- 训练速度问题
- JS Div距离偏差问题
- FGAN---深度理解GAN理论
-
- 观点
- 推导
- JS Div不是最佳的Div
- LSGAN
-
- 最小二乘法GAN
- WGAN
-
- 解决问题
- EM距离
- WGAN
-
-
- WGAN 的判别器的目标表达式:
-
- 限制方法
-
- 对判别器增加条件
- SNGAN
- 出现问题
- 思路
- 频谱范数
- 奇异值分解
-
- 奇异值定义
- 奇异值分解定理
- 频谱范数正则化
- SNGAN的实现
GANs本质上在做的事情
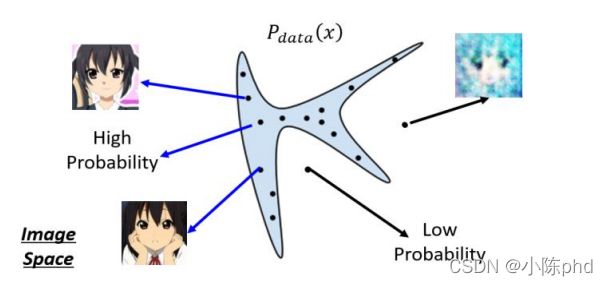
我们假设把每一个图片看作二维空间中的一个点,并且现有图片会满足于某个数据分布,我们记作()。以人脸举例,在很大的一个图像分布空间中,实际上只有很小一部分的区域是人脸图像。如上图所示,只有在蓝色区域采样出的点才会看起来像人脸,而在蓝色区域以外的区域采样出的点就不是人脸。今天我们需要做的,就是让机器去找到人脸的分布函数。具体来说,就是我们会有很多人脸图片数据,我们观测这些数据的分布,大致能猜测到哪些区域出现人脸图片数据的概率比较高,但是如果让我们找出一个具体的定义式,去给明这些人脸图片数据的分布规律,我们是没有办法做到的。但是如今,我们有了机器学习,希望机器能够学习到这样一个分布规律,并能够给出一个极致贴合的表达式。
简单来说, 就是我们有一个生成器 P G P_{G} PG 和一组参数 θ \theta θ, 我们还有从真实分布 P data ( x ) P_{\text {data }}(x) Pdata (x) 中采 样出的数据 { x 1 , x 2 , … x m } \left\{x^{1}, x^{2}, \ldots x^{m}\right\} {x1,x2,…xm}, 我们不知道数据的真实分布具体长什么样, 但是我们希望不断地调 整 P G P_{G} PG 和 θ \theta θ, 让 P G ( x ; θ ) P_{G}(x ; \theta) PG(x;θ) 越接近 P data ( x ) P_{\text {data }}(x) Pdata (x) 越好。具体的做法是, 对于每一组参数 θ \theta θ 和真实分布的 抽样 x i x^{i} xi, 我们能够计算出参数 θ \theta θ 下的生成器生成该真实抽样 x i x^{i} xi 的 likelihood, 于是我们希望找 到一个最佳的参数组 ∗ { }^{*} ∗, 使得生成器的结果最接近 P data ( x ) P_{\text {data }}(x) Pdata (x), 也就是对于每个真实抽样 x i x^{i} xi 的 likelihood 都最大, 这等价于所有真实抽样 x i x^{i} xi 的 likelihood 的乘积最大, 那原始问题就转换为 如下这个最大似然问题:
L = ∏ i = 1 m P G ( x i ; θ ) L=\prod_{i=1}^{m} P_{G}\left(x^{i} ; \theta\right) L=i=1∏mPG(xi;θ)
下面我们需要求解这个maximizing the likelihood问题,我们先证明,它其实等价于求minimize KL Divergence(KL Divergence是一个衡量两个分布之间的差异的计算式)问题。实质,最小化分布之间的差距。,模型学习的是真实数据的分布。
要求
我们需要训练出这样的 生成器, 对于一个已知分布的数据 z z z, 它可以把数据 z z z 转化成一个末知分布的数据 x x x, 这个 末知分布可以与 z z z 所在的分布完全不一样, 我们把它称作 P G ( x ) P_{G}(x) PG(x), 并且我们希望 P G ( x ) P_{G}(x) PG(x) 与 P data ( x ) P_{\text {data }}(x) Pdata (x) 之间的散度距离 (Divergence, 下称 Div) 越小越好。如果能找到这样的 P G P_{G} PG, 那也就 意味着我们找到了真实数据分布 P data ( x ) P_{\text {data }}(x) Pdata (x) 的近似解, 也就意味着我们能够生成各种各样符合 真实分布规律的数据。
产生问题
JS Div距离偏差问题
判别器:最大化̃求解 P data ( x ) P_{\text {data }}(x) Pdata (x) 与 P G ( x ) P_{G}(x) PG(x) 之间的JS Div距离。
生成器:最小化̃求解最小化与之间的JS Div距离。
-
生成器训练一次:
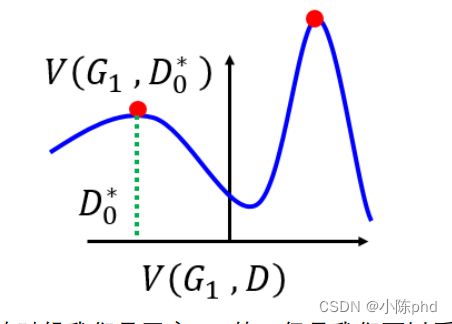
假设上面这张图是判别器训练完成之后, 找到了 D = D 0 ∗ D=D_{0}^{*} D=D0∗ 使得 V ( G 0 , D ) V\left(G_{0}, D\right) V(G0,D) 最大, 接下来我们
开始训练生成器部分。
假设训练了一次生成器之后, G 0 G_{0} G0 变成 G 1 , V ( G 0 , D ) G_{1}, V\left(G_{0}, D\right) G1,V(G0,D) 变成了下图的 ∨ ( G 1 , D ) \vee\left(G_{1}, D\right) ∨(G1,D) 。、因为在训练生成器的时候我们是固定 D \mathrm{D} D 的, 但是我们可以看到在生成器时,经过微调后的 D 0 ∗ D_{0}^{*} D0∗将 不再是让 V ( G 1 , D ) \mathrm{V}\left(G_{1}, D\right) V(G1,D) 达到最大值的解, 也就是说从这时开始, 把 D = D 0 ∗ \mathrm{D}=D_{0}^{*} D=D0∗ 代入 V ( G , D ) \mathrm{V}(\mathrm{G}, D) V(G,D) 中计算出的值不再等 于 P data P_{\text {data }} Pdata 与 P G P_{G} PG 之间的 JS Div 距离(只有Max V ( G , D ) (\mathrm{G}, D) (G,D) 才等于 JS 距离), 那么在接下来在继续训 练生成器的过程中, minimize 的值就不再会是 P data P_{\text {data }} Pdata 与 P G P_{G} PG 之间的 JS Div 距离了。
训练速度问题
GAN中,判别器对于仿造数据的处理式是:
E x ∼ P G [ log ( 1 − D ( x ) ) ] E_{x \sim P_{G}}[\log (1-D(x))] Ex∼PG[log(1−D(x))]
我们注意到, log ( 1 − D ( x ) ) \log (1-D(x)) log(1−D(x)) 这个表达式, − - − 开始减得很慢, 后面减得很快, 我们不妨与 − log ( D ( x ) ) -\log (\mathrm{D}(\mathrm{x})) −log(D(x)) 这个表达式对比一下: 一开始判别器是很容易鉴别仿造数据的, 因此 D(x)的初始值是在靠近 0 的左端。而对于刚开始训练的模型, 我们希望在初期 D x \mathrm{x} x )能够快速地更新, 但不幸的是, 目标函数 log ( 1 − D ( x ) ) \log (1-\mathrm{D}(\mathrm{x})) log(1−D(x)) 左端刚好是平缓的区域, 依据梯度下降原理这会阻碍 D(x)的快速更新。为了解决这一问题, 有人提出了把 log ( 1 − D ( x ) ) \log (1-\mathrm{D}(\mathrm{x})) log(1−D(x)) 这个表达式换成 − log ( D ( x ) ) -\log (\mathrm{D}(\mathrm{x})) −log(D(x)), 同样能满足判别器的目标函数要求, 并且在训练初期还能更新得比较快。上述方法便是在这个非常小的地方做了改进。不过后来, 人们为了区分这两种 GAN,还是分别起了不同的名字。第一种 GAN 被叫做 MMGAN (Minimax GAN), 它也是人们常说的原始 GANs; 第二种 GAN 被叫做 NSGAN (Non-saturating GAN)。
JS Div距离偏差问题
可以通过限制训练次数来解决。对于判别器, 理论上我们需要让它训练非常多 次, 直到判别器找到的 D 0 ∗ D_{0}^{*} D0∗ 是 ArgMax V ( G , D ) \operatorname{ArgMax} V(\mathrm{G}, D) ArgMaxV(G,D) 的全局最大解, 这样 D 0 ∗ D_{0}^{*} D0∗ 在传给生成器时才能保证 V ( G , D ) \mathrm{V}(\mathrm{G}, D) V(G,D) 是 P data P_{\text {data }} Pdata 与 P G P_{G} PG 之间的 JS Div 距离; 而对于生成器, 我们限制它只能训练 1 次, 这是为 了防止训练完一次后 V ( G , D ) \mathrm{V}(\mathrm{G}, D) V(G,D) 发生变化导致 D 0 ∗ D_{0}^{*} D0∗ 不再是 ArgMaxV ( G , D ) \operatorname{ArgMaxV}(\mathrm{G}, D) ArgMaxV(G,D) 的解。于是原始的算法优 化为如下算法:
不过, 在实际操作中我们往往不会非常多次地训练判别器, 因为找到真正的解 D 0 ∗ 需要的 D_{0}^{* \text { 需要的 }} D0∗ 需要的 训练次数太多, 为了减小训练代价我们只会训练 k \mathrm{k} k 次, 找到 D 0 ∗ D_{0}^{*} D0∗ 的近似解 D 0 ∼ D_{0}^{\sim} D0∼ 即可停止。所以 在实际的应用中, 我们计算的都是 JS Div 的近似值, 最终 GANS 学到的是近似分布而不是数 据的真实分布, 这是我们需要明白的地方。
FGAN—深度理解GAN理论
观点
任何的Div(统称为f-Div)都可以被放到GANs的架构中去。
推导
设定P和Q是两个不同的分布, p(x)和 q(x)代表着分别从P和Q 采样出x的几率,则我们将f-Div 定义为:
D f ( P ∥ Q ) = ∫ x q ( x ) f ( p ( x ) q ( x ) ) Θ d x D_{f}(P \| Q)=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right)_{\Theta} d x Df(P∥Q)=∫xq(x)f(q(x)p(x))Θdx
上述公式衡量P和Q有多不一样,公式里边的函数f可以是很多不同的版本,只要 f满足以下条件:它是一个凸函数同时 f(1)=0 。 稍微分析一下这个公式:
-
假设对于所有的 x来说,都有 p(x)=q(x),则有D�(P,Q)=0,也就是意味着两个分布没有区别,和假设一样。
-
同时 0 是 D f D_f Df能取到的最小值:
-
D f ( p ∥ q ) = ∫ x q ( x ) f ( p ( x ) q ( x ) ) d x ≥ f ( ∫ q ( x ) p ( x ) q ( x ) d x ) = f ( 1 ) = 0 D_{f}(p \| q)=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) d x \geq f\left(\int q(x) \frac{p(x)}{q(x)} d x\right)=f(1)=0 Df(p∥q)=∫xq(x)f(q(x)p(x))dx≥f(∫q(x)q(x)p(x)dx)=f(1)=0
也就是说, 只要两个分布稍有不同, 就能通过 D f \mathrm{D}_{f} Df 得到的正值反映出来。这个时候我们 发现之前常用的 KL Div 其实就是 F Div 的一种。
当你设置 f(x)=xlogx,即将 F Div 转换为了 KL Div 了。
D f ( P ∥ Q ) = ∫ x q ( x ) p ( x ) q ( x ) log ( p ( x ) q ( x ) ) d x = ∫ x p ( x ) log ( p ( x ) q ( x ) ) d x D_{f}(P \| Q)=\int_{x} q(x) \frac{p(x)}{q(x)} \log \left(\frac{p(x)}{q(x)}\right) d x=\int_{x} p(x) \log \left(\frac{p(x)}{q(x)}\right) d x Df(P∥Q)=∫xq(x)q(x)p(x)log(q(x)p(x))dx=∫xp(x)log(q(x)p(x))dx当你设置 f ( x ) = x log x \mathrm{f}(\mathrm{x})=\mathrm{x} \log \mathrm{x} f(x)=xlogx, 即将 F \mathrm{F} F Div 转换为了 K L \mathrm{KL} KL Div 了。
D f ( P ∥ Q ) = ∫ x q ( x ) ( − log ( p ( x ) q ( x ) ) ) d x = ∫ x q ( x ) log ( q ( x ) p ( x ) ) d x D_{f}(P \| Q)=\int_{x} q(x)\left(-\log \left(\frac{p(x)}{q(x)}\right)\right) d x=\int_{x} q(x) \log \left(\frac{q(x)}{p(x)}\right) d x Df(P∥Q)=∫xq(x)(−log(q(x)p(x)))dx=∫xq(x)log(p(x)q(x))dx
不只是JS Div,任何的Div(统称为f-Div)都可以被放到GANs的架构中去。
JS Div不是最佳的Div
-
大多数情况下 P G P_{G} PG 与 P data P_{\text {data }} Pdata 是没有重合的。
-
因为一方面, 从理论上来说, P G P_{G} PG 与 P data P_{\text {data }} Pdata 都属于高维空间中的低维流形, 者具有重合的可能性是非常低的;
-
从实际上来看, 即算 P G P_{G} PG 与 P d a t a P_{d a t a} Pdata 的分布有 了重合区域 (如下左图), 但是在实际训练中我们是从 P G P_{G} PG 与 P data P_{\text {data }} Pdata 中取的采样, 这些采样形 成的分布很有可能是互不相交的(如下右图), 我们仍然能找到一条分割线将 P G P_{G} PG 与 P data 完美 P_{\text {data 完美 }} Pdata 完美 分割开来(如右图中的黑线)。所以我们可以认为, 大多数情况下 P G P_{G} PG 与 P data P_{\text {data }} Pdata 是没有重合 的
-
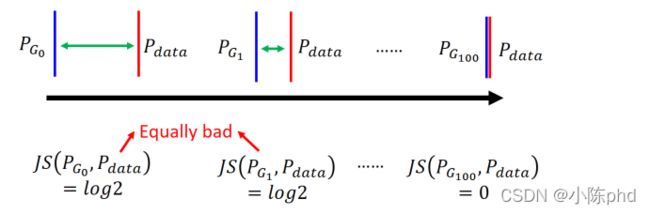
那如果 P G P_{G} PG 与 P data P_{\text {data }} Pdata 是没有重合的,然后用 JS Div 去衡量 P G P_{G} PG 与 P data P_{\text {data }} Pdata 的距离的话, 就会造成 如下障碍:
在上图中可以看出,0与1都与没有交集,但是1与的距离比0与的距离近,然而用 JS Div 去衡量二者的距离却是一样的,都为 log2,这是我们认为 JS Div 不合理的地方,因为实际情况是Div(1 ,)应当比Div(0 ,)要小,才能反映出1 与比0 与要靠的更近。有必要说明一下,为什么如果两个分布完全没有重合的话,那么这两个分布的 JS Div 会是一样的。前面有提到,JS Div 是通过判别器计算出来的,而判别器的本质是二分类器,只要与完全没有重合,判别器就能 100%地鉴别出()与()的差异,因此二者的 JS Div 就是一样的。
LSGAN
最小二乘法GAN
-
出现的问题是什么?
只要与完全没有重合,判别器就能 100%地鉴别出()与()的差异,因此二者的 JS Div 就是一样的。
-
解决思路
- 让判别器始终都不能 100%地鉴别出()与()的差异,这样即便与完全没有重合,二者的 JS Div 也会不一样,而只要 Div 存在差异,就能反映出的优劣度来。
这是判别器训练得太好的例子,色样本点,是生成样本,它们的得分为 0;绿色样本点,是真实样本,它们的得分为 1;当轮到生成器训练的时候,它希望蓝色的点能够向右移,但是因为对于所有蓝色点,判别器计算出的 JS Div 都是一样的,这意味着所有点的梯度都是 0,生成器无法更新。
-
如何限制判别器训练
换个差的判别模型,聪明的训练的太好,那就直接弄个差的。例:判别器的最后的 sigmoid 激活层改成 linear 激活层
-
遗留个问题:如何去更好地测量与之间的 Div
WGAN
解决问题
如何去更好地测量与之间的 Div
WGAN 的全称是 WassersteinGAN,它提出了用 Wasserstein 距离(也称 EM 距离)去取代JS 距离,这样能更好的衡量两个分布之间的 Div。我们先介绍一下什么是 EM 距离。
EM距离
EM 距离的全称是 EarthMover(推土距离),它的定义非常直观:假设有两堆数据分布 P和 Q,看作两堆土,现在把 P 这堆土推成 Q 这堆土所需要的最少的距离就是 EM 距离。
假设 P 的分布是上图棕色柱块区域,Q 的分布是上图绿色柱块区域,现在需要把 P 的分布推成 Q 的分布,我们可以制定出很多不同的 MovingPlan(推土计划)。
这些不同的推土计划都能把分布 P 变成分布 Q,但是它们所要走的平均推土距离是不一样的,我们最终选取最小的平均推土距离值作为 EM 距离。例如上面这个例子的 EM 距离就是下面这个推土方案对应的值。
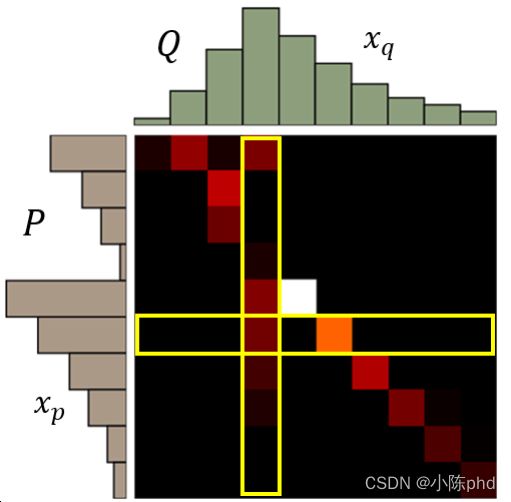
那为了更好地表示这个推土问题,我们可以把每一个 moving plan 转化为一个矩阵图:
每一个色块表示 P 分布到 Q 分布需要分配的土量(移动距离),那每一行的色块之和就是 P 分布该行位置的柱高度,每一列的色块之和就是 Q 分布该列位置的柱高度。于是我们的求解目标表达式就如下所示:
表达式中γ函数计算当前计划下到的推土量,||-||表示二者间的推土距离。 那如果这个时候我们想直接求解这个表达式的话,是非常麻烦的,因为需要穷举所有的moving plan 然后再选择其最小值。如果我们对之前的理论有印象的话,我们会想到这个优化问题依然可以交给判别器来解决。 于是接下来要做的,就是去改判别器,让它能够衡量与之间的 wasserstein 距离。
WGAN
WGAN 的判别器的目标表达式:
V ( G , D ) = max D ∈ 1 − Lipschitz { E x ∼ P data [ D ( x ) ] − E x ∼ P G [ D ( x ) ] } V(G, D)=\max _{D \in 1-\text { Lipschitz }}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_{G}}[D(x)]\right\} V(G,D)=D∈1− Lipschitz max{Ex∼Pdata [D(x)]−Ex∼PG[D(x)]}
这个表达式的求解结果就是 P G P_{G} PG 与 P data P_{\text {data }} Pdata 之间的 wasserstein 距离。反正目前我们构造出了求解 was 距离的判别器。关于这个表达式,值得注意的是, D D D 被加上了 1-Lipschitz function(如下图)的限制。
∥ f ( x 1 ) − f ( x 2 ) ∥ ≤ K ∥ x 1 − x 2 ∥ K = 1 for "1 − Lipschitz" \begin{aligned} &\left\|f\left(x_{1}\right)-f\left(x_{2}\right)\right\| \leq K\left\|x_{1}-x_{2}\right\| \\ &\mathrm{K}=1 \text { for "1 }-\text { Lipschitz" } \end{aligned} ∥f(x1)−f(x2)∥≤K∥x1−x2∥K=1 for "1 − Lipschitz"
需要要对判别器做限制。传统 GANs 的判别器输出的结果是在**(0,1)区间之内,但是在 WGAN 中输出的结果是 was 距离,was 距离是没有上下界的**,这意味着,随着训练进行,的 was 值会越来越小,的 was 值会越来越大,判别器将永远无法收敛。
限制方法
- weight clipping
- 设定一个上限 c 与下限-c,如果更新参数 w 大于 c,改成 w=c;如果更新参数 w 小于-c,改成 w=-c。
- 无法让D限制在 1-Lipschitz function
- WGAN-GP以及SNGAN
D ∈ 1 - Lipschitz ⇔ ∥ ∇ x D ( x ) ∥ ≤ 1 for all x D \in 1 \text { - Lipschitz } \Leftrightarrow\left\|\nabla_{x} D(x)\right\| \leq 1 \text { for all } \mathrm{x} D∈1 - Lipschitz ⇔∥∇xD(x)∥≤1 for all x
对于一个可微函数,当且仅当对于任意的 x,梯度的模都小于或等于 1,则该可微函数是 1-Lipschitz function。
对判别器增加条件
V ( G , D ) ≈ max D { E x ∼ P data [ D ( x ) ] − E x ∼ P G [ D ( x ) ] − λ ∫ x max ( 0 , ∥ ∇ x D ( x ) ∥ − 1 ) d x } \begin{aligned} V(G, D) \approx & \max _{D}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_{G}}[D(x)]\right.\\ &\left.-\lambda \int_{x} \max \left(0,\left\|\nabla_{x} D(x)\right\|-1\right) d x\right\} \end{aligned} V(G,D)≈Dmax{Ex∼Pdata [D(x)]−Ex∼PG[D(x)]−λ∫xmax(0,∥∇xD(x)∥−1)dx}
-
出现的问题:统计的就是所有梯度的模不满足小于或等于 1 的项,给这些项分配一个惩罚参数λ,计算出惩罚值,并将所有惩罚值累加起来。当这个累加惩罚够大时,它会拖累maxD{V(D, G)}的取值,最终导致这样的 D 不再是最优解。惩罚力度过大导致最优解出现偏差。
-
真正需要考虑的惩罚项,应该是对判别器产生实质影响的区域。考虑到整个WGAN 的目的是让渐渐向靠拢,那位于和之间的区域一定会对判别器产生实质的影响。因此,我们将惩罚项中 x 的范围缩小为,是介于和之间的区域。目标表达式转化为如下式子:
V ( G , D ) ≈ max D { E x ∼ P data [ D ( x ) ] − E x ∼ P G [ D ( x ) ] − λ E x ∼ P penalty [ max ( 0 , ∥ ∇ x D ( x ) ∥ − 1 ) ] } \begin{aligned} V(G, D) \approx & \max _{D}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_{G}}[D(x)]\right.\\ &\left.-\lambda E_{x \sim P_{\text {penalty }}}\left[\max \left(0,\left\|\nabla_{x} D(x)\right\|-1\right)\right]\right\} \end{aligned} V(G,D)≈Dmax{Ex∼Pdata [D(x)]−Ex∼PG[D(x)]−λEx∼Ppenalty [max(0,∥∇xD(x)∥−1)]}
∥ ∇ x D ( x ) ∥ \left\|\nabla_{x} D(x)\right\| ∥∇xD(x)∥训练得越快,效果也越好,于是不妨把表达式直接改成:
V ( G , D ) ≈ max D { E x ∼ P data [ D ( x ) ] − E x ∼ P G [ D ( x ) ] − λ E x ∼ P penalty [ ( ∥ ∇ x D ( x ) ∥ − 1 ) 2 ] } \begin{aligned} V(G, D) \approx & \max _{D}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_{G}}[D(x)]\right.\\ &\left.-\lambda E_{x \sim P_{\text {penalty }}}\left[\left(\left\|\nabla_{x} D(x)\right\|-1\right)^{2}\right]\right\} \end{aligned} V(G,D)≈Dmax{Ex∼Pdata [D(x)]−Ex∼PG[D(x)]−λEx∼Ppenalty [(∥∇xD(x)∥−1)2]}
在惩罚项中希望 ∥ ∇ x D ( x ) ∥ \left\|\nabla_{x} D(x)\right\| ∥∇xD(x)∥越接近 1,惩罚就越少。平滑惩罚因子。
WGAN-GP:只是对于梯度的模大于 1 的区域的 x 作出了惩罚,它并没有保证每一个 x 的梯度的模都小于或等于 1
SNGAN
出现问题
需要保证对于每一个位置的 x,梯度的模都小于等于 1。
思路
SNGAN(频谱归一化 GAN)为了让正则化产生更明确地限制,提出了用谱范数标准化神经网络的参数矩阵 W,从而让神经网络的梯度被限制在一个范围内。
频谱范数
对于小扰动 ξ,我们有
∥ f Θ ( x + ξ ) − f ( x ) ∥ 2 ∥ ξ ∥ 2 = ∥ ( W Θ , x ( x + ξ ) + b Θ , x ) − ( W Θ , x x + b Θ , x ) ∥ 2 ∥ ξ ∥ 2 = ∥ W Θ , x ξ ∥ 2 ∥ ξ ∥ 2 ≤ σ ( W Θ , x ) \frac{\left\|f_{\Theta}(\boldsymbol{x}+\boldsymbol{\xi})-f(\boldsymbol{x})\right\|_{2}}{\|\boldsymbol{\xi}\|_{2}}=\frac{\left\|\left(W_{\Theta, \boldsymbol{x}}(\boldsymbol{x}+\boldsymbol{\xi})+\boldsymbol{b}_{\Theta, \boldsymbol{x}}\right)-\left(W_{\Theta, \boldsymbol{x}} \boldsymbol{x}+\boldsymbol{b}_{\Theta, \boldsymbol{x}}\right)\right\|_{2}}{\|\boldsymbol{\xi}\|_{2}}=\frac{\left\|W_{\Theta, \boldsymbol{x}} \boldsymbol{\xi}\right\|_{2}}{\|\boldsymbol{\xi}\|_{2}} \leq \sigma\left(W_{\Theta, \boldsymbol{x}}\right) ∥ξ∥2∥fΘ(x+ξ)−f(x)∥2=∥ξ∥2∥(WΘ,x(x+ξ)+bΘ,x)−(WΘ,xx+bΘ,x)∥2=∥ξ∥2∥WΘ,xξ∥2≤σ(WΘ,x)
其中 σ ( W θ , x ) 就是 W θ , x 的谱范数的计算式, 数学上它等价于计算矩阵 W θ , x 的最大奇异值 \text { 其中 } \sigma\left(W_{\theta, x}\right) \text { 就是 } W_{\theta, x} \text { 的谱范数的计算式, 数学上它等价于计算矩阵 } W_{\theta, x} \text { 的最大奇异值 } 其中 σ(Wθ,x) 就是 Wθ,x 的谱范数的计算式, 数学上它等价于计算矩阵 Wθ,x 的最大奇异值
矩阵最大奇异值的表达式参见下式:
σ ( A ) = max ξ ∈ R n , ξ ≠ 0 ∥ A ξ ∥ 2 ∥ ξ ∥ 2 \sigma(A)=\max _{\boldsymbol{\xi} \in \mathbb{R}^{n}, \boldsymbol{\xi} \neq \mathbf{0}} \frac{\|A \boldsymbol{\xi}\|_{2}}{\|\boldsymbol{\xi}\|_{2}} σ(A)=ξ∈Rn,ξ=0max∥ξ∥2∥Aξ∥2
- 应当训练模型参数Θ,使得对于任何 x,Θ,x的谱范数都很小,进一步研究 W Θ , x W_{\Theta, \mathrm{x}} WΘ,x 的性质, 让我们假设每个激活函数 f l f^{l} fl 都是 ReLU(该参数可以很容易地推广 到其他分段线性函数)。注意, 对于给定的向量 x , f l \mathrm{x}, f^{l} x,fl 充当对角矩阵 D Θ , x ′ l D_{\Theta, \mathrm{x}^{\prime}}^{l} DΘ,x′l, 其中如果 x l − 1 x^{l-1} xl−1 中的 对应元素为正, 则对角线中的元素等于 1; 否则, 它等于零(这是 ReLU 的定义)于是, 我 们可以重写 W Θ , x W_{\Theta, x} WΘ,x 为下式:
W Θ , x = D Θ , x L W L D Θ , x L − 1 W L − 1 ⋯ D Θ , x 1 W 1 W_{\Theta, x}=D_{\Theta, x}^{L} W^{L} D_{\Theta, x}^{L-1} W^{L-1} \cdots D_{\Theta, x}^{1} W^{1} WΘ,x=DΘ,xLWLDΘ,xL−1WL−1⋯DΘ,x1W1
又注意到对于每个 l ∈ { 1 , … , L } l \in\{1, \ldots, L\} l∈{1,…,L}, 有 σ ( D θ , x l ) ⩽ 1 \sigma\left(D_{\theta, \mathrm{x}}^{l}\right) \leqslant 1 σ(Dθ,xl)⩽1, 所以我们有:
σ ( W Θ , x ) ≤ σ ( D Θ , x L ) σ ( W L ) σ ( D Θ , x L − 1 ) σ ( W L − 1 ) ⋯ σ ( D Θ , x 1 ) σ ( W 1 ) ≤ ∏ ℓ = 1 L σ ( W ℓ ) \sigma\left(W_{\Theta, x}\right) \leq \sigma\left(D_{\Theta, x}^{L}\right) \sigma\left(W^{L}\right) \sigma\left(D_{\Theta, x}^{L-1}\right) \sigma\left(W^{L-1}\right) \cdots \sigma\left(D_{\Theta, x}^{1}\right) \sigma\left(W^{1}\right) \leq \prod_{\ell=1}^{L} \sigma\left(W^{\ell}\right) σ(WΘ,x)≤σ(DΘ,xL)σ(WL)σ(DΘ,xL−1)σ(WL−1)⋯σ(DΘ,x1)σ(W1)≤ℓ=1∏Lσ(Wℓ)
为了限制Θ,x的谱范数,只需要每个 ∈ {1, … , }, 限制的谱范数就足够了。这促使我们考虑谱范数正则化
奇异值分解
奇异值定义
设 A A A 为 m ⋆ n m \star n m⋆n 矩阵, q = min ( m , n ) , A ⋆ A q=\min (m, n), A \star A q=min(m,n),A⋆A 的 q q q 个非负特征值的算术平方根叫作 A A A 的奇异值。
奇异值分解定理
设给定 A ∈ M n , m A \in M_{n, m} A∈Mn,m, 令 q = min { m , n } q=\min \{m, n\} q=min{m,n}, 并假设 rankA = r \operatorname{rankA}=r rankA=r :
(a) 存在酉矩阵 V ∈ M n V \in M_{n} V∈Mn 与 W ∈ M m W \in M_{m} W∈Mm, 以及一个对角方阵
∑ q = [ σ 1 … 0 … … … 0 … σ q ] \sum_{q}=\left[\begin{array}{ccc} \sigma_{1} & \ldots & 0 \\ \ldots & \ldots & \ldots \\ 0 & \ldots & \sigma_{q} \end{array}\right] q∑=⎣⎡σ1…0………0…σq⎦⎤
使得 σ 1 ≥ σ 2 ≥ … ≥ σ r > 0 = σ r + 1 = … = σ q \sigma_{1} \geq \sigma_{2} \geq \ldots \geq \sigma_{r}>0=\sigma_{r+1}=\ldots=\sigma_{q} σ1≥σ2≥…≥σr>0=σr+1=…=σq 以及 A = V ∑ W ∗ A=V \sum W^{*} A=V∑W∗,
其中 ∑ = { ∑ q if m = n [ ∑ q 0 ] ∈ M n , m if m > n [ ∑ q 0 ] T ∈ M n , m if m < n \text { 其中 } \sum=\left\{\begin{array}{cc} \sum_{q} & \text { if } m=n \\ {\left[\sum_{q}\right.} & 0] \in M_{n, m} & \text { if } m>n \\ {\left[\sum_{q}\right.} & 0]^{T} \in M_{n, m} & \text { if } m
(b) 参数 σ 1 , σ 2 , … , σ r \sigma_{1}, \sigma_{2}, \ldots, \sigma_{r} σ1,σ2,…,σr 是 A A ∗ A A^{*} AA∗ 的按照递减次序排列的非零特征值的正的平方根, 它 们与 A A ∗ A A^{*} AA∗ 的按照递减次序排列的非零特征值的正的平方根是相同的。
在奇异值分解定理中, 矩阵 ∑ \sum ∑ 的对角元素(即纯量 σ 1 , σ 2 , … , σ q \sigma_{1}, \sigma_{2}, \ldots, \sigma_{q} σ1,σ2,…,σq, 它们是方阵 ∑ \sum ∑ q的对 角元素) 称为矩阵 A A A 的奇异值。
频谱范数正则化
为了约束每个权重矩阵的频谱范数 W l W^{l} Wl, 我们考虑以下经验风险最小化问题:
minimize Θ 1 K ∑ i = 1 K L ( f Θ ( x i ) , y i ) + λ 2 ∑ ℓ = 1 L σ ( W ℓ ) 2 \underset{\Theta}{\operatorname{minimize}} \frac{1}{K} \sum_{i=1}^{K} L\left(f_{\Theta}\left(\boldsymbol{x}_{i}\right), \boldsymbol{y}_{i}\right)+\frac{\lambda}{2} \sum_{\ell=1}^{L} \sigma\left(W^{\ell}\right)^{2} ΘminimizeK1i=1∑KL(fΘ(xi),yi)+2λℓ=1∑Lσ(Wℓ)2
其中λ∈+是正则化因子,第二项被称为谱范数正则项,它降低了权重矩阵的谱准则。
在执行标准梯度下降时,我们需要计算谱范数正则项的梯度。为此,让我们考虑对于一个特定 l l l 的梯度 σ ( W l ) 2 2 / 2 \sigma\left(W^{l}\right)_{2}^{2} / 2 σ(Wl)22/2, 其中 l ∈ { 1 , … , L } l \in\{1, \ldots, L\} l∈{1,…,L} 。设 σ 1 = σ ( W l ) \sigma_{1}=\sigma\left(W^{l}\right) σ1=σ(Wl) 和 σ 2 \sigma_{2} σ2 分别是第一和第二奇异值。如 果 σ 1 > σ 2 \sigma_{1}>\sigma_{2} σ1>σ2, 则 σ ( W l ) 2 / 2 \sigma\left(W^{l}\right)^{2} / 2 σ(Wl)2/2 的梯度为 σ 1 u 1 v 1 T \sigma_{1} \mathrm{u}_{1} \mathrm{v}_{1}^{T} σ1u1v1T, 其中, u 1 \mathrm{u}_{1} u1 和 v 1 \mathrm{v}_{1} v1 分别是第一个左奇异向量和第一个右 奇异向量。如果 σ 1 = σ 2 \sigma_{1}=\sigma_{2} σ1=σ2, 则 σ ( W l ) 2 2 / 2 \sigma\left(W^{l}\right)_{2}^{2} / 2 σ(Wl)22/2 是不可微的。然而, 出于实际目的, 我们可以假设这 种情况从末发生, 因为实际训练中的数值误差会让 σ 1 \sigma_{1} σ1 和 σ 2 \sigma_{2} σ2 不可能完全相等。
由于计算 σ 1 , u 1 \sigma_{1}, u_{1} σ1,u1 和 v 1 v_{1} v1 在计算上是昂贵的, 我们使用功率迭代方法来近似它们。从随机初 始化的 ∨ \vee ∨ 开始(开始于 l − 1 l-1 l−1 层), 我们迭代地执行以下过程足够次数:
KaTeX parse error: Can't use function '$' in math mode at position 51: … \boldsymbol{v}$̲ and $\boldsymb…
最终我们得到了使用频谱范数正则项的 SGD 算法如下:
为了最大化 σ 1 , u 1 \sigma_{1}, u_{1} σ1,u1 和 v 1 v_{1} v1, 在 SGD 的下一次迭代开始时, 我们可以用 v 1 v_{1} v1 代 替第 2 步中的初始向量 v ∘ v_{\circ} v∘ 然后在第 7 步中右方的标注是,只进 行一次迭代就能够获得足够好的近似值。文章中还提到对于含有卷积的神经网络架构, 我们 需要将参数对齐为 b × a k w k h b \times a k_{w} k_{\mathrm{h}} b×akwkh 的矩阵, 再去计算该矩阵的谱范数并添加到正则项中。
综上, 频谱范数正则化看起来非常复杂, 但是它的实际做法, 可以简单地理解为, 把传 统 GANs 中的 loss 函数:
minimize Θ 1 K ∑ i = 1 K L ( f Θ ( x i ) , y i ) + λ ∑ ( w i ) 2 \underset{\Theta}{\operatorname{minimize}} \frac{1}{K} \sum_{i=1}^{K} L\left(f_{\Theta}\left(\boldsymbol{x}_{i}\right), \boldsymbol{y}_{i}\right)+\lambda \sum\left(w_{i}\right)^{2} ΘminimizeK1i=1∑KL(fΘ(xi),yi)+λ∑(wi)2
其中的正则项替换成了谱范数:
minimize Θ 1 K ∑ i = 1 K L ( f Θ ( x i ) , y i ) + λ 2 ∑ ℓ = 1 L σ ( W ℓ ) 2 \underset{\Theta}{\operatorname{minimize}} \frac{1}{K} \sum_{i=1}^{K} L\left(f_{\Theta}\left(\boldsymbol{x}_{i}\right), \boldsymbol{y}_{i}\right)+\frac{\lambda}{2} \sum_{\ell=1}^{L} \sigma\left(W^{\ell}\right)^{2} ΘminimizeK1i=1∑KL(fΘ(xi),yi)+2λℓ=1∑Lσ(Wℓ)2
并且谱范数的计算利用了功率迭代的方法去近似。
SNGAN的实现
之前我们说到,对于 GANs 最重要的目的是实现 D 的 1-lipschitz 限制,频谱范数正则化固然有效,但是它不能保证把Θ的梯度限制在一个确定的范围内,真正解决了这一问题的,是直到 18 年 2 月才被提出的 SNGAN。SNGAN 基于 spectral normalization 的思想,通过对W 矩阵归一化的方式,真正将Θ的梯度控制在了小于或等于 1 的范围内。
我们先来证明, 只要将每一层 W l W^{l} Wl 的谱范数都限制为 1 , 最终得到的 f Θ f_{\Theta} fΘ 函数就会满足 1lipschitz 限制。
对于一个线性层函数 g ( h ) = W h g(h)=W h g(h)=Wh, 我们可以计算出它的 lipschitz 范式:
∥ g ∥ L i p = sup h σ ( ∇ g ( h ) ) = sup h σ ( W ) = σ ( W ) . \|g\|_{\mathrm{Lip}}=\sup _{\boldsymbol{h}} \sigma(\nabla g(\boldsymbol{h}))=\sup _{\boldsymbol{h}} \sigma(W)=\sigma(W) . ∥g∥Lip=hsupσ(∇g(h))=hsupσ(W)=σ(W).
如果激活层函数的 lipschitz 范式 ∥ a l ∥ l i p = 1 \left\|a_{l}\right\|_{l i p}=1 ∥al∥lip=1 (比如 ReLU), 我们就有如下不等式:
∥ g 1 ∘ g 2 ∥ L i p ≤ ∥ g 1 ∥ L i p ⋅ ∥ g 2 ∥ L i p \left\|g_{1} \circ g_{2}\right\|_{\mathrm{Lip}} \leq\left\|g_{1}\right\|_{\mathrm{Lip}} \cdot\left\|g_{2}\right\|_{\mathrm{Lip}} ∥g1∘g2∥Lip≤∥g1∥Lip⋅∥g2∥Lip
其中 ∘ \circ ∘ 表示复合函数。我们利用上面的不等式, 就能够得到 f Θ f_{\Theta} fΘ 的 lipschitz 范式的限制式:
∥ f ∥ Lip ≤ ∥ ( h L ↦ W L + 1 h L ) ∥ Lip ⋅ ∥ a L ∥ Lip ⋅ ∥ ( h L − 1 ↦ W L h L − 1 ) ∥ Lip ⋯ ∥ a 1 ∥ Lip ⋅ ∥ ( h 0 ↦ W 1 h 0 ) ∥ Lip = ∏ l = 1 L + 1 ∥ ( h l − 1 ↦ W l h l − 1 ) ∥ Lip = ∏ l = 1 L + 1 σ ( W l ) \begin{aligned} \|f\|_{\text {Lip }} \leq &\left\|\left(\boldsymbol{h}_{L} \mapsto W^{L+1} \boldsymbol{h}_{L}\right)\right\|_{\text {Lip }} \cdot\left\|a_{L}\right\|_{\text {Lip }} \cdot\left\|\left(\boldsymbol{h}_{L-1} \mapsto W^{L} \boldsymbol{h}_{L-1}\right)\right\|_{\text {Lip }} \\ & \cdots\left\|a_{1}\right\|_{\text {Lip }} \cdot\left\|\left(\boldsymbol{h}_{0} \mapsto W^{1} \boldsymbol{h}_{0}\right)\right\|_{\text {Lip }}=\prod_{l=1}^{L+1}\left\|\left(\boldsymbol{h}_{l-1} \mapsto W^{l} \boldsymbol{h}_{l-1}\right)\right\|_{\text {Lip }}=\prod_{l=1}^{L+1} \sigma\left(W^{l}\right) \end{aligned} ∥f∥Lip ≤∥∥(hL↦WL+1hL)∥∥Lip ⋅∥aL∥Lip ⋅∥∥(hL−1↦WLhL−1)∥∥Lip ⋯∥a1∥Lip ⋅∥∥(h0↦W1h0)∥∥Lip =l=1∏L+1∥∥(hl−1↦Wlhl−1)∥∥Lip =l=1∏L+1σ(Wl)
于是现在, 我们只需要保证 σ ( W l ) \sigma\left(W^{l}\right) σ(Wl) 恒等于 1 , 就能够让 f Θ f_{\Theta} fΘ 函数满足 1-lipschitz 限制。做 法非常简单, 只需要将 W W W 矩阵归一化即可:
W ˉ S N ( W ) : = W / σ ( W ) \bar{W}_{\mathrm{SN}}(W):=W / \sigma(W) WˉSN(W):=W/σ(W)
可以看出,与传统的 SGD 相比,带有谱归一化的 SGD 做的额外处理就是对 W 矩阵做的归一化处理:
W ˉ S N l ( W l ) = W l / σ ( W l ) , where σ ( W l ) = u ~ l T W l v ~ l \bar{W}_{\mathrm{SN}}^{l}\left(W^{l}\right)=W^{l} / \sigma\left(W^{l}\right), \text { where } \sigma\left(W^{l}\right)=\tilde{\boldsymbol{u}}_{l}^{\mathrm{T}} W^{l} \tilde{\boldsymbol{v}}_{l} WˉSNl(Wl)=Wl/σ(Wl), where σ(Wl)=u~lTWlv~l
参考: glab.