(三)位运算
专栏:算法
上一篇:(二)基础运算
下一篇:(四)质数(素数)
目录
- 1. 常见的位运算
-
- 1.0 位运算与逻辑运算之间的关系
- 1.1 按位与
- 1.2 按位或
- 1.3 按位取反
- 1.4 按位异或
- 1.5 移位
-
- 1.5.1 左移
- 1.5.2 有符号右移(算术右移)
- 1.5.3 无符号右移(逻辑右移)
- 2. 编程语言相关
-
- 2.1 位运算操作符
- 2.2 C运算符优先级
- 2.3 整数类型之间的转换
-
- 2.3.1 低级类型向高级类型转换
- 2.3.2 高级类型向低级类型转换
- 2.3.3 整型提升
-
- 2.3.3.1 整型提升后的不同
- 3. 常用的位运算操作
-
- 3.1 二进制位 bit(n)
- 3.2 数二进制形式输出
-
- 3.2.1 itoa() 函数
- 3.2.2 手动实现二进制格式的输出
- 3.3 对应位置位
- 3.4 对应位清零
- 3.5 对应位取反
- 3.6 取二进制位
-
- 3.6.1 取二进制位
- 3.6.2 取两个二进制数不同的位
- 3.6.2 取a为1,b为0的位
- 3.7 位逆序
-
- 3.7.1 常规位逆序方法
- 3.7.2 蝴蝶算法
-
- 3.7.2.1 8位二进制数逆序
- 3.7.2.2 N N N 位二进制数逆序
- 3.8 位循环移动
- 3.9 lowbit运算
-
- 3.9.1 lowbit概念
- 3.9.2 lowbit运算的实现
- 3.9.3 消去lowbit
- 3.10 highbit运算
-
- 3.10.1 位的扩散
- 3.10.2 利用异或取最高位
- 3.10.3 highbit运算实现
- 3.10.4 扩展:取比给定值大的二进制位
- 3.10.5 扩展:取不小于给定值的二进制位
-
- 3.10.5.1 实现一
- 3.10.5.2 实现二
- 4. 位运算的应用
-
- 4.1 生成低N位掩码
- 4.2 生成从第M位开始的连续N位的掩码
- 4.3 取连续N位的值
-
- 4.3.1 先右移再取位,和先取位再右移有什么不同?
- 4.4 设置某些位的值
- 4.5 位连续翻转
- 4.6 lowbit应用:统计一个二进制数中为1的位数
- 4.7 lowbit应用:判断一个数是否是2的幂
- 4.8 lowbit应用:将右边第一组连续为1的二进制位变为0
- 4.9 将右边从最低位开始的连续为1的二进制位变为0
- 4.10 将右边从最低位开始的连续为0的二进制位变为1
- 4.11 奇偶判断
- 4.12 对 2 k 2^k 2k 取模
现代计算机中,几乎都是二进制计算机,所有的数据都以二进制的形式存储在设备中。位运算就是直接对存储在内存中的数据的二进制位进行操作。
在计算机中,每一个二进制位称为1个bit,单位简写做 b。通常8个bit为一个单位,称为 字节(byte),单位简写作 B。
一个字节不一定是8位,由硬件决定。但现在通用的标准中,一个字节等于8位。
在C/C++中表示二进制数一般使用0x前缀表示的十六进制形式,和二进制数有一一对应的关系,如0x5A,表示二进制数 01011010 0101 1010 01011010。
八进制属于废弃没人用的状态,八进制一个数占3位,和一个字节8位的现状格格不入,而利于显示二进制位的二进制格式却缺失,不得不说这是一种设计上的缺陷。Python及Java等由类C编程语言在早年就添加了二进制字面量,C++中二进制字面量直到C++14标准才补上,以 0b 或 0B表示,如 0b01011010,但C语言标准一直没有,只在GNU C编译器上有相应的扩展语法,所以在代码中以0b为前缀的数有可能编译不过。
1. 常见的位运算
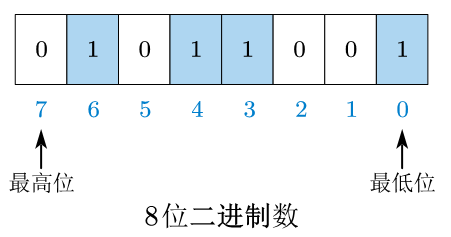
在 n n n 位二进制数中,我们一般称最低位为第 0 0 0位,最高位为 n − 1 n-1 n−1位,总右到左依次是第 0 , 1 , 2 , ⋯ , n − 1 位 0, 1, 2, \cdots, n-1位 0,1,2,⋯,n−1位,如下图所示:
我们在计算时,一般使用的是 32位的int 类型(在个人计算机中,int一般为32位),但为了便于将算法以图形表示,下面一般使用8位的二进制数来展示,而不是使用32位,否则位数太多,图形过小,不利于绘制和阅读。
在编程语言中,以下四个算术位运算最为常见:
| 与 | 或 | 非 | 异或 | |
|---|---|---|---|---|
| 运算符 | & | | | ~ | ^ |
| 英文表示的运算符 | and | or | not | xor |
1.0 位运算与逻辑运算之间的关系
逻辑运算也叫布尔运算,以逻辑中的真和假作为运算单元(布尔值)进行运算,运算结果也是真或假。在二进制中,一般用 1 和0 分别表示真和假。
位运算是将每个二进制位作为 布尔值,分别对一个或两个二进制数中对应的二进制位做布尔运算。如果是对两个数做运算,那么对应的两个二进制位一共有 00, 01, 10, 11四种组合,如果只对一个数做运算,那么二进制位只有0和1两种组合。对应位运算的结果仍然是布尔值,为 0 或 1。
需要注意,位运算是针对 二进制 的运算,分别对每一个二进制位进行布尔运算操作。所以在手动进行 位运算计算 时,需要将数转换成二进制的表示形式,再进行计算。如 3 & 5,先写成二进制形式的 0011 0011 0011 和 0101 0101 0101,右边最低位对齐后再分别对相应位进行位运算。
1.1 按位与
在 逻辑与 运算中,参与运算的两个布尔值只有 0 和 1 两种取值,只有当两个布尔值都为1时,结果才得1,其余只要有一个值为0,结果就为0,类似乘的关系。逻辑与 的符号为 &&。
| a | b | 逻辑与 | 结果 |
|---|---|---|---|
| 0 | 0 | 0 && 0 | 0 |
| 0 | 1 | 0 && 1 | 0 |
| 1 | 0 | 1 && 0 | 0 |
| 1 | 1 | 1 && 1 | 1 |
特性,和 1 相与不变,和 0 相与 得 0:
x & & 1 = x x & & 0 = 0 \begin{aligned} x\ \&\& \ 1 &= x \\ x\ \&\& \ 0 &= 0 \end{aligned} x && 1x && 0=x=0
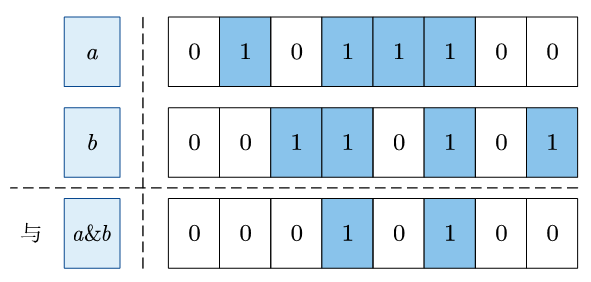
按位与 则是对两个二进制数的对应位分别做 逻辑与 运算,运算符号为 &。
从上面可以看到,与1相与不变,与0相与会变为0。可以利用这个特性将某些位清零,也可以取出某些位。
1.2 按位或
在 逻辑或 运算中,参与运算的两个布尔值只有 0 和 1 两种取值,只有当两个布尔值都为0时,结果才得0,其余只要有一个值为1,结果就为1,类似加的关系(不进位),逻辑或的符号为 ||。
| a | b | 逻辑或 | 结果 |
|---|---|---|---|
| 0 | 0 | 0 || 0 | 0 |
| 0 | 1 | 0 || 1 | 1 |
| 1 | 0 | 1 || 0 | 1 |
| 1 | 1 | 1 || 1 | 1 |
特性,和 1 相或 得 1,和 0 相或不变:
x ∣ ∣ 1 = 1 x ∣ ∣ 0 = x \begin{aligned} x \ | | \ 1 &= 1 \\ x \ ||\ 0 &= x \end{aligned} x ∣∣ 1x ∣∣ 0=1=x
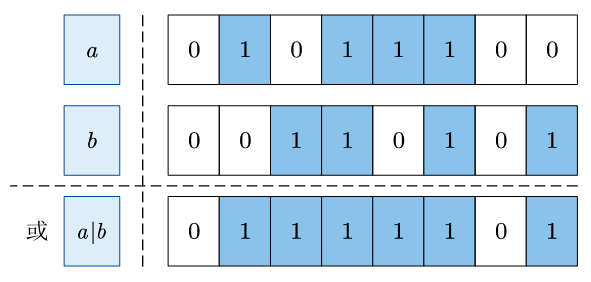
按位或 则是对两个二进制数的对应位分别做 逻辑或 运算,符号为 | 。
从上面可以看到,与1相或会变为1,与0相或不变。可以利用这个特性将某些位置位(位的值变为1)。
1.3 按位取反
在 逻辑非 运算中,布尔值只有 0 和 1 两种取值,当布尔值为0时结果为1,当布尔值为1时结果为0,逻辑非的符号为 !。
| a | 逻辑非 | 结果 |
|---|---|---|
| 0 | ! 0 | 1 |
| 1 | ! 1 | 0 |
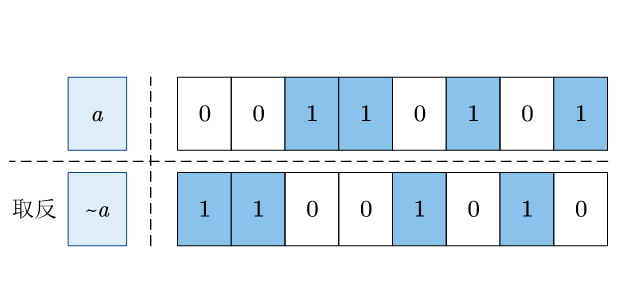
按位取反 即对二进制数的的每个位做 逻辑非 运算,原来是0的位变为1,原来是1的位则变为0, 符号为 ~,也叫 按位非。
1.4 按位异或
在 逻辑异或 运算 中,参与运算的两个布尔值只有 0 和 1 两种取值,只有当两个布尔值不同时,结果才得1,其余结果为0,类似不等于的关系,逻辑异或在数学上一般用符号 ⊕ \oplus ⊕ 表示。
在编程语言中很少有 逻辑异或 的符号,运算中一般用不等于(!=)替代,前提是参与运算的两个都是布尔值。
| a | b | 逻辑异或 | 结果 |
|---|---|---|---|
| 0 | 0 | 0 ⊕ \oplus ⊕ 0 | 0 |
| 0 | 1 | 0 ⊕ \oplus ⊕ 1 | 1 |
| 1 | 0 | 1 ⊕ \oplus ⊕ 0 | 1 |
| 1 | 1 | 1 ⊕ \oplus ⊕ 1 | 0 |
特性,和 1 异或 取反,和 0 异或不变:
x ⊕ 1 = ! x x ⊕ 0 = x \begin{aligned} x \oplus1 &= \ !x \\ x \oplus 0 &= \ x \\ \end{aligned} x⊕1x⊕0= !x= x
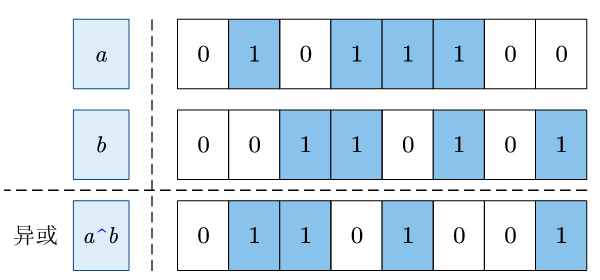
按位异或 则是对两个二进制数的对应位分别做 逻辑异或 运算, 符号为 ^。
从上面可以看到,与1异或会取反(由1变0,或由0变1),与0异或不变。可以利用这个特性将某些位取反。
按位异或可以将某些位取反,而取反两次则会变为原值: a ^ b ^ b = a a \text{\textasciicircum} b \text{\textasciicircum} b = a a^b^b=a
利用这个特性可以将因进行了按位异或而被改变的数据还原。
1.5 移位
1.5.1 左移
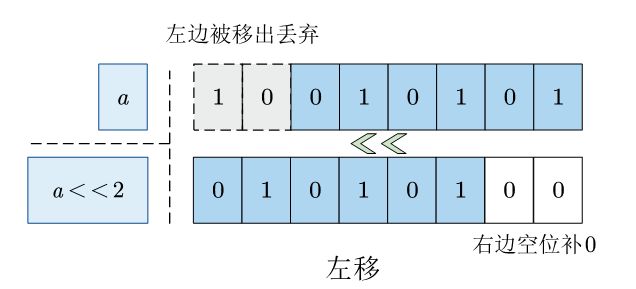
左移是将所有二进制位向左移动 n n n 位(对于32位值 n n n范围是 [ 0 , 31 ] [0, 31] [0,31])。移动后,最左边的 n n n 个二进制位将因被移出边界而丢弃,移动后最右边空出来的二进制位补0。
对于32位的int型值,如果移动位数超出 32 32 32 位,将会被对 32 32 32取模,如移动 35 35 35 位,将变成移动 3 3 3 位( 35 % 32 = 3 35\%32 =3 35%32=3)。所以左移 32 32 32位并不会变为 0 0 0,而是相当于移动 0 位,值不变。
对于 64 64 64位数,移动的位数则是对 64 64 64取模。
在没有发生 溢出 和 环绕 的情况下, n n n 左移一位后的值相当于 2 n 2n 2n。 n < < 1 = 2 n n<<1=2n n<<1=2n
溢出:指的是计算结果超出有符号数存储的范围。
环绕:指的是计算结果超出无符号数存储的范围。
例如,0b0101左移一位变成0b1010,由5变成10。
1.5.2 有符号右移(算术右移)
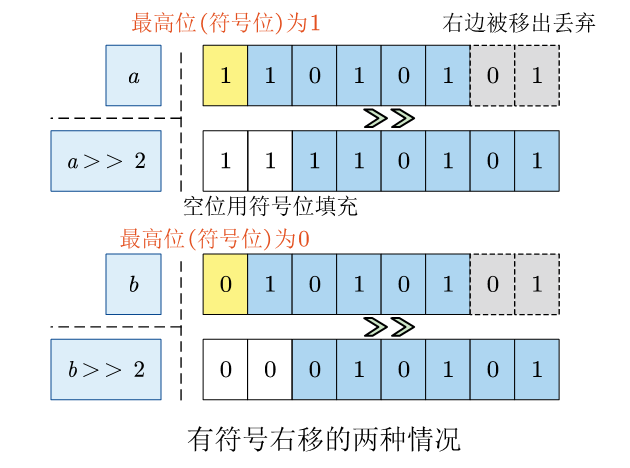
有符号整数左边的最高位为符号位,代表着数的正负,负数最高位为1,正数和0的最高位为0。有符号数右移时,最右边的位丢弃,最左边的空位补上原来的最高位。有符号右移又叫 算术右移,在算术上相当于是值除以2的结果,C/C++中对有符号类型变量的右移是算术右移。
如果移动位数超出 32 32 32 位,将会被对 32 32 32取模,如移动 35 35 35 位,将变成移动 3 3 3 位( 35 % 32 = 3 35\%32 =3 35%32=3)。所以右移 32 32 32位并不会变为 0 0 0 或 − 1 -1 −1 ,而是相当于 1 > > 0 1>>0 1>>0,值不变。对于更大的64位数,则是对64取模。
对于有符号数来说,算术右移的结果等于原数除以2再向下取整(公式中, ⌊ x ⌋ \lfloor x\rfloor ⌊x⌋为对 x x x向下取整):
n > > 2 = ⌊ a 2 ⌋ n >>2 =\lfloor \frac{a}{2} \rfloor n>>2=⌊2a⌋ 如负数 − 3 > > 1 = − 2 -3 >>1=-2 −3>>1=−2, 正数 3 > > 1 = 1 3>>1=1 3>>1=1。
负数不断进行算术右移,最终变为 − 1 -1 −1, 而非负数最终变为 0 0 0。
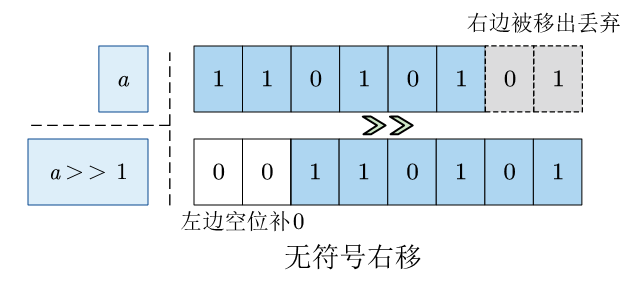
1.5.3 无符号右移(逻辑右移)
无符号数没有符号位,所有位都作为二进制的数值位。右移时,最右边的位丢弃,最左边的位补0。无符号右移又叫 逻辑右移。C/C++中对无符号类型变量的右移是逻辑右移。
如果移动位数超出 32 32 32 位,将会被对 32 32 32取模,如移动 35 35 35 位,将变成移动 3 3 3 位( 35 % 32 = 3 35\%32 =3 35%32=3)。所以右移 32 32 32位并不会变为 0 0 0,而是相当于 1 > > 0 1>>0 1>>0,值不变。对于更大的64位数,则是对64取模。
对于无符号数来说,算术右移的结果等于原数除以2再向下取整(公式中, ⌊ x ⌋ \lfloor x\rfloor ⌊x⌋为对 x x x向下取整):
n > > 2 = ⌊ a 2 ⌋ n >>2 =\lfloor \frac{a}{2} \rfloor n>>2=⌊2a⌋ 如 3 > > 1 = 1 3>>1=1 3>>1=1。
二进制数连续进行逻辑右移,最终变为 0 0 0。
2. 编程语言相关
2.1 位运算操作符
位运算主要有以下几种:
| 位运算 | C语言操作 | Java操作 |
|---|---|---|
| 按位与 | a & b | a & b |
| 按位或 | a | b | a | b |
| 按位异或 | a ^ b | a ^ b |
| 按位取反 | ~a | ~a |
| 左移 | a << b | a << b |
| 有符号右移 | a >> b(当变量 a 为有符号类型时) | a >> b |
| 无符号右移 | a >> b(当变量 a 为无符号类型时) | a >>> b |
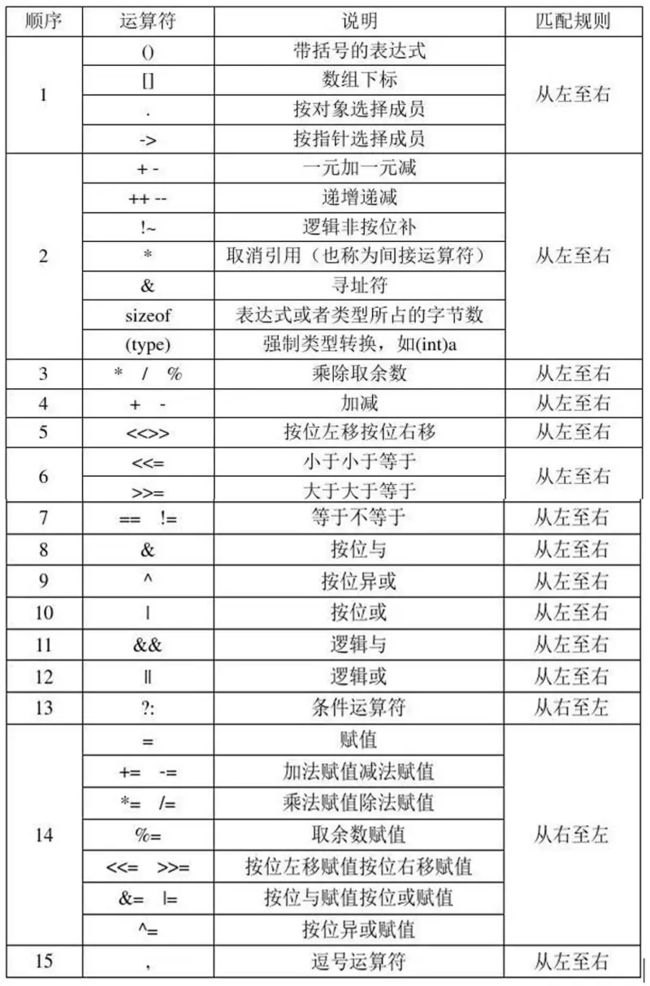
2.2 C运算符优先级
需要注意的是,除了一元运算符按位取反(~)外,其它位运算符的优先级都比较低,所以在计算时需要注意。除了加减和乘除、单目运算符和双目运算符、赋值运算符与其它运算符这种非常明显的优先级对比外,其它容易产生混淆的尽量用括号括起来,保证计算的顺序,而不是依赖于运算符的优先级,否则当自己记错或回忆不起时,就很容易影响到程序的正确性和可读性。
| 表达式 | 容易误认为的运算顺序 | 实际运算顺序 |
|---|---|---|
a & b != 0 |
(a & b) != 0 |
a & (b != 0) |
1 << 2 + 1 |
(1 << 2) + 1 |
1 << (2 + 1) |
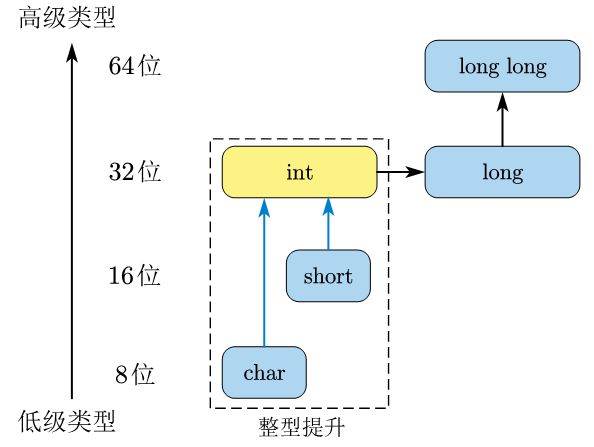
2.3 整数类型之间的转换
C/C++ 中的整数类型有 char, short, int, long 和 long long,这里按类型的位数进行区分,类型的位数越高,那么取值范围就越大,类型就越高级。
这里的类型等级不区分是有符号还是无符号,如果要区分的话,同一个整数类型的无符号类型相当于比有符号类型高半个等级。
当然,一个变量的类型无论是有符号还是无符号,其 存储的二进制内容都是不变的,不同的对这些二进制位的解释方法。无符号数把最高位作为一个普通的位,而有符号数把最高位作为符号位,相当于改变了最高位的权重。 n n n 位无符号数最高位权重是 2 n − 1 2^{n-1} 2n−1,而有符号数最高位权重是 − 2 n − 1 -2^{n-1} −2n−1。
如一个八位的无符号数 a a a,二进制表示为 1000 0001 1000\, 0001 10000001,最高位权重是128,最低位权重是1,因此值为 129。当把 a a a 转成有符号数时,二进制表示依然为 1000 0001 1000\, 0001 10000001,但此时最高位的含义已经发生了变化,相当于权重 − 128 -128 −128,此时值为 − 127 -127 −127。
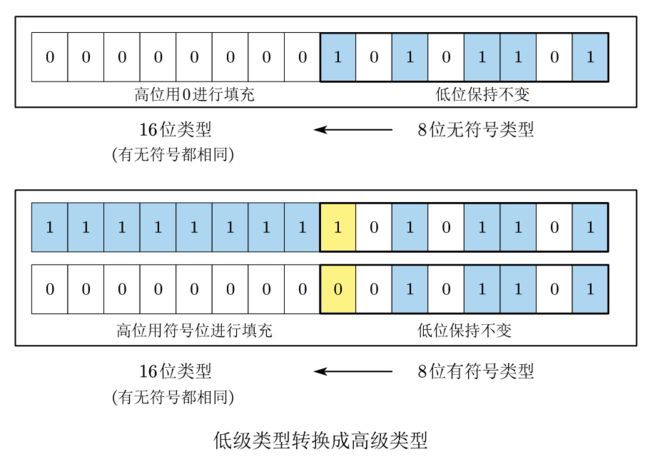
2.3.1 低级类型向高级类型转换
在整数类型之间的转换中,如果一个变量由 低级类型 向 高级类型 转换,那么转换时低位不变、高位根据变量 原先的类型 是无符号还是有符号使用不同的方式进行填补。
| 变量原先的类型 | 高位填补方式 |
|---|---|
| 无符号类型 | 用 0 填补 |
| 有符号类型 | 用符号位进行填补 |
2.3.2 高级类型向低级类型转换
在整数类型之间的转换中,如果一个变量由 高级类型 向低级类型转换,那么二进制位将会被 截断 ,高位丢弃,只保留低位作为转换后的二进制内容。最后的值是多少则根据转换后是有符号类型还是无符号类型对二进制位进行解析。
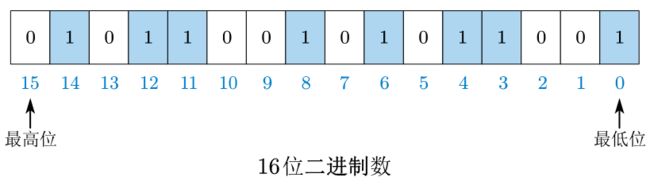
如下图所示,一个16位类型的值转成8位类型,直接截取低8位作为转换后的二进制内容 1010 1101 1010 \, 1101 10101101,如果这个8位类型是无符号,那么数值为 173,如果是有符号类型,则是 -83。
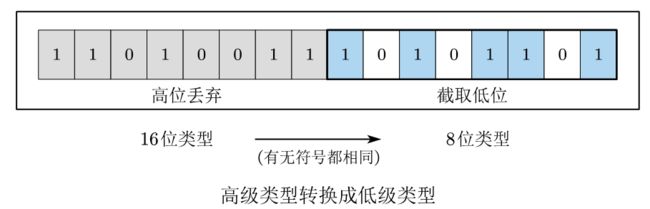
截断的方式实际上相当于将原值看作无符号类型然后进行取模。取模后得到一个无符号的二进制数,再根据转换后的类型是有符号还是无符号来确定最终的值。
应该知道的是,无论是有符号类型还是无符号类型,各个二进制位上的值都是一样的,只不过是赋予了最高位不同的含义。
2.3.3 整型提升
在C/C++中,进行表达式计算时,各种整数类型会首先自动转换成 int 型,如果 int 不足以表示的话,就需要提升为 unsigned int 类型,然后再执行表达式的运算。
因为 int 代表着CPU的自然运算类型,一个8位二进制数存储到32位寄存器中,高位也是会有数值的,所以会自然地扩展到32位。
这意味着即使参与运算的所有整数类型变量的类型都比 int 类型低级,在运算时也会先提升至 int型再运算,最终结果为 int型。如下所示,两个8位的 char 型的值 'A' 和 'B'进行运算时,会先转换成32位的 int 再进行计算,整个表达式结果为 int 型。
'A' + 'B'; // 表达式类型为 int
因此,虽然下面的表达式中三个变量都是 char 型,但是实际上发生两次 由 char 向 int 的转换,和一次由 int 向 char 的转换。
char a = 'A', b = 'B';
char c = a + b; // a 和b 在运算时会先转成 int,计算结果再由 int 转成 char 赋值给 c .
2.3.3.1 整型提升后的不同
那么,提不提升,结果有什么不同呢?在上面的表达式 char c = a + b中,提升和不提升最终结果不都是一样的吗?
① 如果变量先进行了整数提升,运算后再转换回原来的类型,那么结果是一样的,因为对最终值进行了截断,和原先溢出的结果是一致的。例如,char c = 'A' + 'B',被提升成 int 型后又被转换成 char 型,和不提升的结果是一致的。
② 如果变量先进行了整数提升,但不转换回原先的类型,那么结果就产生了不同。例如:
char a = 0xF0, b = 4;
//a 和 b 被提升至int型再运算
bool c = ((a << b) == 0);
printf("(a << b) = %#X, c = %d\n", (a << b), (int) c);
// 输出结果:(a << b) = 0XFFFFFF00, c = 0
a 和 b 都是 8位的char 型变量,如果不提升,那么如果按照左移的计算,a 左移4位后应该变为0 (高位被移出丢弃,低位补0),但是 a 被提升成 int 型后再左移,结果大大不同,变成了 0XFFFFFF00。这是因为 a 由 char 转换到 int ,变成0XFFFFFFF0,左移4位后为 0XFFFFFF00。所以 a << b 不等于 0, c 的值为 false。
3. 常用的位运算操作
3.1 二进制位 bit(n)
通常位运算是对 int 型进行操作,而其他类型如 char, short 等会先提升为 int 再运算。
一个字节共8位,最低位是第 0 0 0位,最高位是第 7 7 7位。如果是32位的 int 型,则最低位为第 0 0 0位,最高位为第 31 31 31位。
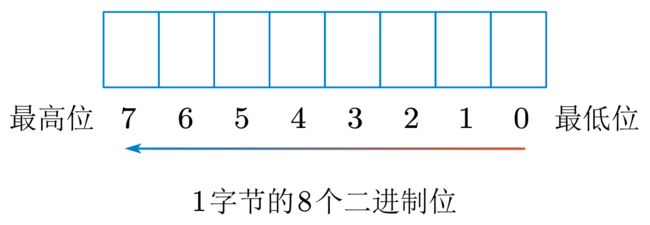
第 n n n位可以通过将 1 1 1 左移 n n n 位得到,如,第 7 7 7位为 1U << 7。
这里需要使用无符号的 1 1 1是因为,如果有符号数的第31位为1时,扩展到更高的64位时高32位会被1填充,由
0x80000000变成0xFFFFFFFF80000000,这就不符合要求了,所以生成的值类型应该是无符号数。当然,如果在使用时不考虑与64位的值进行运算,那么使用正常的有符号数即可。
inline unsigned int bit(unsigned int n)
{
return 1U << n;
}
或者以宏的形式进行定义:
#define bit(n) (1U << (n))
3.2 数二进制形式输出
在C语言中,printf()并不能直接将变量以二进制格式输出。已有的八进制和十六进制格式对于查看二进制数并不直观。为了可以方便查看二进制位的值,需要自行实现或者借助标准库函数。
3.2.1 itoa() 函数
标准库函数itoa() 能够将数值转换成 2~36进制格式的字符串,函数在头文件
我们可以借助 itoa() 函数来生成二进制格式字符串,然后使用 printf()将其输出。
#include itoa() 生成的字符串并不能固定位数,所以如果想输出固定位数的二进制形式,可以在字符串前输出相应个数的0,手动补齐位数。
// 输出二进制数, value:值, nBit:二进制数的位数
void printfBinary(int value, unsigned int nBit)
{
char buffer[33];
_itoa(value, buffer, 2);
size_t len = strlen(buffer);
//计算需要填充的空位数,如果设置的位数不比实际大,则填充数为0
size_t fillNum = (nBit >= len) ? (nBit - len) : 0;
printf("0b");
//填充字符'0'
while (fillNum-- > 0) {
printf("0");
}
//输出原字符串
printf("%s", buffer);
}
3.2.2 手动实现二进制格式的输出
将对应的二进制位提取出来并输出,4个为一组,用空格间隔,增加可读性。
void printBinary(unsigned int num, int nBit)
{
if (nBit > 32 || nBit <= 0)
nBit = 32;
for (unsigned int n = nBit; n-- > 0; ) {
putchar((((num >> n) & 1) == 0) ? '0' : '1');
if (n % 4 == 0)
putchar(' ');
}
}
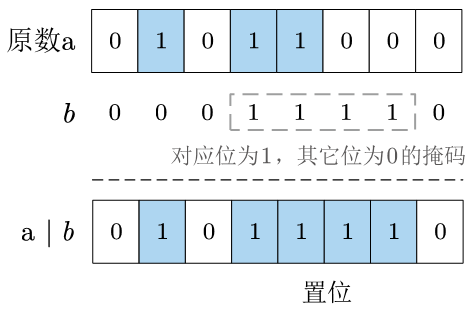
3.3 对应位置位
置位即将二进制位置为1。
利用位或运算 x ∣ 1 = 1 , x ∣ 0 = x x |1 = 1, x|0=x x∣1=1,x∣0=x 的特性,将原数和对应位和1位或,其它位和0位或的二进制数位或,即可将对应位置位。
例如,想要将第0位置为1,可以将原数与 0x01做位或运算
a | 0x01;
如果是想将第 n n n 位置1,则可以按如下操作
a = a | bit(n); //即 a = a | (1U << n);
简写为
a |= bit(n);
对多位同时置位,可以先将多个bit位或,然后再和原数位或。
a |= (bit(n1)| bit(n2) | bit(n3));
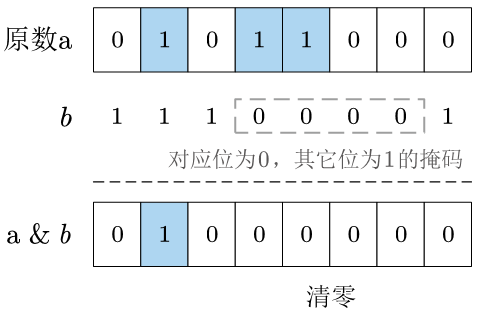
3.4 对应位清零
清零即将二进制位变为0。
若要将某一位清零, 可以利用位与运算 和1位于不变,和0位与得0 的特性,将原数与对应位为0,其它位为1 的二进制数位与即可。
对应位为0,其它位为1的码,可以通过将对应的二进制位取反得到 ~bit(n),如第0位为0,其余位为1的码:
~0x01 //假设为8位二进制数,0x01为 0000 0001,那么~0x01为 1111 1110
将第 n n n 位清零可以按如下操作:
a = a & ~bit(n);
简写为
a &= ~bit(n);
对多位同时清零,可以将多个bit位或。
a &= ~(bit(n1)| bit(n2) | bit(n3));
3.5 对应位取反
对应位取反 是利用 按位异或运算 (和1异或取反、和0异或不变) 的特性来进行的。
通过将原数 a a a 与 对应位为1、其它位为0)的 b b b 进行按位异或运算,将 a a a 中对应位取反的同时,还保持其它位不变 。
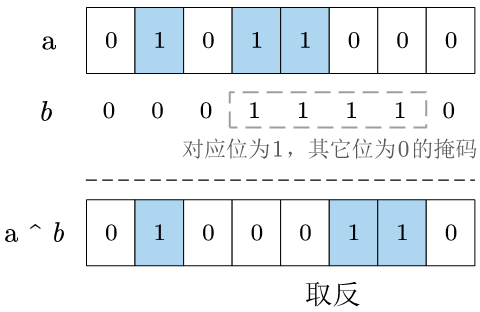
将二进制数的第 n n n 位取反,只需要将原数与第 n n n 位为1,其余为0的二进制数进行 按位异或运算 即可。
a = a ^ bit(n);
简写为:
a ^= bit(n);
对多个位同时取反,可以将多个二进制位用 位或 组合。
a ^= bit(n1) | bit(n2) | bit(n3);
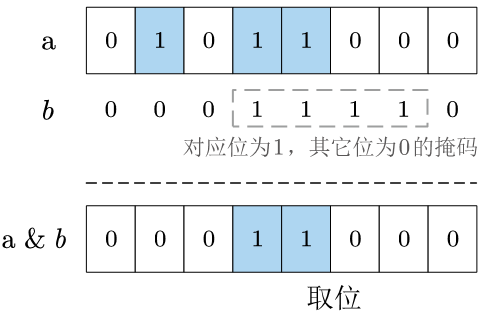
3.6 取二进制位
3.6.1 取二进制位
取位是利用位与运算 (和1位于不变,和0位与得0) 的特性来进行的,将对应位和1 位与来得到对应位的值。
(bit(n)为 1 << n,即第n位上为1,其余位为0的数)
//取第0位
a & bit(0)
//取第3位
a & bit(3)
如果想同时取多个位,可以通过将二进制数与对应位为1的数位与来得到对应位。这个数可以直接写,也可以使用 位或运算来构造,如取第0位、第1位和第7位,写成 bit(n0 异或的方式:
a & (bit(0) | bit(1) | bit(7))
//等价于
a & 0x83
示例:
//取低8位
a & 0xFF
//取第8至第15位
a & 0xFF00
//取高16位
a & 0xFFFF0000
//取偶数位
a & 0x55555555
3.6.2 取两个二进制数不同的位
直接用按位异或即可取出两个二进制数不同的位。
a ^ b
3.6.2 取a为1,b为0的位
取a为1,b为0的位
a & (~b);
或者先取差异位,再取位
(a ^ b) & a;
3.7 位逆序
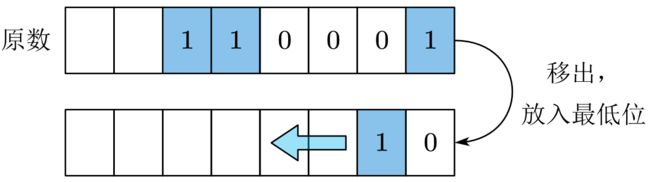
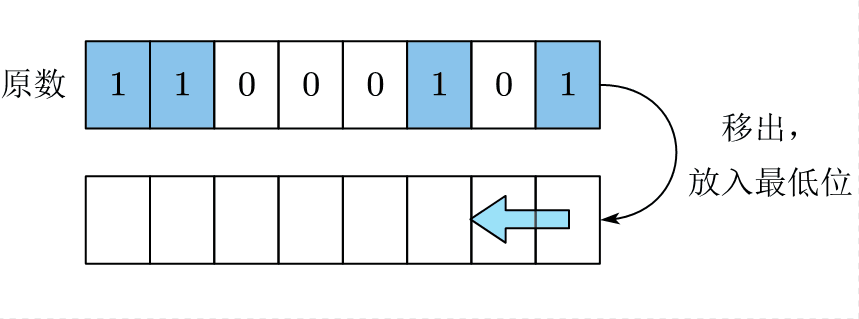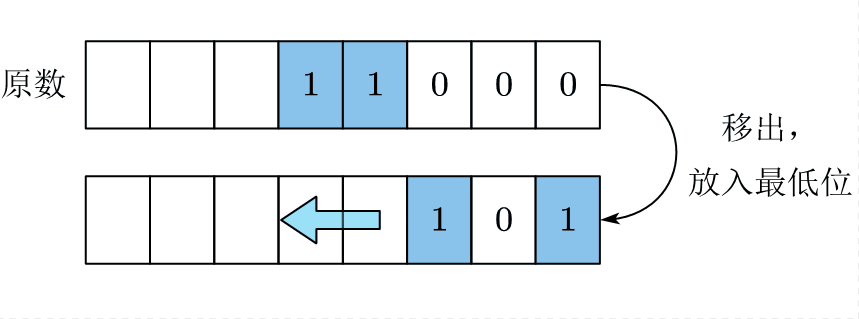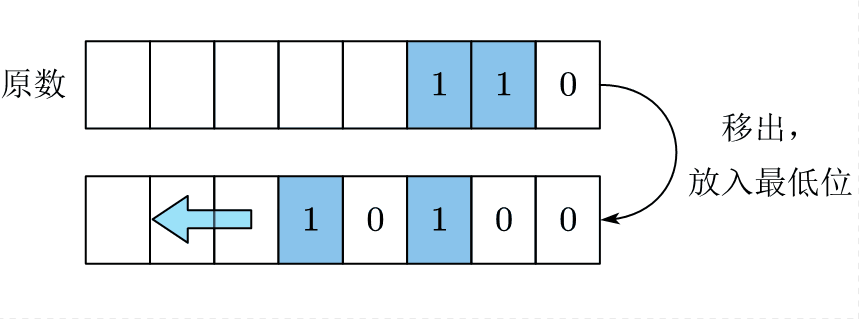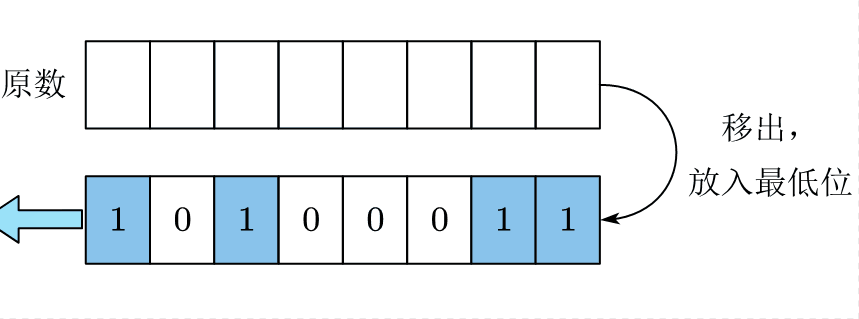
3.7.1 常规位逆序方法
步骤是不断地取出原数 a a a的最低位并将 a a a右移,然后将另一个初始值为0的数 b b b左移,并将从 a a a取出的最低位放到 b b b的最低位上。多次循环后,二进制位将被逆序,复杂度为 O ( N ) O(N) O(N)。
//二进制位逆序
//nBit为原数的位数,函数会截取num的低nBit位,逆序后返回
int bitReverse(int num, unsigned int nBit)
{
if (nBit > 32)
nBit = 32;
int ans = 0;
while (nBit-- > 0) {
ans <<= 1;
//将num的最低位取出放到ans的最低位上
ans |= num & 1;
num >>= 1;
}
return ans;
}
3.7.2 蝴蝶算法
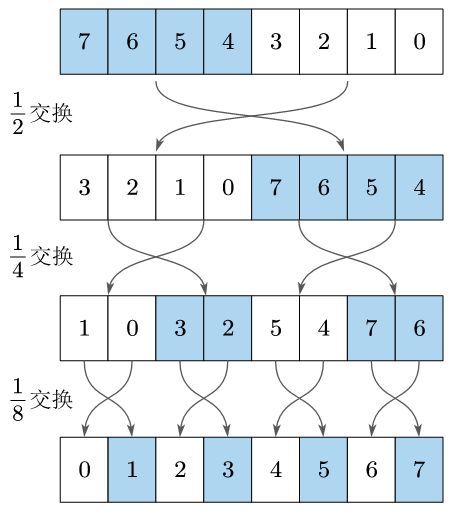
蝴蝶算法是通过递归将二进制位左右分半并进行交换来完成逆序的,如下图所示:
左右交换从位置上看,实际上是一部分左移,另一部分右移。往同一个方向移动的位都是移动相同的位数,因此可以把所有要左移的位一次性取出,然后移位即可,右移也是同样的操作,最后再使用位或将两部分合并。所以一次交换一步即可完成。
如8位二进制数的第一次的 1 2 交换 \dfrac{1}{2}交换 21交换, 只需要如下操作即可:
((num >> 4) & 0x0F) | ((num << 4) & 0xF0)
其中 0x0F 和 0xF0 是用于配合 位与(&) 取对应的二进制位,称为掩码。
也可以先取对应二进制位再移动,但是这样要保证num为无符号整数,否则当最高位为1时,右移可能会引入多余的1,所以并不推荐先取位再移动。
((num & 0x0F) << 4) | ((unsigned int)(num & 0xF0) >> 4)
逆序算法中的位交换也可以反着顺序来,先以1位为一组,交换相邻两组,再以两位为一组相互交换,再以四位为一组进行交换,直至所有位都为一组。
3.7.2.1 8位二进制数逆序
8位二进制数的逆序算法如下,属于常用且较为简单的算法,可以直接使用固定数值来简化加速:
掩码的变化依次为:
0b11110000, 0b00001111
0b11001100, 0b00110011
0b10101010, 0b01010101
unsigned char byteReverse(unsigned char data)
{
data = ((data<<4) & 0xF0) | ((data>>4) & 0x0F);
data = ((data<<2) & 0xCC) | ((data>>2) & 0x33);
data = ((data<<1) & 0xAA) | ((data>>1) & 0x55);
return data;
}
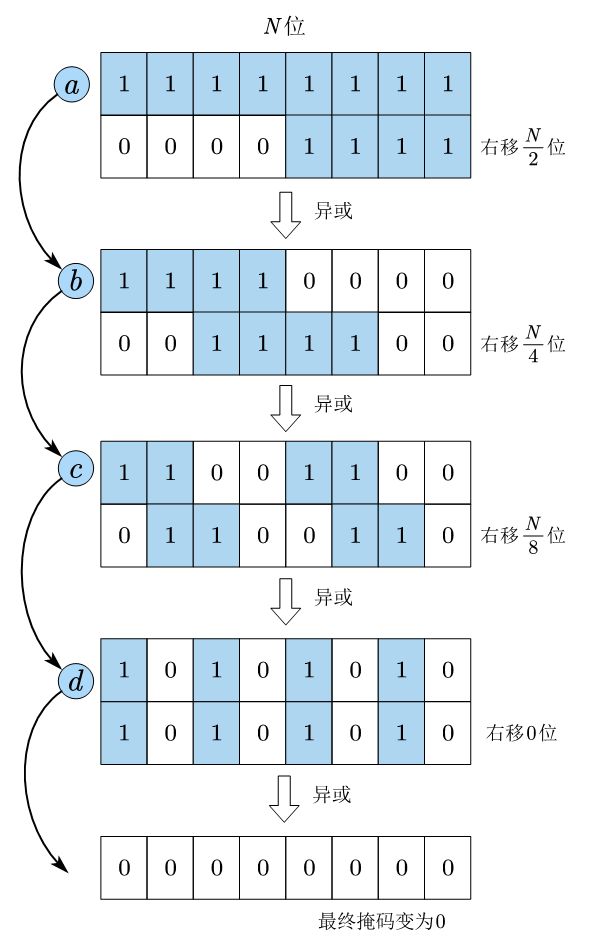
3.7.2.2 N N N 位二进制数逆序
N N N 位的蝴蝶算法(N只能取2的幂,如32,16, 8等,否则中间无法等分。 int 是32位的,所以 N N N 最大为32)
最重要的是如何构造出要移动的位对应的二进制掩码。我们只需将原来 M M M位连续的掩码右移 M 2 \dfrac{M}{2} 2M位,再与原来的掩码按位异或即可得到下一级的掩码。
算法实现如下,复杂度为 O ( log n ) O(\log n) O(logn)。
unsigned int bitReverse(unsigned int num, unsigned int N = 32)
{
//先构造低N位的掩码
unsigned int mask = (N >= 32) ? (0xFFFFFFFF) : ((1U << N) - 1U);
num &= mask; //取低N位
unsigned int M = N / 2; //生成下一级掩码需要移动的位数
// 当M=0时,下一级掩码将为全0,此时已逆序完成,可以结束
while (M > 0) {
//构造每一组中高为1,低为0的位掩码
mask ^= (mask >> M);
//每组对半交换
num = ((num << M) & mask) | ((num >> M) & ~mask);
M /= 2;
}
return num;
}
掩码为全0后就已经逆序完成,而且值就不再变化,所以循环至掩码为 10101010 10101010 10101010 即可。
3.8 位循环移动
位循环移动即相当于把所有位看成一个首尾相连的环,一端移出的位会放入另一端。
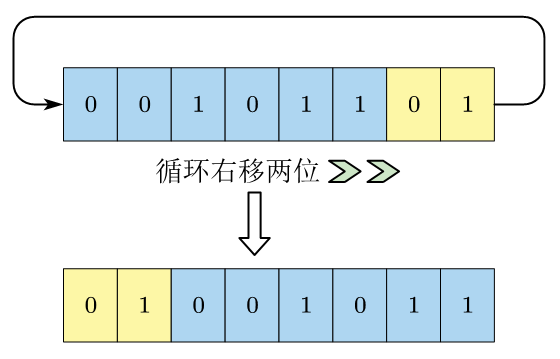
位循环移动 n n n位,相当于将所有位分割左右两部分,一部分 n n n位,另一部分为 N − n N-n N−n位( N N N为二进制数的总位数),然后左右对调。因此,我们分别将两部分移动至对应位置上即可。
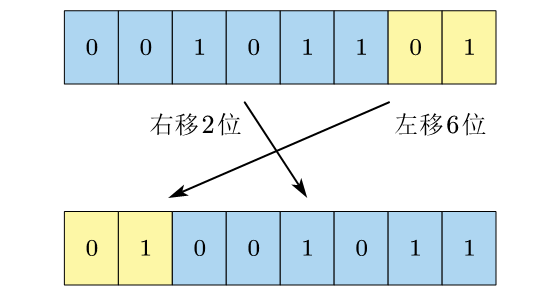
因为无符号数的左移和右移,空位都会被补上0,所以移位后并不需要进行取位,直接左移或右移就能得到对应的位。最后再通过按位或运算将两部分组合起来即可。
对于32位的unsigned int型变量,移动的位数可以对32求余,然后分别移动 n n n 位和 32 − n 32-n 32−n 位,写法如下所示:
//将32位数num循环右移n位
unsigned int circleRightShift(unsigned int num, unsigned int n)
{
n %= 32;
return (num >> n) | (num << (32 - n));
}
//将32位数num循环左移n位
unsigned int circleLeftShift(unsigned int num, unsigned int n)
{
n %= 32;
return (num << n) | (num >> (32 - n));
}
上面是固定的位数,如果想设置对于8位二进制数,16位二进制数或者其它32位以下其它数,可以再加一个总位数的参数。
需要注意的是,之前固定位数的移动,空位会自动补0,但现在设置的位数和变量类型实际上不匹配,所以并不会帮你补零,所以在计算前需要将其它位手动清0。并且计算完成后,需要再一次将其它位清零,否则数据会移动至其他高位上。
//将nBit位二进制数num循环右移n位
unsigned int circleRightShift(unsigned int num, unsigned int n, unsigned int nBit)
{
if (nBit > 32)
nBit = 32;
//获取低nBit位的掩码
unsigned int mask = (nBit >= 32) ? (0xFFFFFFFF) : ((1U << nBit) - 1U);
num &= mask; //取低nBit位
n %= nBit;
return ((num >> n) | (num << (nBit - n)) ) & mask;
}
//将nBit位二进制数num循环左移n位
unsigned int circleLeftShift(unsigned int num, unsigned int n, unsigned int nBit)
{
if (nBit > 32)
nBit = 32;
//获取低nBit位的掩码
unsigned int mask = (nBit >= 32) ? (0xFFFFFFFF) : ((1U << nBit) - 1U);
num &= mask; //取低nBit位
n %= nBit;
return ((num << n) | (num >> (nBit - n)) ) & mask;
}
3.9 lowbit运算
l o w b i t lowbit lowbit 运算 是位运算中比较重要的运算方式,用于计算一个二进制数最低位的1。
3.9.1 lowbit概念
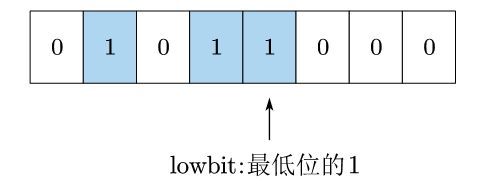
l o w b i t \mathrm{lowbit} lowbit 即二进制数最低位1所对应的值。
如,二进制数 0 b 01011000 \mathrm{0b01011000} 0b01011000最低的 1 1 1是在第 3 3 3位,对应值为 0 b 1000 \mathrm{0b1000} 0b1000。
我们把数用二进制的形式来表示,如下(左为十进制数,右为二进制数,二进制数用前缀 0 b \mathrm{0b} 0b): 2 = 0 b 00000010 5 = 0 b 00000101 160 = 0 b 10100000 \begin{aligned} 2 &= \mathrm{0b00000010} \\ 5 &= \mathrm{0b00000101} \\ 160 &=\mathrm{0b10100000} \end{aligned} 25160=0b00000010=0b00000101=0b10100000 在上面 2 2 2, 5 5 5和 160 160 160 的二进制表达式中,我们直接取最低位的1对应的二进制值,得到
l o w b i t ( 2 ) = 0 b 00000010 l o w b i t ( 5 ) = 0 b 00000001 l o w b i t ( 160 ) = 0 b 00100000 \begin{aligned} \mathrm{lowbit}(2) &= \mathrm{0b}00000010 \\ \mathrm{lowbit}(5) &= \mathrm{0b}00000001 \\ \mathrm{lowbit}(160) &= \mathrm{0b}00100000 \end{aligned} lowbit(2)lowbit(5)lowbit(160)=0b00000010=0b00000001=0b00100000
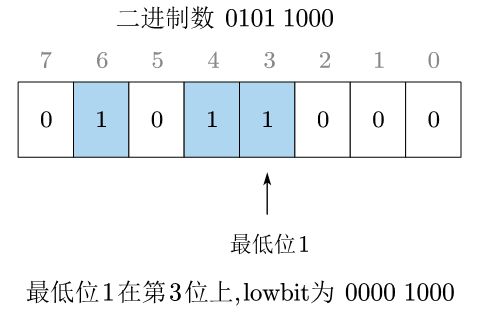
由上面的结果可以得出,假设一个数的二进制表示最低位的1在第 k k k位(从右往左,最右边为第0位),那么,这个数的 l o w b i t lowbit lowbit值为 2 k 2^{k} 2k。
如下图,最低位1在第3位上,则 l o w b i t lowbit lowbit 值为 2 3 = 8 2^3 = 8 23=8,也就是 0 b 1000 \mathrm{0b1000} 0b1000。
3.9.2 lowbit运算的实现
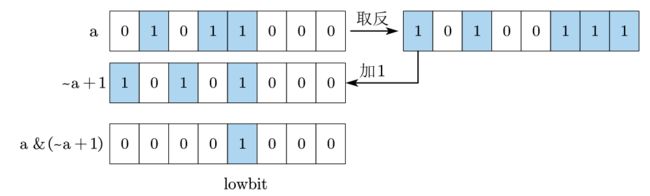
一个数的 l o w b i t \mathrm{lowbit} lowbit值,即一个数的最低位,可通过如下操作取出,复杂度为 O ( 1 ) O(1) O(1):
假设原来的数是a,对a取反加1得到~a+1,原数a和~a+1进行位与操作,就得到了 l o w b i t \mathrm{lowbit} lowbit值,即lowbit(a) = a & (~a + 1)。
int lowbit(int a)
{
return a & (~a + 1);
}
因为取反加1就是一个数的相反数的补码,lowbit也写作
int lowbit(int a)
{
return a & (-a);
}
当这个数是0,没有最低位1的时候,结果将为0。
所以求 l o w b i t ( a ) \mathrm{lowbit}(a) lowbit(a) 值的运算方法为: l o w b i t ( a ) = a & ( ∼ a + 1 ) = a & ( − a ) \mathrm{lowbit}(a)=a \ \& \ ( \sim a + 1)=a\ \& \ (-a) lowbit(a)=a & (∼a+1)=a & (−a)
3.9.3 消去lowbit
一个数消去它的 l o w b i t \mathrm{lowbit} lowbit 位,直接减去它的 l o w b i t \mathrm{lowbit} lowbit值 即可。由上面 l o w b i t \mathrm{lowbit} lowbit 的求法,可得:
int removeLowbit(int a)
{
return a - lowbit(a); //a - (a & -a)
}
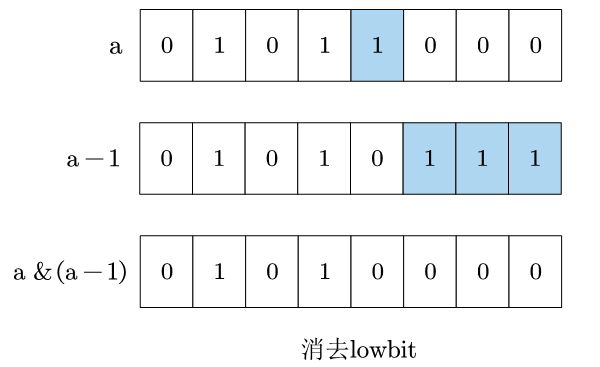
还可以由 a & (a-1) 得到:
int removeLowbit(int a)
{
return a & (a-1);
}
通过不断进行消除 l o w b i t \mathrm{lowbit} lowbit 操作,最后会变成0,并且 0 & (0-1) 依旧为 0。
既然得到了移除 l o w b i t \mathrm{lowbit} lowbit 后的二进制数,那么使用之前的值减去移除 l o w b i t \mathrm{lowbit} lowbit 后的值, 就得到了求 l o w b i t \mathrm{lowbit} lowbit 的另一种算法:
int lowbit(int a)
{
return a - (a & (a-1)); // a - removeLowbit(a);
}
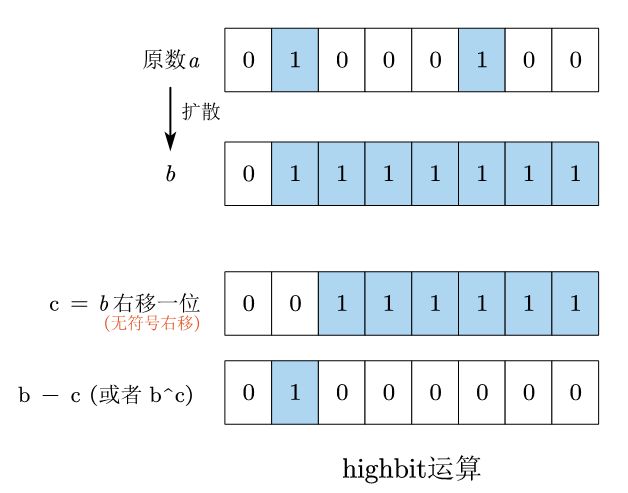
3.10 highbit运算
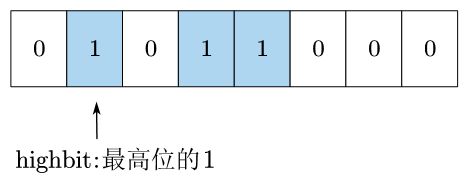
h i g h b i t \mathrm{highbit} highbit 即二进制数最高位1所对应的值。
如,二进制数 0 b 01011000 \mathrm{0b01011000} 0b01011000最高的 1 1 1是在第 6 6 6位,对应值为 0 b 01000000 \mathrm{0b01000000} 0b01000000。
h i g h b i t \mathrm{highbit} highbit 运算和 l o w b i t \mathrm{lowbit} lowbit 运算不同,并不能通过一个简单计算得到。一般是通过将最高位的1往低位扩散,直至填满比它低的位,再利用异或操作得到目标位。
这里先列出代码,方便后面解释。
//highbit运算,取最高位的1
unsigned int highbit(unsigned int n)
{
n |= (n >> 1);
n |= (n >> 2);
n |= (n >> 4);
n |= (n >> 8);
n |= (n >> 16);
// 如果考虑 int 是64位的情况,那么需要再扩散一次,32位数多扩散一次无影响
n |= (n >> 32);
return n ^ ((unsigned int)n >> 1);
}
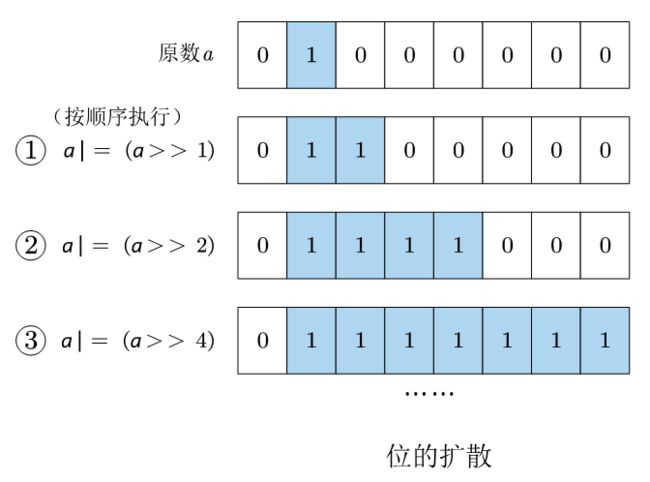
3.10.1 位的扩散
这里的核心操作就是位的“扩散”:将二进制数中比最高位1低的位全部变为1,采用的是右移和位或操作。
N N N位数完成扩散需要进行至 a |= (a >> (N/2)),如32位数需要进行至 a |= (a >> 16),8位数需要进行至 a |= (a >> 4)。多次扩散对变量值无影响,8位数也可进行至 a |= (a >> 16),因为位移会对位宽进行取模,取模后移位数为0,相当于不变。
扩散的复杂度是 O ( log log n ) O(\log \log n) O(loglogn),这个复杂度通常可视为 O ( 1 ) O(1) O(1),因为变量一般是32位或64位数,运算不超过6次。
// 将二进制数中比最高位1低的位全部变为1
unsigned int bitSpread(unsigned int a)
{
// 连续进行移位位或
a |= (a >> 1);
a |= (a >> 2);
a |= (a >> 4); // 8位
a |= (a >> 8); // 16位
a |= (a >> 16); // 32位
a |= (a >> 32); // 64位
return a;
}
3.10.2 利用异或取最高位
假设二进制数 a a a 的最高位1在第 k k k 位上,位扩散完成之后,整个数变成一个 0 ∼ k 0 \sim k 0∼k 位都为1的二进制数 b b b,再将其右移,进行 位异或 或者 相减即可得到最高位。
b ^ ((unsigned int) b >> 1U);
或者
b - ((unsigned int) b >> 1U);
注意这里 b >> 1 虽然是 0 ∼ k − 1 0 \sim k-1 0∼k−1 位都为1的二进制数,但是这里并不是通过加1来得到最高位,而是和 b b b 进行运算,这是因为如果出现 b = 0 b = 0 b=0的情况,(b >> 1)+1 将会得到错误的结果:1,正确结果应该是0。
3.10.3 highbit运算实现
最终得到如下的实现代码,如果 int 是32位数,执行至 n |= (n >> 16) 即可,如果考虑 64位的情况,那么需要多执行一步。
特别需要注意的是,下面的处理代码中,即使
n已经是无符号类型了,依然特意添加一个强转类型unsigned int,这是因为上面的n类型可以是有符号类型 ,但 这一步必须是无符号右移。
unsigned int highbit(unsigned int n)
{
n |= (n >> 1);
n |= (n >> 2);
n |= (n >> 4);
n |= (n >> 8);
n |= (n >> 16);
// 如果考虑 int 是64位的情况,那么需要再进行 n |= (n >> 32);
// 这里必须是无符号右移
return n ^ ((unsigned int)n >> 1);
}
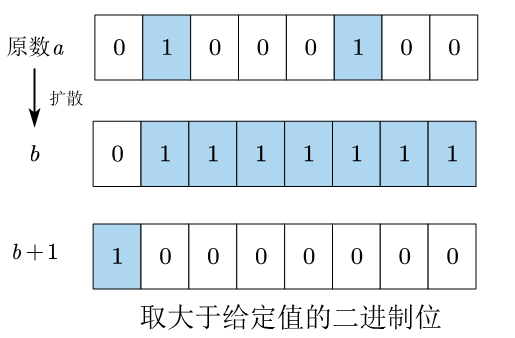
3.10.4 扩展:取比给定值大的二进制位
在将最高位扩散完成后,加1即可得到比给定值大的一个二进制位。
特殊情况就是二进制数的最高有效位为1(如32位数的第31位为1),那比它更大的二进制位是无法表示的,32位数没有第32位。如果最高有效位为1,那么扩散后所有位都会变为1,再加1会变为0。可以根据结果是否为0判断是否出现溢出的情况。
// 将二进制数中比最高位1低的位全部变为1
unsigned int bitSpread(unsigned int a)
{
// 连续进行移位位或
a |= (a >> 1);
a |= (a >> 2);
a |= (a >> 4); // 8位
a |= (a >> 8); // 16位
a |= (a >> 16); // 32位
a |= (a >> 32); // 64位
return a;
}
// 计算比n大的二进制位,如果32位数或64位数的最高有效位为1,结果为0
unsigned int largerPowOfTwo(unsigned int n)
{
return bitSpread(n) + 1U;
}
3.10.5 扩展:取不小于给定值的二进制位
3.10.5.1 实现一
在 3.10.4中,只能得到比给定值大的二进制位,如果想在给定值本身已经是二进制位时,直接返回原值,可以做一下处理:
① 先判断原值是否是2的幂(利用 lowbit 运算),是2的幂直接返回
② 不是2的幂则按 3.10.4的方法进行处理。
// 判断数是否是2的次幂
bool isPowerOfTwo(unsigned int a)
{
// 原数不等于0,且消去lowbit后等于0,即二进制位只有一个1
return (a != 0) && ((a & (a-1)) == 0)
}
// 将二进制数中比最高位1低的位全部变为1
unsigned int bitSpread(unsigned int a)
{
// 连续进行移位位或
a |= (a >> 1);
a |= (a >> 2);
a |= (a >> 4); // 8位
a |= (a >> 8); // 16位
a |= (a >> 16); // 32位
a |= (a >> 32); // 64位
return a;
}
// 返回大于或等于 n的最小的一个二进制位
// 如果二进制位超出表示范围,则返回0
unsigned int nearestPowOfTwo(unsigned int n)
{
if (isPowerOfTwo(n))
return n;
else
return bitSpread(n) + 1U;
}
3.10.5.2 实现二
位扩散后再加1的得到的值是比给定值大的二进制位,我们可以先将原数减1后再进行处理,这样就可以在给定值本身是二进制位时返回原值。
将原数减1后再计算,结果超出范围时会溢出变为0,这个是合理的。但是如果原数为0,计算后得到0 (0不是2的幂,1才是),这是不符合要求的,需要做特殊处理。
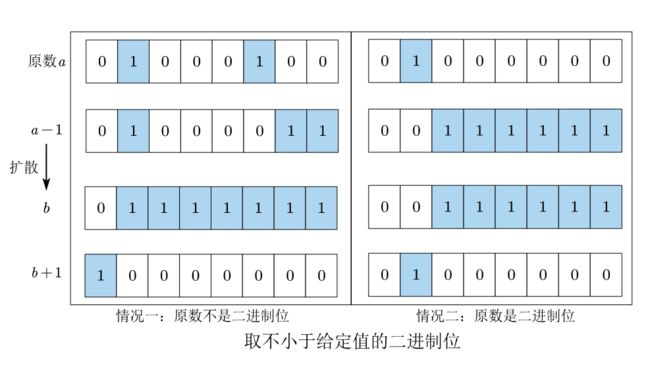
// 将二进制数中比最高位1低的位全部变为1
unsigned int bitSpread(unsigned int a)
{
// 连续进行移位位或
a |= (a >> 1);
a |= (a >> 2);
a |= (a >> 4); // 8位
a |= (a >> 8); // 16位
a |= (a >> 16); // 32位
a |= (a >> 32); // 64位
return a;
}
// 返回大于或等于 n的最小的一个二进制位
// 如果二进制位超出表示范围,则返回0
unsigned int nearestPowOfTwo(unsigned int n)
{
if (n == 0U)
return 1U;
else
return bitSpread(n-1) + 1U;
}
可以对上面的bitSpread()函数 和 nearestPowOfTwo() 函数进行整合,得到一个函数
// 返回大于或等于 n的最小的一个二进制位
// 如果二进制位超出表示范围,则返回0
unsigned int nearestPowOfTwo(unsigned int num)
{
unsigned int n = num - 1;
n |= (n >> 1);
n |= (n >> 2);
n |= (n >> 4); // 8位
n |= (n >> 8); // 16位
n |= (n >> 16); // 32位
n |= (n >> 32); // 64位
return (num == 0U) ? 1U : (n + 1U);
}
4. 位运算的应用
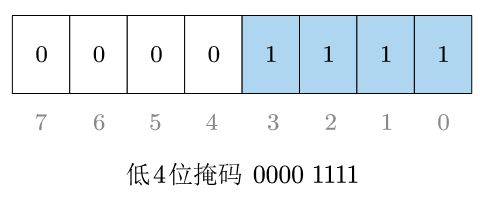
4.1 生成低N位掩码
低 N N N位掩码的值等于 2 N − 1 2^{N}-1 2N−1,如低8位掩码 0xFF 的值为 255 255 255,等于 2 8 − 1 2^{8}-1 28−1,而 2 N 2^{N} 2N可以通过 1 << N 得到,所以可以通过(1 << N) - 1来求取:
unsigned int mask(unsigned int n)
{
return (n >= 32) ? (-1) : ((1U << n) - 1);
}
需要注意的是,二进制位全为1的值为 0xFFFFFFFF,即 (0 - 1),但是移位会对32取模,1 << 32 的值为 1 << 0,即1,并非为0,所以需要特殊处理。
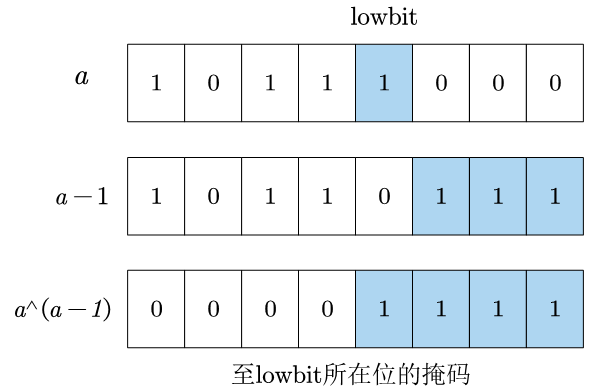
如果一个二进制数 a a a 的 l o w b i t \mathrm{lowbit} lowbit 在第 N N N位,想要生成低 N + 1 N+1 N+1位的掩码,可以通过 a ^ (a-1) 得到。但需要注意0的特殊情况,0^(-1)为全1,实际应返回0。
unsigned int maskToLowbit(unsigned int a)
{
return (a == 0) ? 0 : (a ^ (a-1));
}
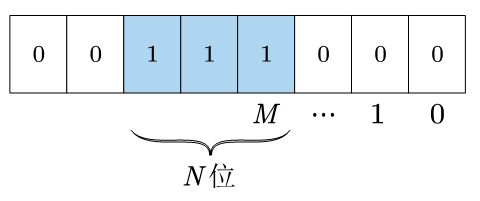
4.2 生成从第M位开始的连续N位的掩码
可以通过将低 N N N位掩码左移 M M M位得到,例如0b00000111 左移4位变成 0b00111000。
而低 N N N位掩码可以借用上面的
mask()函数 生成,对于固定的某些位可以直接用固定值。
示例:
生成16位数中高字节的掩码(即第8至第15位)。
0XFF00
或 (0xFF << 8)
或 mask(8) << 8
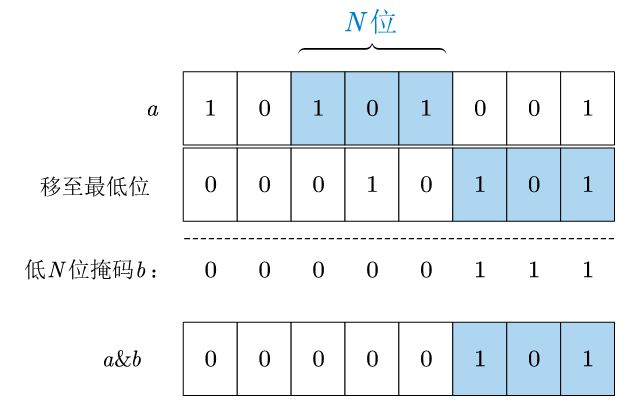
4.3 取连续N位的值
如果连续的 N N N 位是从第 n n n 位开始,可以通过将二进制数 右移 n n n 位来将对应位移至最低位,再和低 N N N 掩码位与 就可以得到对应位的值。
示例:
取32位数中第三个字节的值。第三个字节从第24位开始的8位,所以可以将原数右移24位,然后和低8位掩码0xFF 做 按位与运算 即可得到对应的值。
(a >> 24) & 0xFF;
4.3.1 先右移再取位,和先取位再右移有什么不同?
先移位再取位可以不用考虑原来的值是无符号类型还是有符号类型,但先取位再右移的方式需要考虑。
如果是先对原来的数 num 取位再移位,要保证num为无符号整数,否则当num最高位为1时,移动就会引入多余的位。
例如,对于有符号8位二进制数 0b11000001,想要取高4位的值,应该得到 0b00001100。
- 如果是先取高4位再右移4位,会变成
0b11111100,高位被填补上1,这并不是想要的结果,如果想要不被填补上1,那就得先把 num 转换成无符号数再右移。
//有符号数和无符号数结果的不同
int8_t num = 0b11000001;
(num & 0xF0) >> 4; //得到 0b11111100
uint8_t num = 0b11000001
(num & 0xF0) >> 4; //得到 0b00001100
//移动前先把num转换成无符号数
((uint8_t)num & 0xF0) >> 4;
- 如果是先移位再取位,移位得到
0b11111100,取位得到0b00001100,结果和预期的一致,不用关心原来num是无符号数还是有符号数。所以推荐先移位再取位。
int8_t num = 0b11000001;
(num >> 4) & 0x0F; //得到 0b00001100
示例:
ARGB颜色通过用32位二进制数来表示,从低字节到高字节依次表示B,G, R, A四个分量,求R分量的值。
(ARGB >> 16) & 0xFF;
4.4 设置某些位的值
可以通过先使用位与运算将对应位清零,再使用位或运算将对应位置位的方法来达到赋值的目的。
示例:
将16位数中的高8位赋值为0xA:
a &= ~0xFF00;
a |= (0xA << 8);
4.5 位连续翻转
取反只能将全部位同时取反,而部分位翻转可以使用异或运算。
将对应位和1做异或运算将被取反,而其它位和0异或运算不变。
示例:
连续翻转低8位:
a ^= 0xFF; //首次翻转
a ^= 0xFF; //再次翻转
...
a ^= 0xFF; //第n次翻转
4.6 lowbit应用:统计一个二进制数中为1的位数
统计为1的位数,这个可以通过不断进行消去 l o w b i t \mathrm{lowbit} lowbit 来实现,每次消去一个为1的位,只需记录变成0所需要的次数即可。
int calcNumOfBit1(unsigned int n)
{
int count = 0; //初始计数为0
//不断消去lowbit直至值为0
while (n != 0) {
n &= (n-1);
++count;
}
return count;
}
因为是计算二进制的位数,所以参数需要传入无符号整数,或者不被扩展字节的数。因为,如果被传入其它如 short, char 之类的有符号整数,如果最高位为1,扩展后高位将被全部填充1,造成计算错误。
所以在调用前,需要将参数转成同字节大小的无符号整数。
char a = 0x80; //注意,这个最高位为1的有符号整数,并且比int小
calcNumOfBit1((unsigned char)a); //转成同大小的无符号整数再调用
如果是下方的调用,那么a 由1字节的char 扩展到4字节的int(或者unsigned int),有符号数扩展后高位会被填充1,a由 0x80变成0xFFFFFF80,此时计算出错误的值。
char a = 0x80;
calcNumOfBit1(a);
4.7 lowbit应用:判断一个数是否是2的幂
如果一个数是2的幂,那么为1的二进制位只有1位,可以通过消去一个lowbit后是否为0来判断,但需要注意,0消去 l o w b i t \mathrm{lowbit} lowbit 也为0,所以需要先判断原数是否为0。
// 判断数是否是2的幂
bool isPowerOfTwo(unsigned int a)
{
return (a != 0) && ((a & (a-1)) == 0)
}
或者直接使用上面的calcNumOfBit1() 函数来计算二进制位为1的数量:
bool isPowerOfTwo(unsigned int a)
{
return calcNumOfBit1(a) == 1;
}
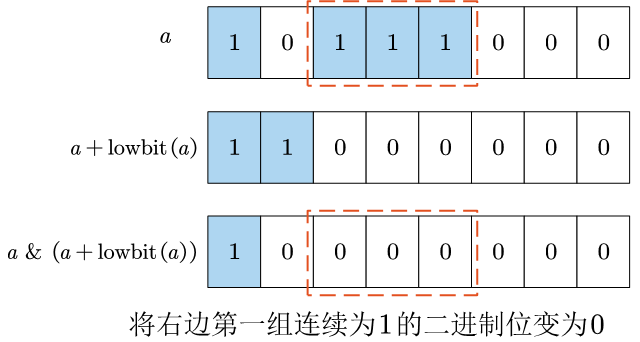
4.8 lowbit应用:将右边第一组连续为1的二进制位变为0
可以使用a & (a+lowbit(a))来消去二进制数右边连续的为1的位。
a & (a+lowbit(a)); //a & (a + (a & -a))
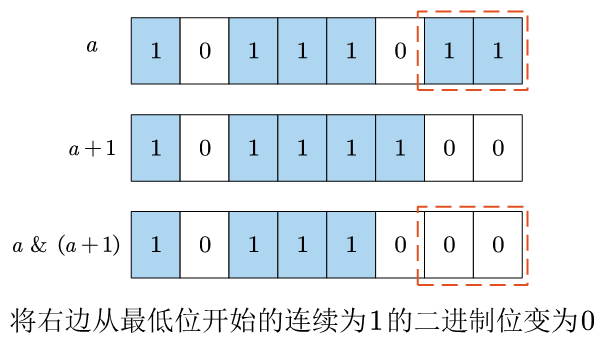
4.9 将右边从最低位开始的连续为1的二进制位变为0
a & (a + 1)
4.10 将右边从最低位开始的连续为0的二进制位变为1
a | (a-1)
同时,也可以反向操作,先将原数取反,然后去掉右边从最低位开始的连续的1,再取反回来。这两个式子其实是一致的,可以相互转换。
a = ~a; //先取反,将右边0变为1
~(a & (a + 1)); //去掉右边的1再取反回去
4.11 奇偶判断
奇数最低位为1,偶数最低位为0,因此可以用按位与运算取出二进制数的最低位,通过最低位是0还是1来判断出二进制数是奇数还是偶数。
(x & 1) == 1; //奇数判断, 或者 (x & 1) != 0
(x & 1) == 0; //偶数判断
4.12 对 2 k 2^k 2k 取模
二进制形式的数对应的十进制数值为:
a n − 1 ⋅ 2 n − 1 + ⋯ + a 2 ⋅ 2 2 + a 1 ⋅ 2 1 + a 0 ⋅ 2 0 a_{n-1} \cdot 2^{n-1} + \cdots + a_{2} \cdot 2^{2} + a_{1} \cdot 2^{1} + a_{0} \cdot 2^{0} an−1⋅2n−1+⋯+a2⋅22+a1⋅21+a0⋅20 其中, a k a_{k} ak 表示二进制形式数在第 k k k 位 ( 0 ⩽ k < n ) (0 \leqslant k < n) (0⩽k<n)上的数值(二进制位上的数值只有0和1)。
如果一个数要对 2 k 2^k 2k 取模,将其写成二进制形式后,可以发现,不低于 k k k 的位都能整除以 2 k 2^{k} 2k,余数为低 k k k 位对应的值。
因此,一个数对 2 k 2^k 2k 取模,直接取其二进制形式的低 k k k 位即可,方法是将其与低 N N N位掩码进行按位与运算:
a & ((1 << k) - 1)
当然,需要注意的是,上面的代码无法表示对 2 32 2^{32} 232取模的操作,因为 ( 1 < < 32 ) (1 << 32) (1<<32) 等于 1 而不等于 0。32位数本身就是 2 32 2^{32} 232的模,所以对 2 32 2^{32} 232取模可以做特殊处理,直接返回原值即可。
unsigned int mod2(unsigned int a, unsigned int k)
{
return (k >= 32) ? a : (a & ((1 << k) - 1));
}
上面代码中 1<< k即 2 k 2^k 2k,如果这个值已经作为 b b b 给出,那么可以写成
a & (b - 1)
当 b = 0 b=0 b=0 时,上述式子求得的值和原数相等,相当于对 2 32 2^{32} 232取模。
专栏:算法
上一篇:(二)基础运算
下一篇:(四)质数(素数)