【计算机组成 课程笔记】4.1 乘法器的硬件实现

 课程链接：

计算机组成_北京大学_中国大学MOOC(慕课)

4 - 1 - 401-乘法的运算过程（11-'33--）_哔哩哔哩_bilibili

乘法是比加减法更复杂的算数运算。小学的时候我们学习乘法，需要背一个九九乘法表。那么如果是计算机，又是如何实现乘法的呢？

1. 乘法的运算过程

我们回想一下手算乘法的过程。假设现在有两个数：2345 x 9876，首先我们要做的是最低位的乘法，5 x 6 = 30，这好像很简单，但其实这里蕴含了一个查询九九乘法表的操作。然后接着做下一步，4 x 6 = 24, + 进位3 = 27，以此类推，我们可以算出被乘数2345和乘数的最低位6的结果，14070。而这只是一个中间结果，即使是这一个中间结果，我们也进行了4次查表，4次加法运算，中间总共产生了4次进位输出。同样的中间结果我们一共有4个，最后把这4个中间结果加起来，才能得到最后的乘积。这样看来，乘法的运算实际上是非常繁琐的。

​

那么能不能不要这么繁琐？有没有比较简单的办法来解决问题？

想要找到简单的办法，我们不妨先来看一下简单的情况。我们找两个简单的数字：1000 x 1001。然后计算方法和上面是一样的，先拿乘数的最低位和被乘数的每一位相乘，得到1000，这是第一个中间结果。然后是乘数的第二位，也和被乘数的每一位相乘，从而得到了第二个中间结果0000。以此类推，得到4个中间结果，最后把这些中间结果加起来，就得到了最终的乘积。

​

对于这个例子，每个中间结果是怎么生成的呢？原则很简单，我们不用关心九九乘法表了，只用关心当前参与运算的乘数的位是不是1，如果是1，则直接将被乘数放置在与它对齐的位置上。如果是0，则直接将0放置在与它对齐的位置上。这样的运算过程就大大简化了。

但是十进制的数不可能只有0和1，上述例子对于十进制来说只是一种特殊情况。但是对于二进制来说，数字就是只有0和1，这时上面的运算方法就是通用的了。而这也正是计算机最终选择了二进制的一个重要的原因。

2. 一点历史

其实最开始的计算机也是使用十进制的，我们不妨回到二十世纪四十年代，去看两台我们非常熟悉的机器。左边这台就是ENIAC，它采用的就是十进制，右边这台是EDVAC，它采用的就是二进制。

​

ENIAC采用的是十进制，导致了它内部设计的电路非常复杂，而EDVAC采用了二进制后，就大大简化了控制逻辑。关于这一点，冯·诺依曼在他的报告中有详细的描述。

冯·诺依曼在《关于EDVAC的报告草案》中，对关于计算机应该采用什么样的进制进行了详细的分析，他主要说了这么几点：

​

关于电子计算机的更多历史，可以参看这篇博客：计算机组成_北京大学_中国大学MOOC(慕课)

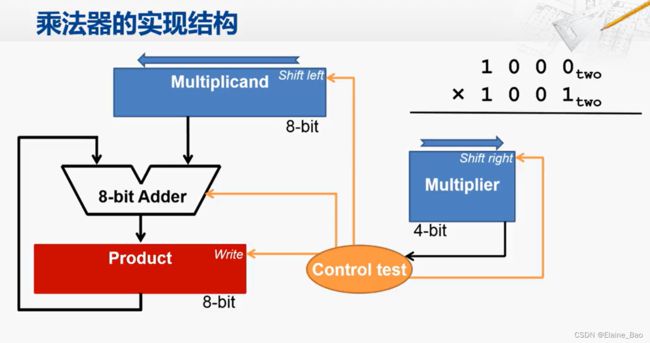
3. 乘法器的硬件实现

我们还是以刚才的那个简单的例子来展示乘法器的实现结构。1000和1001都是4-bit的数，为此我们需要一个4-bit的乘法器。

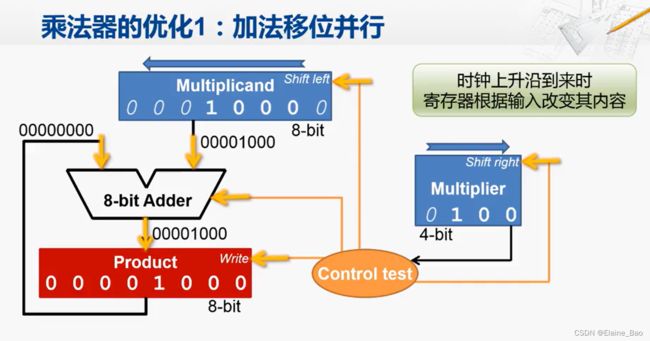
首先我们需要一个寄存器来保存被乘数（Multiplicand），这里使用8位的寄存器，而且带有左移的功能，原因是在乘法过程中被乘数需要不断左移以实现和乘数位的对齐。

另外，这个保存被乘数的寄存器有一个左移的信号输入，当外部的控制逻辑将这个信号置为有效时，在下一个时钟上升沿到来的时候，被乘数寄存器当中的内容就会向左移动一位。

第二个寄存器是乘积寄存器(Product)，这也是一个8位的寄存器，用来保存中间结果和运算的最终结果。

被乘数寄存器中的内容和乘积寄存器中的内容需要进行加法运算，这里我们需要一个8位的加法器。

另外我们还需要一个寄存器来保存乘数（Multiplier），这是一个4位的寄存器。乘数寄存器的最低位被连到了控制逻辑，控制逻辑据此来生成相关的控制信号，这些控制信号就包括是否要让加法器进行加法运算，以及是否要让乘积寄存器保存当前的计算结果，另外这个乘数寄存器还要有向右移位的功能，同样是由控制逻辑发出的控制信号来控制的。

现在我们就有了一个完整的乘法器，我们就来看一下这个乘法器是如何工作的。

​

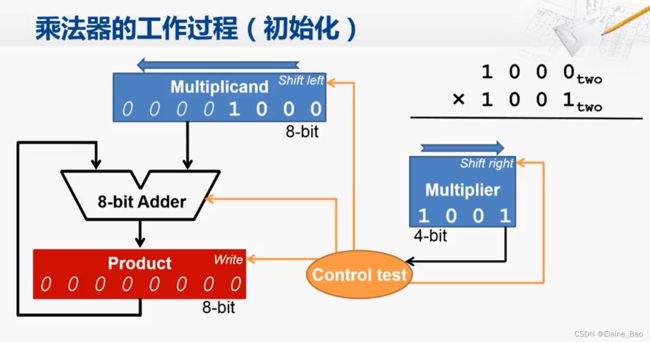
0. 初始化

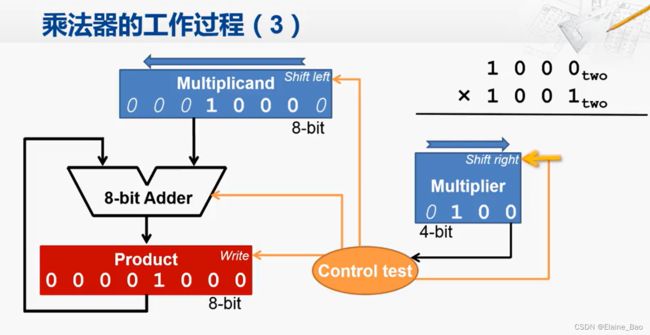
首先我们要做的是初始化，也就是对三个寄存器的内容进行设置。被乘数是1000，是1个4-bit的数，放到8-bit的寄存器中时，高4位置为0，为了便于区分，运算所得的数用粗体表示，填充的数用斜体表示。乘数寄存器很简单，4-bit的1001直接放到4-bit的寄存器中即可。然后是乘积寄存器，初始化为全0。

​

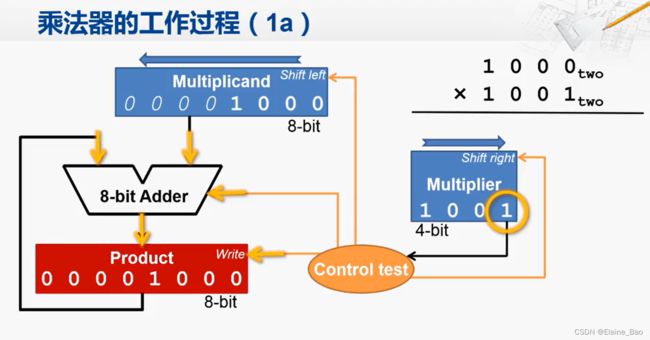
1. 加法运算

初始化结束后，就可以开始运算了。首先检查乘数寄存器的第一位，看是否为1。如果是1，则需要将被乘数寄存器中的内容和当前乘积寄存器中的内容相加。

在这一步，控制逻辑会控制加法器将两个输入进行加法运算，然后将加法器的运算结果送入乘积寄存器，在下一个时钟上升沿来临的时候，因为乘积寄存器的写入信号是有效的，所以它就会采样输入端的数据并保存到寄存器当中。这样在这个时钟上升沿之后，乘积寄存器中的内容就变成了00001000。

​

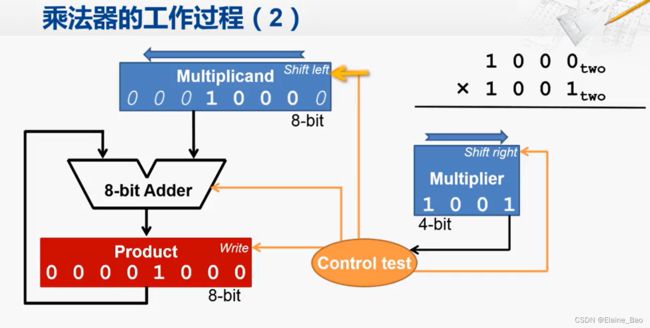
2. 对被乘数进行左移

在乘数的最低位的乘法完成后，为了为下一轮的计算做准备，我们需要对被乘数进行左移。控制逻辑会给出左移信号，在下一个时钟上升沿来临的时候，被乘数就会执行一次左移，变成00010000。

3. 对乘数进行右移

控制逻辑给出右移的控制信号到乘数寄存器，在下一个时钟上升沿来临的时候，乘数就会执行一次右移，变成0100。这样做是为了对乘数的最低位进行判断。在硬件上，如果要依次地对乘数从低位到高位进行逐位的判断，那就要用硬件来记住之前判断到了哪一位，那与其记住这样的信息，不如把乘数每次向右移一位，这样只需要每次判断乘数寄存器的最低位就可以了。而且对于乘数寄存器来说，低位使用过以后就不会再用了，所以可以丢弃。

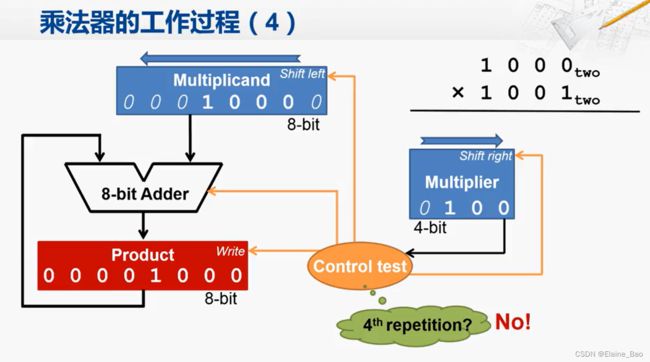
4. 判断是否进行下一轮

控制逻辑进行判断，现在是否已经完成了运算。对于4位的乘法器来说，一共要进行4次循环。简单的计数对硬件来说是很容易的，所以控制电路可以很容易地判断出当前是否已经是第4次循环了。

如果不是最后一轮循环，那么我们就要进行下一轮。第二轮的运算方式和刚才是完全一样的，重复上面的1~4步。

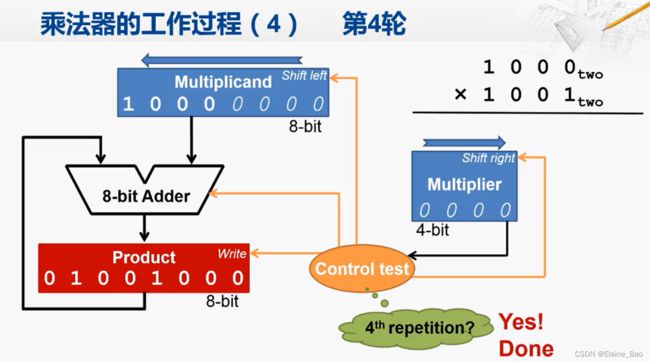
如果是最后一轮，则结束。最终结果如下所示。

5. 总结

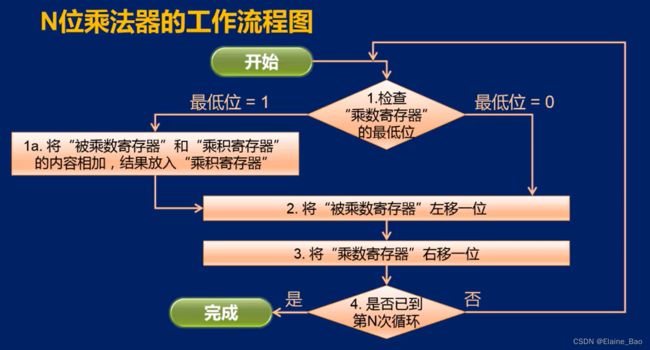
我们对上述乘法器的工作过程进行一个总结，流程图如下。

4. 乘法器的优化1

在保证乘法器功能正确性的情况下，我们再来考虑一下它的性能。

根据上面的工作流程图，我们来分析一下，进行1a步的加法，需要1个时钟周期，进行2，3步的左移，右移，各需要1个时钟周期，因此每进行1轮都需要3个时钟周期。那如果是一个32位的乘法器，则需要约100个时钟周期！我们得想一想有没有优化的办法。

首先我们很容易想到的优化，就是刚才说到的这些加法和移位的操作，能不能并行起来。是可以的。

我们知道在时钟上升沿到来之前，寄存器内容不会发生变化。因此，以当前状态为例，假设现在时钟上升沿还没有来临，那被乘数寄存器的输出就是它当前所保存的内容00001000，这8位信号会被送到加法器的输入端，而加法器的另一个输入连接的是乘积寄存器，现在的信号值是全0。而当前乘积寄存器的最低位为1，控制逻辑会据此产生相关的控制信号，让加法器进行加法运算，这样加法器就会产生对应的运算结果。与此同时，控制逻辑还会给出写的输入信号，但现在时钟上升沿还没有来，因此乘积寄存器中的值不会改变。

我们注意，这个时候，控制逻辑实际上可以同时给出被乘数寄存器和乘数寄存器的移位信号，这样现在控制逻辑就将刚才流程图上的第1a,2,3步的控制信号都置为有效了，但因为时钟上升沿还没有来，所以这些寄存器的内容都不会发生变化。

当时钟上升沿到来的时候，这些寄存器就会根据输入改变其内容。这样我们就在同一个时刻完成了加法和移位的操作。

经过上述优化后，工作流程变成了下图这样。这样每次循环只需要1个时钟周期，性能为又花钱的三倍。

5. 乘法器的优化2

当我们购买一台计算机时，不仅希望它的性能足够好，还希望它的价格足够低。那对于CPU这样的集成电路芯片来说，它的价格的一个重要因素就是其中晶体管的数量，或者说是芯片的面积。因此在我们设计各个功能部件的时候，如何减小芯片的面积，也是一个重要的优化方向。所以对于乘法器的优化，我们也来考虑一下有哪些不必要的硬件资源可以被省略。

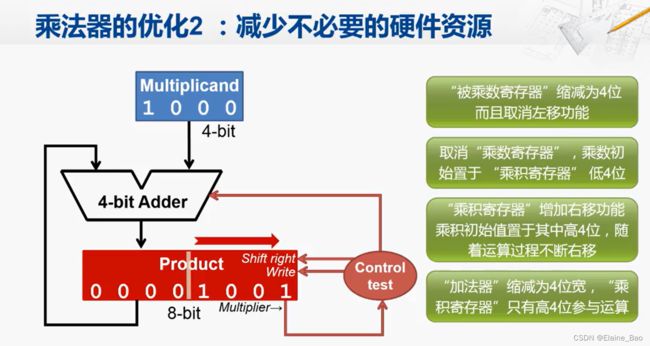
首先我们来看被乘数寄存器，它是一个8-bit的寄存器，但实际其中的有效数字始终只有4位。那我们可能会说这是为了进行移位啊，移位是为了和乘积的中间结果进行对齐，然后进行运算，这就是这个乘法运算的要点之一啊。其实这是我们当时为了实现的简便所做出的选择。我们先不管这些，在这里用一个8位的寄存器来保存一个4位的数，这显然就是浪费了。

再来看一下乘数寄存器，乘数寄存器是4-bit的，看起来没有浪费。但是仔细想一想，这个寄存器里的有效数字每个周期都会减少1位，所以在运算的过程中，这个寄存器逐渐就出现了浪费的问题。

再来看一下乘积寄存器，最终的乘积确实需要8-bit来保存，但是问题在于，这个寄存器初始时有效数字只有4位，高4位是浪费的，而随着每个周期的运算，乘积寄存器的有效位数每周期会增加1位。

最后说到加法器，实际上每次参与运算的有效数字只有4位，因此并不需要8位的加法器。

好，现在我们就找到了4个浪费的点，那我们就来看一下如何优化。

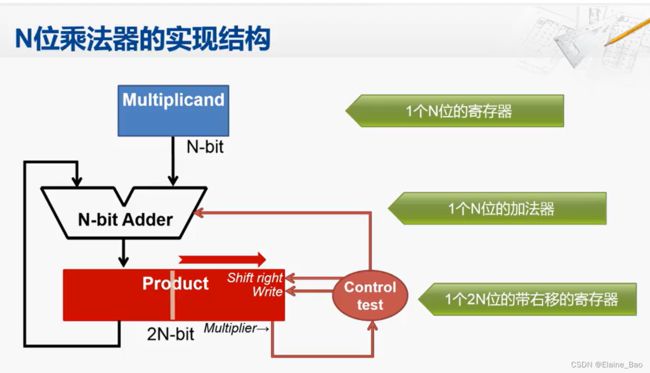
然后，将上述的优化推广到N位乘法器，我们就得到了如下的结构：