机器学习笔记之最优化理论与方法(三)凸集的简单认识(下)
机器学习笔记之最优化理论与方法——凸集的简单认识[下]
- 引言
-
- 回顾:基本定义——凸集
- 关于保持集合凸性的运算
-
- 仿射变换
- 凸集基本性质:投影定理
- 点与凸集的分离
- 支撑超平面定理
引言
继续凸集的简单认识(上)进行介绍,本节将介绍凸集的基本性质以及相关定理。
回顾:基本定义——凸集
关于凸集 ( Convex Set ) (\text{Convex Set}) (Convex Set)的定义可简单表述为:可行域 C \mathcal C C中任意两点间的连线,其连线上的任意一点仍在可行域 C \mathcal C C范围内。对应数学符号表示如下:
∀ x , y ∈ C ; ∀ λ ∈ [ 0 , 1 ] ⇒ λ ⋅ x + ( 1 − λ ) ⋅ y ∈ C \forall x,y \in \mathcal C;\forall \lambda \in [0,1] \Rightarrow \lambda \cdot x + (1 - \lambda) \cdot y \in \mathcal C ∀x,y∈C;∀λ∈[0,1]⇒λ⋅x+(1−λ)⋅y∈C
如果记线性规划: min { c T x ∣ A x = b , x ≥ 0 } \min \{c^T x \mid \mathcal A x = b,x \geq 0\} min{cTx∣Ax=b,x≥0}的最优解组成的集合为 S \mathcal S S,那么 S \mathcal S S是否为凸集 ? ? ?
自然是凸集:
- 从最优解集合 S \mathcal S S中任取两点 x 1 , x 2 ∈ S x_1,x_2 \in \mathcal S x1,x2∈S,必然有:
其中这里v ∗ v^* v∗记作可行域范围内,使c T x c^Tx cTx达到最小的最优解。
c T x 1 = c T x 2 = v ∗ c^Tx_1 = c^Tx_2 = v^* cTx1=cTx2=v∗ - 根据凸集定义, ∀ λ ∈ [ 0 , 1 ] \forall \lambda \in [0,1] ∀λ∈[0,1],观察 λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 \lambda \cdot x_1 + (1 - \lambda) \cdot x_2 λ⋅x1+(1−λ)⋅x2是否也在最优解集合 S \mathcal S S内即可。将该点代入有:
c T [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] = λ ⋅ c T x 1 ⏟ v ∗ + ( 1 − λ ) ⋅ c T x 2 ⏟ v ∗ = v ∗ \begin{aligned} & \quad c^T[\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] \\ & = \lambda \cdot \underbrace{c^Tx_1}_{v^*} + (1 - \lambda) \cdot \underbrace{c^Tx_2}_{v^*} \\ & = v^* \end{aligned} cT[λ⋅x1+(1−λ)⋅x2]=λ⋅v∗ cTx1+(1−λ)⋅v∗ cTx2=v∗
可以看出: c T [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] c^T[\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] cT[λ⋅x1+(1−λ)⋅x2]依然是最优解。也就是说:点 λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ∈ S \lambda \cdot x_1 + (1 - \lambda) \cdot x_2 \in \mathcal S λ⋅x1+(1−λ)⋅x2∈S。 S \mathcal S S是凸集得证。
关于保持集合凸性的运算
所谓保持集合凸性的运算,即凸集执行一系列运算后,其结果是凸集的性质不发生变化。
设 C 1 , C 2 ∈ R n \mathcal C_1,\mathcal C_2 \in \mathbb R^n C1,C2∈Rn,并且是凸集。则有:
- 交集 C 1 ∩ C 2 = { x ∣ x ∈ C 1 , x ∈ C 2 } \mathcal C_1 \cap \mathcal C_2 = \{x \mid x \in \mathcal C_1,x \in \mathcal C_2\} C1∩C2={x∣x∈C1,x∈C2}同样是凸集;
相反,并集 C 1 ∪ C 2 \mathcal C_1 \cup \mathcal C_2 C1∪C2未必是凸集~ - 关于集合的加减运算: C 1 ± C 2 = { x ± y ∣ x ∈ C 1 , y ∈ C 2 } \mathcal C_1 \pm \mathcal C_2 = \{x \pm y \mid x \in \mathcal C_1,y \in \mathcal C_2\} C1±C2={x±y∣x∈C1,y∈C2}同样是凸集。
如果存在一个由 n n n维向量组成的集合 S \mathcal S S:
{ S = { x ∈ R n ∣ ∣ P ( t ) ∣ ≤ 1 , ∣ t ∣ ≤ π 3 } P ( t ) = ∑ i = 1 n x i ⋅ cos ( i ⋅ t ) \begin{cases} \begin{aligned} & \mathcal S = \left\{x \in \mathbb R^n \mid |\mathcal P(t)| \leq 1, |t| \leq \frac{\pi}{3} \right\} \\ & \mathcal P(t) = \sum_{i=1}^n x_i \cdot \cos (i \cdot t) \end{aligned} \end{cases} ⎩ ⎨ ⎧S={x∈Rn∣∣P(t)∣≤1,∣t∣≤3π}P(t)=i=1∑nxi⋅cos(i⋅t)
那么集合 S \mathcal S S是否为凸集 ? ? ?
- 首先,由于 S \mathcal S S是关于 x x x的集合,因而 P ( t ) \mathcal P(t) P(t)可看作是一个关于 x x x的线性表达式。并且有:
− 1 ≤ ∑ i = 1 n x i ⋅ cos ( i ⋅ t ) ≤ 1 -1 \leq \sum_{i=1}^n x_i \cdot \cos (i \cdot t) \leq 1 −1≤i=1∑nxi⋅cos(i⋅t)≤1 - 如果 t t t给定,那么可以将上式视作: { ∑ i = 1 n x i ⋅ cos ( i ⋅ t ) ≤ 1 ∑ i = 1 n x i ⋅ cos ( i ⋅ t ) ≥ − 1 \begin{cases} \sum_{i=1}^n x_i \cdot \cos(i \cdot t) \leq 1 \\ \sum_{i=1}^n x_i \cdot \cos(i \cdot t) \geq -1 \\ \end{cases} {∑i=1nxi⋅cos(i⋅t)≤1∑i=1nxi⋅cos(i⋅t)≥−1所描述的一对半空间的交集。
- 由于 − π 3 ≤ t ≤ π 3 \begin{aligned}-\frac{\pi}{3}\leq t \leq \frac{\pi}{3}\end{aligned} −3π≤t≤3π,是一个连续的范围,那么:可以在该范围内取出无穷个 t t t,从而得到无穷对半空间的交集。而半空间自身是凸集,那么无穷对半空间的交集同样是凸集。因而 S \mathcal S S是凸集。
准确的说,S \mathcal S S是一个多面体。
如果 n = 2 n = 2 n=2,此时仅包含两个变量 x 1 , x 2 x_1,x_2 x1,x2。可以通过 2 2 2维图像的方式观察这个多面体凸集描述的范围。具体代码如下:
在 t t t固定的情况下,函数 ∣ P ( t ) ∣ = 1 ⇒ P ( t ) = ± 1 |\mathcal P(t)| = 1 \Rightarrow \mathcal P(t) = \pm1 ∣P(t)∣=1⇒P(t)=±1可看做是 ϕ ( x 1 , x 2 ) \phi(x_1,x_2) ϕ(x1,x2)的表示。令 ϕ ( x 1 , x 2 ) = P ( t ) ∓ 1 ≜ 0 \phi(x_1,x_2) = \mathcal P(t) \mp 1 \triangleq 0 ϕ(x1,x2)=P(t)∓1≜0,从而得到 x 1 , x 2 x_1,x_2 x1,x2之间的函数关系:
x 1 ⋅ cos t + x 2 ⋅ cos ( 2 ⋅ t ) = ± 1 ⇒ x 1 = ± 1 − x 2 ⋅ cos ( 2 ⋅ t ) cos t \begin{aligned} & \quad x_1 \cdot \cos t + x_2 \cdot \cos (2 \cdot t) = \pm1 \\ & \Rightarrow x_1 = \pm\frac{1 - x_2 \cdot \cos (2 \cdot t)}{\cos t} \end{aligned} x1⋅cost+x2⋅cos(2⋅t)=±1⇒x1=±cost1−x2⋅cos(2⋅t)
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.linspace(-2.5,2,100)
tChoice = np.linspace(-1 * (math.pi / 3),math.pi / 3,30)
def phi(x1,t):
return (1 - x1 * math.cos(2 * t)) / math.cos(t)
def phiTrans(x1,t):
return (x1 * math.cos(2 * t) - 1) / math.cos(t)
for t in tChoice:
y = list()
y2 = list()
for x1 in x:
y.append(phi(x1,t))
y2.append(phiTrans(x1,t))
plt.plot(x,y,c="tab:red")
plt.plot(x,y2,c="tab:red")
plt.show()
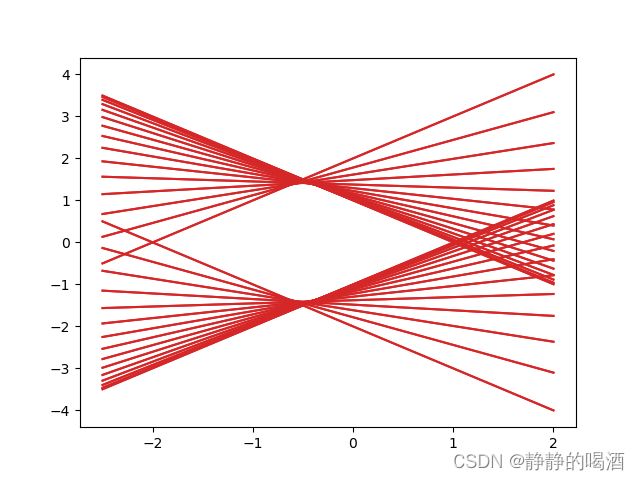
对应图像结果表示如下:
中间围成的区域就是 n = 2 n=2 n=2条件下的多面体凸集 S \mathcal S S。
仿射变换
仿射变换 ( Affine Transformation ) (\text{Affine Transformation}) (Affine Transformation)同样是保持集合凸性的一种运算。具体描述如下:
需要注意的是:线性变换是特殊的仿射变换。
假设函数 f ( ⋅ ) : R n ↦ R m f(\cdot):\mathbb R^n \mapsto \mathbb R^m f(⋅):Rn↦Rm是仿射函数,即 f ( x ) = A x + b f(x) = \mathcal Ax + b f(x)=Ax+b。其中 A ∈ R m × n , b ∈ R m \mathcal A \in \mathbb R^{m \times n},b \in \mathbb R^{m} A∈Rm×n,b∈Rm,则有如下结论:
其中 f − 1 ( ⋅ ) f^{-1}(\cdot) f−1(⋅)表示仿射函数 f ( ⋅ ) f(\cdot) f(⋅)的逆。
- 如果 C \mathcal C C是凸集 ⇒ f ( C ) = { f ( x ) ∣ x ∈ C } \Rightarrow f(\mathcal C) = \{f(x) \mid x \in \mathcal C\} ⇒f(C)={f(x)∣x∈C}也是凸集;
- 如果 C \mathcal C C是凸集 ⇒ f − 1 ( C ) = { x ∣ f ( x ) ∈ C } \Rightarrow f^{-1}(\mathcal C) = \{x \mid f(x) \in \mathcal C\} ⇒f−1(C)={x∣f(x)∈C}也是凸集;
以第一项为例:对于 ∀ y 1 , y 2 ∈ f ( C ) \forall y_1,y_2 \in f(\mathcal C) ∀y1,y2∈f(C),必然有:
{ y 1 = A x 1 + b y 2 = A x 2 + b x 1 , x 2 ∈ C \begin{cases} y_1 = \mathcal Ax_1 + b \\ y_2 = \mathcal Ax_2 + b \end{cases}\quad x_1,x_2 \in \mathcal C {y1=Ax1+by2=Ax2+bx1,x2∈C
根据凸集的定义,对 ∀ λ ∈ [ 0 , 1 ] \forall \lambda \in [0,1] ∀λ∈[0,1],将 λ ⋅ y 1 + ( 1 − λ ) ⋅ y 2 \lambda \cdot y_1 + (1 - \lambda) \cdot y_2 λ⋅y1+(1−λ)⋅y2展开,有:
λ ⋅ y 1 + ( 1 − λ ) ⋅ y 2 = λ ( A x 1 + b ) + ( 1 − λ ) ⋅ ( A x 2 + b ) = A [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] + b \begin{aligned} \lambda \cdot y_1 + (1 - \lambda) \cdot y_2 & = \lambda (\mathcal Ax_1 + b) + (1 - \lambda) \cdot(\mathcal Ax_2 + b) \\ & = \mathcal A [\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] + b \end{aligned} λ⋅y1+(1−λ)⋅y2=λ(Ax1+b)+(1−λ)⋅(Ax2+b)=A[λ⋅x1+(1−λ)⋅x2]+b
由于 x 1 , x 2 ∈ C x_1,x_2 \in \mathcal C x1,x2∈C,且 C \mathcal C C是凸集,必然有:
∀ λ ∈ [ 0 , 1 ] ⇒ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ∈ C \forall \lambda \in [0,1] \Rightarrow \lambda \cdot x_1 + (1 - \lambda) \cdot x_2 \in \mathcal C ∀λ∈[0,1]⇒λ⋅x1+(1−λ)⋅x2∈C
从而有:
λ ⋅ y 1 + ( 1 − λ ) ⋅ y 2 ∈ f ( C ) \lambda \cdot y_1 + (1 - \lambda) \cdot y_2 \in f(\mathcal C) λ⋅y1+(1−λ)⋅y2∈f(C)
因而 f ( C ) f(\mathcal C) f(C)也是凸集。
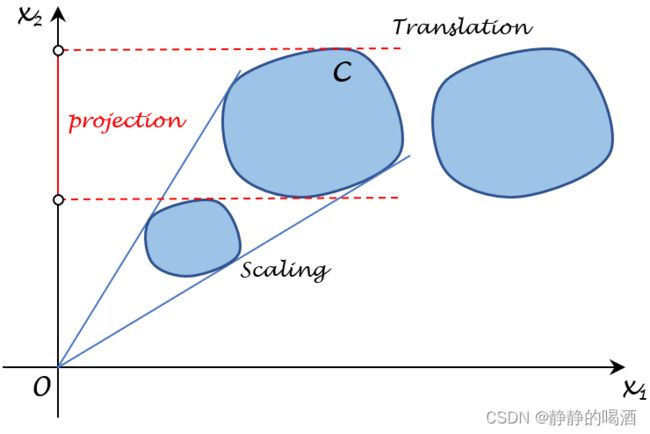
一些特殊的仿射变换有:
其中 α , β \alpha,\beta α,β是常数。
- 放缩 ( Scaling ) (\text{Scaling}) (Scaling):
α ⋅ C = { α ⋅ x ∣ x ∈ C } \alpha \cdot \mathcal C = \{\alpha \cdot x \mid x \in \mathcal C\} α⋅C={α⋅x∣x∈C} - 平移 ( Translation ) (\text{Translation}) (Translation):
β + C = { β + x ∣ x ∈ C } \beta+ \mathcal C = \{\beta+ x \mid x \in \mathcal C\} β+C={β+x∣x∈C} - 投影 ( Projection ) (\text{Projection}) (Projection)
{ x 1 ∣ ( x 1 x 2 ) ∈ C } \left\{x^1 \mid \begin{pmatrix}x^1 \\ x^2\end{pmatrix} \in \mathcal C\right\} {x1∣(x1x2)∈C}
凸集基本性质:投影定理
投影定理描述如下:
假设 C ⊂ R n \mathcal C \subset \mathbb R^n C⊂Rn,是一个非空闭凸集; y ∈ R n y \in \mathbb R^n y∈Rn但 y ∉ C y \notin \mathcal C y∈/C,有:
- 存在唯一的点 x ˉ ∈ C \bar{x} \in \mathcal C xˉ∈C,使得 x ˉ \bar{x} xˉ是 y y y到 C \mathcal C C的距离最小的点,且有:
距离最小的点即投影点。
∥ x ˉ − y ∥ = inf { ∥ x − y ∥ ∣ x ∈ C } > 0 \|\bar {x} - y\| = \inf\{\|x - y\| \mid x \in \mathcal C\} > 0 ∥xˉ−y∥=inf{∥x−y∥∣x∈C}>0 - x ˉ \bar{x} xˉ是 y y y到 C \mathcal C C的最小距离点的充要条件是:
( x − x ˉ ) T ( x ˉ − y ) ≤ 0 ∀ x ∈ C (x - \bar{x})^T (\bar{x} - y) \leq 0 \quad \forall x \in \mathcal C (x−xˉ)T(xˉ−y)≤0∀x∈C
证明过程:
-
存在性:
关于 y y y到 C \mathcal C C的距离,本质上是描述 y y y与凸集 C \mathcal C C中点的距离,假设 x ′ ∈ C x' \in \mathcal C x′∈C,对应目标函数表示如下:
这里使用二范数表示x ′ x' x′与y y y之间的距离。
min f ( x ) = ∥ y − x ′ ∥ 2 2 \min f(x) = \|y - x'\|_2^2 minf(x)=∥y−x′∥22
但我们要找的是距离最小的点,而这个 x ′ x' x′可能并不是那个点。因而我们要找的距离最小点的可行域表示为:
s.t. x ∈ C ∩ N d ( y ) \text{s.t. } x \in \mathcal C \cap \mathcal N_d(y) s.t. x∈C∩Nd(y)
其中 d = ∣ ∣ y − x ′ ∣ ∣ 2 2 d = ||y - x'||_2^2 d=∣∣y−x′∣∣22;而 N d ( y ) \mathcal N_d(y) Nd(y)表示以 y y y为圆心,半径为 d d d的圆所描述的范围。也就是说:如果 x ′ x' x′不是距离最小点,并不需要重新从范围 C \mathcal C C中寻找点,只需要在交集内寻找距离最小点即可。对应图像表示如下:
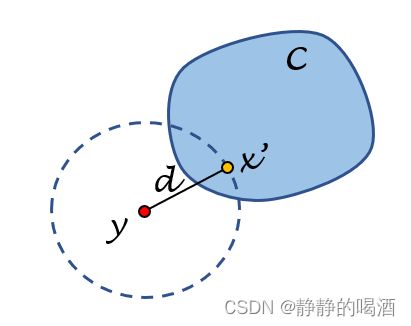
由于 C \mathcal C C是非空闭凸集,说明这个交集有界。在连续函数(距离函数)在有界空间内求最小值,那么该值必然可达。 -
唯一性(反证):
对应图像表示如下~

不妨设 x ′ , x ˉ ( x ˉ ≠ x ′ ) x',\bar{x}(\bar x \neq x') x′,xˉ(xˉ=x′)均是投影点,从而有:
d = ∥ y − x ˉ ∥ 2 2 = ∥ y − x ′ ∥ 2 2 d = \|y - \bar{x}\|_2^2 = \|y - x'\|_2^2 d=∥y−xˉ∥22=∥y−x′∥22
由于 x ˉ ≠ x ′ \bar{x} \neq x' xˉ=x′,连接两点,根据凸集合的定义:两点连线上的点必然也 ∈ C \in \mathcal C ∈C。此时, x ′ , x ˉ , y x',\bar{x},y x′,xˉ,y三个点构成一个等腰三角形,从而有:线段 x ˉ x ′ \bar{x}x' xˉx′上的点到 y y y的距离必然小于 d d d。从而得出: x ˉ , x ′ \bar{x},x' xˉ,x′不是投影点,这与假设冲突。因而 x ′ , x ˉ x',\bar{x} x′,xˉ两点重合,投影点具有唯一性。 -
充要条件:观察下面图像:
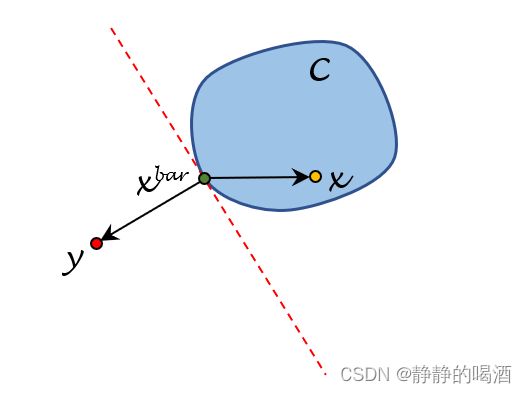
假设此时已经找到了投影点 x ˉ \bar{x} xˉ,必然有:- 向量 y − x ˉ y - \bar{x} y−xˉ与 x ˉ \bar{x} xˉ在凸集 C \mathcal C C的切线垂直;
- 并且凸集 C \mathcal C C中除去 x ˉ \bar{x} xˉ之外的其他点均与 y − x ˉ y - \bar{x} y−xˉ处在由切线划分的不同的半空间。
从而有:向量 y − x ˉ y - \bar{x} y−xˉ与 x − x ˉ ( ∀ x ∈ C ) x - \bar{x}(\forall x \in \mathcal C) x−xˉ(∀x∈C)之间的夹角总是大于等于 9 0 。 90^。 90。。即:
等于9 0 。 90^。 90。即x , x ˉ x,\bar{x} x,xˉ重合~
( y − x ˉ ) T ( x − x ˉ ) = ∥ y − x ˉ ∥ ⋅ ∥ x − x ˉ ∥ cos θ ≤ 0 (y - \bar{x})^T (x - \bar{x}) = \|y - \bar{x}\| \cdot \|x - \bar{x}\| \cos \theta \leq 0 (y−xˉ)T(x−xˉ)=∥y−xˉ∥⋅∥x−xˉ∥cosθ≤0
反之同理。
点与凸集的分离
定理描述如下:
假设 C 1 , C 2 \mathcal C_1,\mathcal C_2 C1,C2是两个非空凸集,若存在非零 α ∈ R n \alpha \in \mathbb R^n α∈Rn和 b ∈ R b \in \mathbb R b∈R使得:
或者写作: α T z ≤ α T x ∀ x ∈ C 1 , ∀ z ∈ C 2 \alpha^T z \leq \alpha^Tx \quad \forall x \in \mathcal C_1,\forall z \in \mathcal C_2 αTz≤αTx∀x∈C1,∀z∈C2
{ α T x ≥ b ∀ x ∈ C 1 α T z ≤ b ∀ z ∈ C 2 \begin{cases} \alpha^T x \geq b \quad \forall x \in \mathcal C_1 \\ \alpha^T z \leq b \quad \forall z \in \mathcal C_2 \end{cases} {αTx≥b∀x∈C1αTz≤b∀z∈C2
则称超平面 H = { x ∣ α T x = b } \mathcal H = \{x \mid \alpha^T x = b\} H={x∣αTx=b}分离集合 C 1 , C 2 \mathcal C_1,\mathcal C_2 C1,C2。
严格分离:
观察上述的分离定义,由于超平面可以取等,使得凸集 C 1 , C 2 \mathcal C_1,\mathcal C_2 C1,C2与超平面 H \mathcal H H之间可能存在交集。而严格分离定义在上述分离定义的基础上, C 1 , C 2 \mathcal C_1,\mathcal C_2 C1,C2均不与超平面 H \mathcal H H之间存在交集。即:
{ α T x > b ∀ x ∈ C 1 α T z < b ∀ z ∈ C 2 \begin{cases} \alpha^T x > b \quad \forall x \in \mathcal C_1 \\ \alpha^T z < b \quad \forall z \in \mathcal C_2 \end{cases} {αTx>b∀x∈C1αTz<b∀z∈C2
基于上述定义,从而有如下推论:
- 两个不相交的非空凸集,它们一定能分离;
相反,如果存在集合不是凸集,那就不一定了~ - 假设 C ⊂ R n \mathcal C \subset \mathbb R^n C⊂Rn是非空闭凸集,点 y ∉ C y \notin \mathcal C y∈/C,必然存在超平面 H \mathcal H H将 y y y与 C \mathcal C C分离。
例如上面描述投影定理充要条件中的红色虚线。实际上:垂直于 y − x ˉ y - \bar{x} y−xˉ并且经过线段 x ˉ y \bar{x}y xˉy上的超平面都是满足要求的。
{ α = y − x ˉ α T ( y − x ) ≥ 0 ⇒ α T y ≥ α T x ∀ x ∈ C \begin{cases} \alpha = y - \bar{x} \\ \alpha^T(y - x) \geq 0 \Rightarrow \alpha^Ty \geq \alpha^T x \quad \forall x \in \mathcal C \end{cases} {α=y−xˉαT(y−x)≥0⇒αTy≥αTx∀x∈C
上面式子描述的向量 y − x y-x y−x描述的是从凸集 C \mathcal C C中的任意一点指向 y y y的向量,而该向量和向量 y − x ˉ y - \bar{x} y−xˉ之间的夹角必然是锐角。
支撑超平面定理
定理描述如下:
假设 C ∈ R n \mathcal C \in \mathbb R^n C∈Rn是非空闭凸集,其中 x ˉ \bar{x} xˉ是 C \mathcal C C的边界点: x ˉ ∈ ∂ C \bar{x} \in \partial \mathcal C xˉ∈∂C,则存在非零向量 α ∈ R n \alpha \in \mathbb R^n α∈Rn使得:
其中 ∂ C \partial \mathcal C ∂C表示集合 C \mathcal C C的边界点; int C \text{int} \mathcal C intC表示集合 C \mathcal C C不包含边界点的所有内点; c l C cl\mathcal C clC表示由内点、边界点构成的集合(闭包) ⇒ \Rightarrow ⇒非空的闭凸集合。
α T x ≤ α T x ˉ ∀ x ∈ c l C \alpha^T x \leq \alpha^T \bar{x} \quad \forall x \in \mathcal clC αTx≤αTxˉ∀x∈clC
此时,也称超平面 H = { x ∈ R n ∣ α T x = α T x ˉ } \mathcal H = \{x \in \mathbb R^n \mid \alpha^T x = \alpha^T \bar{x}\} H={x∈Rn∣αTx=αTxˉ}是凸集 C \mathcal C C在 x ˉ \bar{x} xˉ处的支撑超平面。对应图像表示如下:

证明过程:
已知 x ˉ ∈ ∂ C \bar{x} \in \partial \mathcal C xˉ∈∂C,要证: ∃ α ≠ 0 \exist \alpha \neq 0 ∃α=0使得 α T x ≤ α T x ˉ ∀ x ∈ c l C \alpha^T x \leq \alpha^T \bar{x} \quad \forall x \in cl\mathcal C αTx≤αTxˉ∀x∈clC
由于 x ˉ ∈ ∂ C \bar{x} \in \partial \mathcal C xˉ∈∂C,则必然可以找到收敛于 x ˉ \bar{x} xˉ的点序列 { x k } ↦ x ˉ \{x_k\} \mapsto \bar{x} {xk}↦xˉ并且 { x k } ∉ c l C \{x_k\} \notin cl\mathcal C {xk}∈/clC
也就是说:这个点序列 { x k } \{x_k\} {xk}并不是从凸集 C \mathcal C C内找的,而是从集合之外找的。
由于 x k ∉ c l C x_k \notin cl\mathcal C xk∈/clC,根据分离定理,存在超平面/非零法向量 α k \alpha_k αk,有:
也就是说:每一次迭代,总会找到相应的超平面 α k \alpha_k αk将 C \mathcal C C与 x k x_k xk做分离。
α k T x ≤ α k T x k x ∈ c l C \alpha_k^T x \leq \alpha_k^T x_k \quad x \in cl\mathcal C αkTx≤αkTxkx∈clC
由于 α k \alpha_k αk是法向量,我们更关注它的方向性而不是大小。因而不妨设 ∥ α k ∥ = 1 \|\alpha_k\| = 1 ∥αk∥=1,则有:法向量序列 { α k } \{\alpha_k\} {αk}随着 { x k } \{x_k\} {xk}的迭代过程收敛到某位置。当 k ⇒ ∞ k \Rightarrow \infty k⇒∞时,有:
α T x ˉ = lim k ⇒ ∞ α k T ⋅ x k ≥ α T x x ∈ c l C \alpha^T \bar{x} = \mathop{\lim}\limits_{k \Rightarrow \infty} \alpha_k^T \cdot x_k \geq \alpha^T x \quad x \in cl\mathcal C αTxˉ=k⇒∞limαkT⋅xk≥αTxx∈clC
证毕。使用图像表示如下:

相关参考:
最优化理论与方法-第二讲-凸集