【LeetCode-中等题】200. 岛屿数量
文章目录
-
- 题目
- 方法一:深度优先搜索 dfs
- 方法二:广度优先搜索 bfs
- 方法三:(重点掌握)并查集
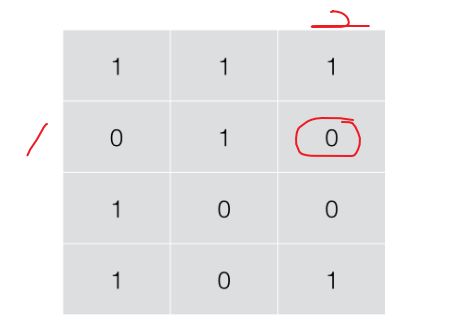
题目
方法一:深度优先搜索 dfs
思路:让一个扫描指针扫描每一个格子,然后每扫到一个为1的格子,道与数量count+1,,并且对这个格子进行dfs(四个方向dfs)将此次格子的dfs周边的格子全部置为0,接着指针继续扫描下一个为1的格子,重复上面的动作。
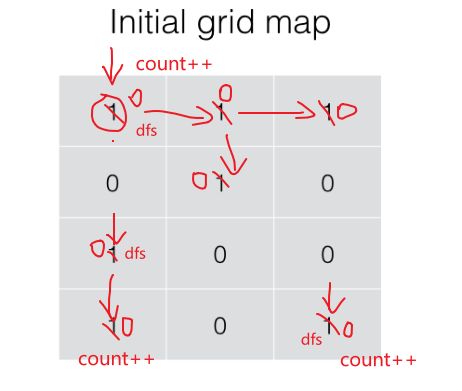
扫描整个二维网格。如果一个位置为 1,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。
最终岛屿的数量就是我们进行深度优先搜索的次数。
图的dfs遍历框架思路:岛屿类问题的通用解法、DFS 遍历框架
//方法一 深度优先搜索 dfs
int row = 0; //网格行数 全局变量
int col = 0; //网格列数 全局变量
public int numIslands(char[][] grid) {
if(grid[0].length==0) return 0;
this.row = grid.length;//给行列全局变量赋值
this.col = grid[0].length;
int count = 0;//岛屿计数
for(int r = 0;r<row ;r++)//遍历网格每一个各格子
for(int c = 0;c<col ;c++){
if(grid[r][c]=='1'){//如果网格数字为1,说明存在岛屿
count++;
dfs(grid,r,c);//对该格子进行dfs 将这个格子旁边的1统统置为0
}
}
return count;
}
// dfs
public void dfs(char[][] grid ,int r,int c){
if(r>=row || c>=col || r<0 || c<0 || grid[r][c]=='0'){ //递归终止条件
return;
}
grid[r][c] ='0';// 将1全部置为0
//对四个方向进行递归
dfs(grid,r-1,c);
dfs(grid,r+1,c);
dfs(grid,r,c+1);
dfs(grid,r,c-1);
}
方法二:广度优先搜索 bfs
思路:
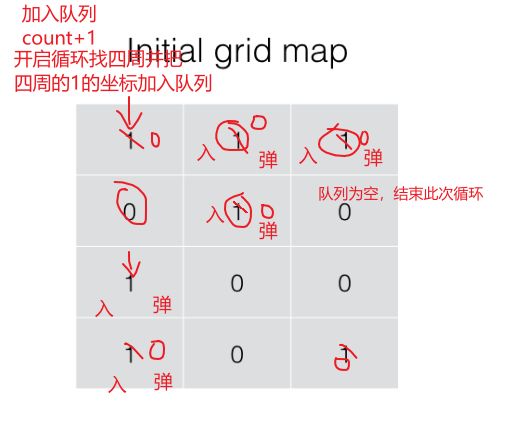
当遍历指针指向了一个1的网格,count++,就率先将该位置的绝对坐标(行*总列数+列)存入队列中,然后将该位置设置为0,接着进行while循环,从队列取出绝对位置,转换为x y坐标,然后根据x y 坐标 去判断当前位置的上下左右是否有1,是的话,就加入队列,并且置为0,直到循环结束(while循环做的事,就是在判断从对列拿出的位置周围四个方向是否有1,有就全部置为0,持续处理队列弹出的元素)
然后继续移动指针到下一个1的位置,继续前面的步骤
因为队列只能存一个整数,所以只能先存绝对位置,到时候弹出这个绝对位置的值,转换为行列就可以了
绝对位置:(举例 1,2 位置)
绝对位置 = 1*列数(3)+2 = 5
解析绝对位置:
行: 5 /列数 (3)= 1
列: 5%列数(3)= 2
扫描整个二维网格。如果一个位置为 1,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。
最终岛屿的数量就是我们进行深度优先搜索的次数。
// 方法二 广度优先搜索 bfs
int row = 0; //网格行数 全局变量
int col = 0; //网格列数 全局变量
public int numIslands(char[][] grid) {
if(grid == null||grid[0].length==0) return 0;
this.row = grid.length;//给行列全局变量赋值
this.col = grid[0].length;
int count = 0;
Queue<Integer> queue = new LinkedList<>();
for(int r = 0 ; r<row ; r++)
for(int c = 0 ; c<col ; c++){
if(grid[r][c]=='1'){// 说明有岛屿
count++;
//将当前位置的x和y坐标入队 直接存入整数绝对位置
queue.offer(r*col+c); //第r行 第c列
grid[r][c]='0';//然后置为0
while(!queue.isEmpty()){//如果队列不为空 说明其中有包含1 的元素
int mid = queue.poll(); //取出该元素的绝对坐标
//将该元素绝对坐标转换为 对应的x 和 y坐标
int x = mid / col;//行
int y = mid % col;//列
//对该元素四个方向判断是否有1,是就将对应绝对坐标加入到队列,并且将该位置置为0
//上
if(y-1 >=0 && grid[x][y-1]=='1'){
queue.offer(x*col +y-1);
grid[x][y-1]='0';
}
//下
if(y+1 < col && grid[x][y+1]=='1'){
queue.offer(x*col +y+1);
grid[x][y+1]='0';
}
//左
if(x-1 >=0 && grid[x-1][y]=='1'){
queue.offer((x-1)*col +y);
grid[x-1][y]='0';
}
//右
if(x+1 <row && grid[x+1][y]=='1'){
queue.offer((x+1)*col +y);
grid[x+1][y]='0';
}
}
}
}
return count;
}
方法三:(重点掌握)并查集
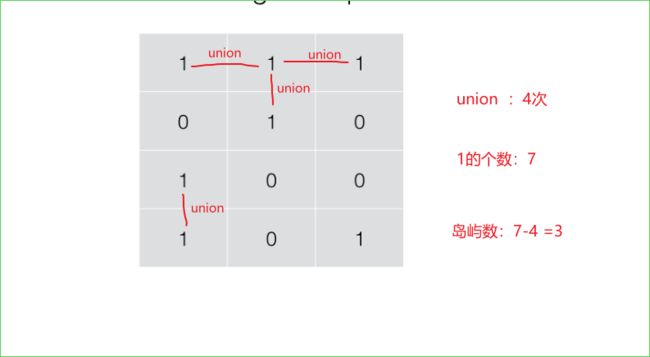
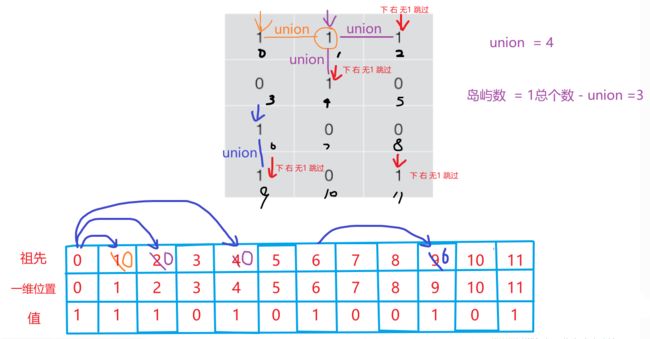
方法三 并查集 关键在于find方法找祖先 然后union方法同化不是相同祖先的两个临近格子(只需要比较下 和右两个方向) 以及将二维数组,以行坐标*列数+列坐标 = 祖先 的方式转为一维数组 方便进行找祖先 同化祖先,
岛屿数 = 1的个数-同化次数
这题的对比方向可以只是 往右和往下对比就足够了,无需往上,往左 (往上往左都是重复动作)
int[] p = null;//祖先数组 初始化 自己初始化祖先就是自己 长度为格子总数
int res = 0 ;
public int numIslands(char[][] grid) {
int m = grid.length;
int n = grid[0].length;
p = new int[m*n];
//初始化 parent 数组,记录初始岛屿数(也就是 1 的数目)
for (int i = 0; i < m; i++)
for(int j = 0; j < n; j++){
if(grid[i][j]=='1') res++;
int idx = i*n + j;
p[idx] = idx;
}
for (int i = 0; i < m; i++)
for(int j = 0; j < n; j++){
int idx = i * n + j;
if(grid[i][j] == '1'){
//向下合并
if (i+1 < m && grid[i+1][j] == '1') { //合并岛屿
union(idx, (i + 1) * n + j);
}
//向右合并
if (j+1 <n && grid[i][j+1] == '1') {
union(idx, i * n + j + 1);
}
}
}
return res;
}
// 递归找祖先
int find(int i){
if (p[i] == i) return p[i];
return p[i] = find(p[i]);
}
void union(int i, int j){
if (find(i) == find(j)) return; //若祖先相同 则不做union操作
p[find(j)] = p[find(i)];//若祖先不同 ,说明之前没有同化过,则进行同化(修改被比较位置的祖先为当前待比较位置的祖先)
res--;//同化一次,res(1的总数) -1
}
以上三种方法这个B站的小姐姐讲的非常透彻
岛屿数量 Number of Islands—作者: 爱学习的饲养员