一文讲清楚字符串搜索问题【朴素法】和【KMP算法】

一、引入

字符串搜索问题是字符串中重要的一类问题，该问题可以描述为：给定字符串 str1 和 str2 ，找出字符串 str2 在 str1 中的出现位置（返回起始位置索引），如果 str2 不是 str1 中的连续子字符串则返回 -1。

我们今天主角—— KMP 算法可以在线性时间复杂内解决字符串搜索问题。在开始讲 KMP 算法之前，我们先来看一下朴素的字符串搜索方法是如何完成搜索任务的。

二、朴素解法

2.1 朴素法介绍

朴素的字符搜索算法从字符 str1[0] 开始与字符串 str2 进行匹配（匹配指的是判断对应字符是否相等），如果遇到无法匹配的字符，则需要从字符 str1[1] 开始与字符串 str2 进行匹配。如此匹配下去，直至找到 str2 在 str1 中出现的位置，如果没有则返回 -1。

2.2 图解朴素法

接下来以 str1 = "abbabc"，str2 = "abc" 为例，图文并茂进行解释。

①首先从 str1 中的首字符 'a' 开始与 str2 进行匹配，a=a、b=b、b!=c ，出现了字符不匹配的现象；

②从字符串 str1 的第二个字符开始进行匹配，b!=a；

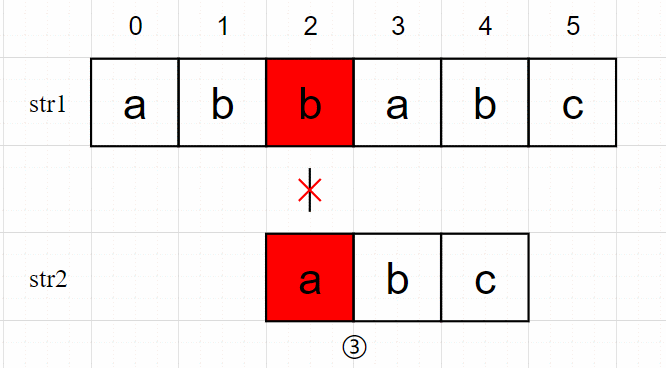
③从 str1[2] 字符开始进行匹配，b!=a；

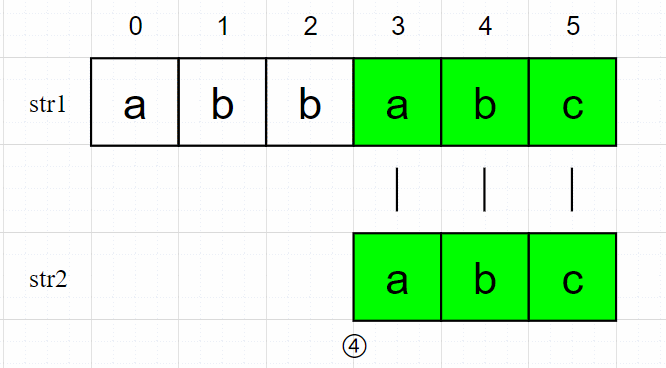
④从 str1[3] 开始匹配，a = a、b = b、c = c，于是找到了字符串 str2 在 str1 中的位置 3。

2.3 复杂度分析

时间复杂度：$O(n\times m)$，其中 $n$ 和 $m$ 分别为字符串 str1 和 str2 的长度。

空间复杂度：$O(1)$。

三、KMP算法

Knuth-Morris-Pratt字符串查找算法（简称为KMP算法）可在一个字符串S内查找一个词W的出现位置。一个词在不匹配时本身就包含足够的信息来确定下一个匹配可能的开始位置，此算法利用这一特性以避免重新检查先前配对的字符。

为了记录字符不匹配时的一些信息，首先需要了解真前缀、真后缀的定义。

前缀 指的是从字符串首位置开始到某个位置结束的连续子串，字符串 S 以 i 位置处字符结尾的前缀可以表示为 $Prefix(S,i)$，$Prefix(S,i)=S[\mathrm{0...}i]$。

真前缀 指的是除了 S 本身的 S 的前缀。

举例来说，字符串 abbad 的所有前缀为 {a, ab, abb, abba, abbad}，它的真前缀为 {a, ab, abb, abba}。

后缀 指的是从字符串某个位置 i 开始到整个字符串结束位置的连续子串， 字符串 S 以 i 位置开始的前缀可以表示为 $Suffix(S,i)$，$Suffix(S,i)=S[i...n-1]$，其中 $n$ 为字符串 S 的长度。

真后缀 指的是除了 S 本身的 S 的后缀。

举例来说，字符串 abbad 的所有后缀为 {d, ad, bad, bbad, abbad}，它的真后缀为 {d, ad, bad, bbad}。

3.1 nextArr 数组介绍

首先介绍 nextArr 数组，至于这个数组的用处，我们稍后再来说明。

字符串 str 的 nextArr 数组这样表示：长度与字符串 str 长度一样，nextArr[i] 表示在 str[i] 字符之前的字符串 str[0...i-1] 中，真后缀与真前缀的最大匹配（相等）长度是多少。

举例来说，str= "aaaab"，则nextArr[4]=3。str2[4]='b'，所以它之前的字符串为 "aaaa"，该字符串的真前缀和真后缀的最大匹配字符串为 "aaa"，长度为 3，所以 nextArr[4]=3。

我们先明白 nextArr 数组的概念即可，至于求解方法我们将在 3.3 节进行介绍。

3.2 图解 KMP 算法

3.2.1 原理

在理解了 nextArr 数组的含义之后，KMP 算法就很好理解了，为了方便表示，我们用图示的方式对字符搜索匹配进行解释。

①假设我们从 str1[i] 字符出发，匹配到 j 位置时发现字符不一致，如下图所示，str1[j] != str2[j-i]。

②我们计算字符串 str2 的 nextArr 数组，nextArr[j-i] 表示str2[0...j-i-1] 字符串真前缀和真后缀的最大匹配长度。假设真前缀为下图中 a 区域所示，真后缀为下图中 b 区域区域所示，a 区域后的第一个字符记为 str2[k]。

③在下一次检查中，可以直接从 str1[j] 与 str2[k] 处开始，不需要向朴素解法那样从 str1[i+1] 与 str2[0] 处开始。 因为直到 j 和 j-i 位置才有 str1[j] != str2[j-i]，所以 c 区域等于 b 区域，而 b 区域又和 a 区域是一样的，所以下一次匹配可以直接从 str1[j] 与 str2[k] 处开始（其实是从 c 区域开始位置与 str2 进行匹配，而 b 区域又和 a 区域是一样的，所以下一次匹配可以直接从 str1[j] 与 str2[k] 处开始）。

④现在有一个疑问，str1[i] 与 c 之间的区域为什么不用与字符串 str2 进行匹配，因为在这个区域中，从任何一个字符出发都匹配不出 str2。现在用反证法简单证明一下。

假设 str1[i] 与 c 之间的区域能与字符串 str2 匹配，那么 str1 中的 d 区域应该和以字符 str2[0] 开始的区域 e 匹配。现在假设 d 区域对应到 str2 中的区域为 d’，那么有 d = e = d'，因为 d' > b、e > a，所以我们现在找到了字符 str2[j-i] 之前字符串的更大的真前缀与真后缀匹配长度，这与 a、b 区域是最大的真前缀、真后缀匹配长度矛盾，所以原始的假设不成立，即str1[i] 与 c 之间的区域为什么不用与字符串 str2 进行匹配。

3.2.2 实现

经过以上的分析，我们知道了在进行字符搜索匹配的时候，遇到了 str2[j-i] 字符无法与 str1[j] 匹配时是利用 nextArr[j] 来加速匹配的。现在假设我们已经实现了求 nextArr 数组的函数 getNextArray()，利用该函数求字符串 str2 的 nextArr 数组并实现 KMP 算法。

先贴出代码，再进行分析：

// 判断字符串s2是否是字符串s1的子串，若是返回起始位置索引，否则返回 -1 
int kmp(string s1, string s2) {
  if(s1.size() == 0 || s2.size() == 0 || s1.size() < s2.size()) { // (0)
      return -1;
  }
  
  int i1 = 0, i2 = 0;
  vector<int> next = getNextArray(s2);	// (1)
  
  while (i1 < s1.size() && i2 < s2.size()) {
      if (s1[i1] == s2[i2]) {			    // (2)
          ++i1;
          ++i2;
      }
      else if (next[i2] == -1) {		    // (3) 字符串s2中的位置已经无法再往前跳了
          ++i1;
      }
      else {
          i2 = next[i2];                  // (4)
      }
  }
  return i2 == s2.size() ? i1 - i2 : -1;  // (5)
}

（0）一些特判的情况；

（1）通过 getNextArray(s2) 得到字符串 s2 的 nextArr 数组；

（2）利用双指针进行字符匹配，i1 指向字符 s1，i2 指向字符 s2，匹配上了就同时向右移动指针；

（3）next[i2] == -1 可以使用 i2 == 0 代替表示的含义都一样。此时指针 i2 指向了字符 s[0]，并且 s1[i1] != s2[0]，所以向 右移动 i1 指针，开始新的一轮匹配；

（4）指针 i2 跳到 s2[0...i2-1] 的真前缀的下一个字符开始匹配。

（5）最后，如果 i2 指针走完了字符串 s2，则返回 s2 在 s1 中首先出现的位置，否则表示 s2 是 s1 的连续子串。

3.3 nextArr 数组求解

我们已经明白了 nextArr 数组的概念及其存在的重要意义，接下来就来看看该数组到底应该怎么求。

字符串 s 的 nextArr 数组：表示的当前字符前面字符串的真前缀和真后缀的最大匹配长度。字符串 s 的 nextArr[0] = -1，因为字符 s[0] 之前没有任何字符，我们初始为 -1；nextArr[1] = 0，因为 s[1] 前面只有一个字符，一个字符没有真前缀和真后缀，所以为 0。

先贴出代码，再进行分析：

// nextArr数组计算
vector<int> getNextArray(string s) {
    if (s.size() == 1) {			// (0)
        return {-1};
    }
    
    int n = s.size();
    vector<int> next(n);
    next[0] = -1;
    next[1] = 0;
    int i = 2; 	// next数组的位置
    int cn = 0;	// 两层含义：1.最大匹配长度 2.真前缀后面第一个字符的位置（即将与s[i-1]字符比较的字符）
    
    while (i < n) {
        if (s[i-1] == s[cn]) {		// (1)
            // next[i++] = ++cn;
            next[i] = cnt + 1;
            ++i;
            ++cnt;
        }
        else if (cn > 0) {			// (2)
            cn = next[cn];
        }
        else {
            next[i++] = 0;			// (3)
        }
    }
    
    return next;
}

（0）字符串 s 长度为 1 时，nextArr = {-1}；否则长度 >= 2，next[1] = 0，接下来分析 n >= 3 时，nextArr 数组是如何更新的；

（1）i 表示当前要求 nextArr[i] 的位置，cn 有两层含义：一是指字符串真前缀与真后缀的最大匹配长度，二是指真前缀后面第一个字符位置。当在计算 nextArr[i] 时表明 nextArr[i-1] 已经计算得到，可以直接使用。

当 nextArr[i-1] = nextArr[cn] 时，表示此时 s[0...i-1] 中真前缀与真后缀的最大匹配字符串为 a 区域字符串加上 s[cn] 字符（b 区域字符串加上 s[i-1] 字符），最大匹配长度为 cn + 1，接下里需要将 i++、cn++ 为下一个位置的 nextArr 数组计算做准备。该情况下的执行代码可以等价替换为 nextArr[i++] = ++cnt;。

为什么要对 cn ++ 呢？因为 cn 始终表示的是真前缀后面第一个字符的位置。在计算下一个位置 nextArr[i+1] 时需要使用 nextArr[i]，nextArr[i] 的真前缀这时更新为 a 区域加上 s[cn] 字符了，所以即将与 s[i] 字符比较的字符就是 cn+1 位置的字符。

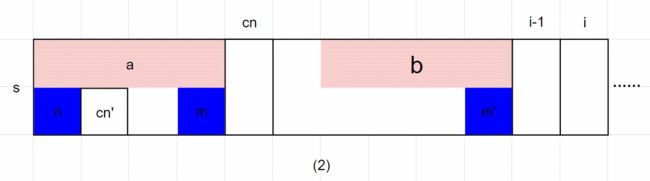
（2）当 nextArr[i-1] != nextArr[cn] 时，s[i-1] 将与新的 cn（图中的 cn'）进行比较。

下图中的 n、m 区域分别为 a 区域字符的真前缀和真后缀，于是有 m = n；图中 a 区域和 b 区域分别为字符串 s[0...i-1] 的真前缀和真后缀，于是有 m = m'，因此 n = m'；此时如果 s[i-1] = s[cn']，就有 nextArr[i] = cn' + 1，似乎与 (1) 中的判断类似，只是 cn 变成了 cn'，而恰好 cn' = nextArr[cn]（cn 的定义使然）。于是情况 (2) 只需要更新 cn 即可，判断让 (1) 处来做。

（3）此时若是 cn = 0 了，表示 s[0...i-1] 没有匹配的真前缀和真后缀，于是 nextArr[i] == 0，更新 i ++ 为计算下一个位置的 nextArr 数组做准备。

3.4 复杂度分析

求解字符串 s 的 nextArr 数组的时间复杂度为 $O(m)$，$m$ 是字符串的长度，空间复杂度为 $O(n)$。

KMP 算法的时间复杂度为 $O(n)$ ，$n$ 是搜索的原字符串的长度，空间复杂度为 $O(1)$。

四、总结

本篇博文主要讲述了字符串搜索算法中的朴素法和具有线性时间复杂度的 KMP 法。

KMP 算法的核心之处在于借助 nextArr 数组进行加速。

以上求解 nextArr 数组以及 KMP 算法的代码，可以作为模板进行记忆。对于此类经典的算法，一次看不懂不怕，就怕不坚持。

写在最后

以上就是本篇文章的内容了，感谢您的阅读。

如果感到有所收获的话可以给博主点一个 哦。

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出。