数据结构复习题(包含答案)
第一章 概论
一、选择题
1、研究数据结构就是研究( D )。
A. 数据的逻辑结构 B. 数据的存储结构
C. 数据的逻辑结构和存储结构 D. 数据的逻辑结构、存储结构及其基本操作
2、算法分析的两个主要方面是( A )。
A. 空间复杂度和时间复杂度 B. 正确性和简单性
C. 可读性和文档性 D. 数据复杂性和程序复杂性
3、具有线性结构的数据结构是( D )。
A. 图 B. 树 C. 广义表 D. 栈
4、计算机中的算法指的是解决某一个问题的有限运算序列,它必须具备输入、输出、( B )等5个特性。
A. 可执行性、可移植性和可扩充性 B. 可执行性、有穷性和确定性
C. 确定性、有穷性和稳定性 D. 易读性、稳定性和确定性
5、下面程序段的时间复杂度是( C )。
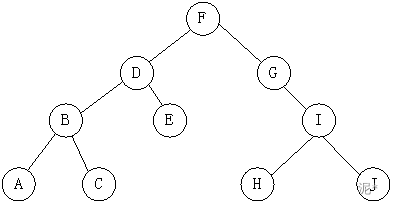
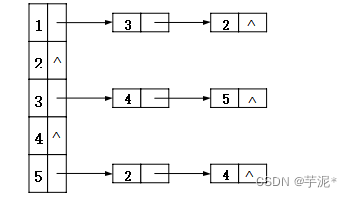
for(i=0;i for(j=0;j a[i][j]=i*j; A. O(m2) B. O(n2) C. O(m*n) D. O(m+n) 6、算法是( D )。 A. 计算机程序 B. 解决问题的计算方法 C. 排序算法 D. 解决问题的有限运算序列 7、某算法的语句执行频度为(3n+nlog2n+n2+8),其时间复杂度表示( C )。 A. O(n) B. O(nlog2n) C. O(n2) D. O(log2n) 8、下面程序段的时间复杂度为( C )。 i=1; while(i<=n) i=i*3; A. O(n) B. O(3n) C. O(log3n) D. O(n3) 9、数据结构是一门研究非数值计算的程序设计问题中计算机的数据元素以及它们之间的( B )和运算等的学科。 A. 结构 B. 关系 C. 运算 D. 算法 10、抽象数据类型的三个组成部分分别为( A)。 A. 数据对象、数据关系和基本操作 B. 数据元素、逻辑结构和存储结构 C. 数据项、数据元素和数据类型 D. 数据元素、数据结构和数据类型 11、通常从正确性、易读性、健壮性、高效性等4个方面评价算法的质量,以下解释错误的是( D )。 A. 正确性算法应能正确地实现预定的功能 B. 易读性算法应易于阅读和理解,以便调试、修改和扩充 C. 健壮性当环境发生变化时,算法能适当地做出反应或进行处理,不会产生不需要的运行结果 D. 高效性即达到所需要的时间性能 1、程序段“i=1;while(i<=n) i=i*2;”的时间复杂度为 O(n) 。 2、数据结构的四种基本类型中, 树形结构 的元素是一对多关系。 1、将数量级O(1),O(N),O(N2),O(N3),O(NLOG2N),O(LOG2N),O(2N)按增长率由小到大排序。 答案: O(1) O(log2N) O(N) O(Nlog2N) O(N2) O(N3) O(2N) 1、若长度为n的线性表采用顺序存储结构,在其第i个位置插入一个新元素算法的时间复杂度( )。 A. O(log2n) B.O(1) C. O(n) D.O(n2) 2、若一个线性表中最常用的操作是取第i个元素和找第i个元素的前趋元素,则采用( )存储方式最节省时间。 A. 顺序表 B. 单链表 C. 双链表 D. 单循环链表 3、具有线性结构的数据结构是( )。 A. 图 B. 树 C. 广义表 D. 栈 4、在一个长度为n的顺序表中,在第i个元素之前插入一个新元素时,需向后移动( )个元素。 A. n-i B. n-i+1 C. n-i-1 D. i 5、非空的循环单链表head的尾结点p满足( )。 A. p->next==head B. p->next==NULL C. p==NULL D. p==head 6、链表不具有的特点是( )。 A. 可随机访问任一元素 B. 插入删除不需要移动元素 C. 不必事先估计存储空间 D. 所需空间与线性表长度成正比 7、在双向循环链表中,在p指针所指的结点后插入一个指针q所指向的新结点,修改指针的操作是( )。 A. p->next=q;q->prior=p;p->next->prior=q;q->next=q; B. p->next=q;p->next->prior=q;q->prior=p;q->next=p->next; C. q->prior=p;q->next=p->next;p->next->prior=q;p->next=q; D. q->next=p->next;q->prior=p;p->next=q;p->next=q; 8、线性表采用链式存储时,结点的存储地址( )。 A. 必须是连续的 B. 必须是不连续的 C. 连续与否均可 D. 和头结点的存储地址相连续 9、在一个长度为n的顺序表中删除第i个元素,需要向前移动( )个元素。 A. n-i B. n-i+1 C. n-i-1 D. i+1 10、线性表是n个( )的有限序列。 A. 表元素 B. 字符 C. 数据元素 D. 数据项 11、从表中任一结点出发,都能扫描整个表的是( )。 A. 单链表 B. 顺序表 C. 循环链表 D. 静态链表 12、在具有n个结点的单链表上查找值为x的元素时,其时间复杂度为( )。 A. O(n) B. O(1) C. O(n2) D. O(n-1) 13、线性表L=(a1,a2,……,an),下列说法正确的是( )。 A. 每个元素都有一个直接前驱和一个直接后继 B. 线性表中至少要有一个元素 C. 表中诸元素的排列顺序必须是由小到大或由大到小 D. 除第一个和最后一个元素外,其余每个元素都由一个且仅有一个直接前驱和直接后继 14、一个顺序表的第一个元素的存储地址是90,每个元素的长度为2,则第6个元素的存储地址是( )。 A. 98 B. 100 C. 102 D. 106 15、在线性表的下列存储结构中,读取元素花费的时间最少的是( )。 A. 单链表 B. 双链表 C. 循环链表 D. 顺序表 16、在一个单链表中,若删除p所指向结点的后续结点,则执行( )。 A. p->next=p->next->next; B. p=p->next;p->next=p->next->next; C. p =p->next; D. p=p->next->next; 17、将长度为n的单链表连接在长度为m的单链表之后的算法的时间复杂度为( )。 A. O(1) B. O(n) C. O(m) D. O(m+n) 18、线性表的顺序存储结构是一种( )存储结构。 A. 随机存取 B. 顺序存取 C. 索引存取 D. 散列存取 19、顺序表中,插入一个元素所需移动的元素平均数是( )。 A. (n-1)/2 B. n C. n+1 D. (n+1)/2 10、循环链表的主要优点是( )。 A. 不再需要头指针 B. 已知某结点位置后能容易找到其直接前驱 C. 在进行插入、删除运算时能保证链表不断开 D. 在表中任一结点出发都能扫描整个链表 11、不带头结点的单链表head为空的判定条件是( A )。 A. head==NULL B. head->next==NULL C. head->next==head D. head!=NULL (B是带头结点的) 12、在下列对顺序表进行的操作中,算法时间复杂度为O(1)的是( )。 答案是A. 假设顺序表L,长度为n,求第i个节点L[i],直接前驱L[i-1],因此为O(1) 答案B需要移动n-i+1个节点,因此为O(n) 答案C也需要移动n-i个节点 答案D根据排序方法不同最慢O(n^2),最快O(nlogn) 13、已知指针p和q分别指向某单链表中第一个结点和最后一个结点。假设指针s指向另一个单链表中某个结点,则在s所指结点之后插入上述链表应执行的语句为( )。 A. q->next=s->next;s->next=p; B. s->next=p;q->next=s->next; C. p->next=s->next;s->next=q; D. s->next=q;p->next=s->next; 14、在以下的叙述中,正确的是( )。 A. 线性表的顺序存储结构优于链表存储结构 B. 线性表的顺序存储结构适用于频繁插入/删除数据元素的情况 C. 线性表的链表存储结构适用于频繁插入/删除数据元素的情况 D. 线性表的链表存储结构优于顺序存储结构 15、在表长为n的顺序表中,当在任何位置删除一个元素的概率相同时,删除一个元素所需移动的平均个数为( )。 A. (n-1)/2 B. n/2 C. (n+1)/2 D. n 16、在一个单链表中,已知q所指结点是p所指结点的前驱结点,若在q和p之间插入一个结点s,则执行( )。 A. s->next=p->next; p->next=s; B. p->next=s->next;s->next=p; C. q->next=s;s->next=p; D. p->next=s;s->next=q; 17、在单链表中,指针p指向元素为x的结点,实现删除x的后继的语句是( )。 A. p=p->next; B. p->next=p->next->next; C. p->next=p; D. p=p->next->next; 18、在头指针为head且表长大于1的单循环链表中,指针p指向表中某个结点,若p->next->next==head,则( )。 A. p指向头结点 B. p指向尾结点 C. p的直接后继是头结点 D. p的直接后继是尾结点 1、设单链表的结点结构为(data,next)。已知指针p指向单链表中的结点,q指向新结点,欲将q插入到p结点之后,则需要执行的语句: ; 。 答案:q->next=p->next p->next=q 2、线性表的逻辑结构是 ,其所含元素的个数称为线性表的 。 答案:线性结构 长度 3、写出带头结点的双向循环链表L为空表的条件 。 答案:L->prior==L->next==L 4、带头结点的单链表head为空的条件是 。 答案:head->next==NULL 5、在一个单链表中删除p所指结点的后继结点时,应执行以下操作: q = p->next; p->next= _ q->next ___; 1、单链表不是一种随机存储结构。 ✔️ 2、在具有头结点的单链表中,头指针指向链表的第一个数据结点。❌ 3、用循环单链表表示的链队列中,可以不设队头指针,仅在队尾设置队尾指针。✔️ 4、顺序存储方式只能用于存储线性结构。❌ 5、在线性表的顺序存储结构中,逻辑上相邻的两个元素但是在物理位置上不一定是相邻的。❌ 6、链式存储的线性表可以随机存取。❌ 四、程序分析填空题 1、函数GetElem实现返回单链表的第i个元素,请在空格处将算法补充完整。 int GetElem(LinkList L,int i,Elemtype *e){ LinkList p;int j; p=L->next;j=1; while(p&&j (1) ;++j; } if(!p||j>i) return ERROR; *e= (2) ; return OK; } 答案:(1)p=p->next (2)p->data 2、函数实现单链表的插入算法,请在空格处将算法补充完整。 int ListInsert(LinkList L,int i,ElemType e){ LNode *p,*s;int j; p=L;j=0; while((p!=NULL)&&(j if(p==NULL||j>i-1) return ERROR; s=(LNode *)malloc(sizeof(LNode)); s->data=e; (1) ; (2) ; return OK; }/*ListInsert*/ 答案:(1)s->next=p->next (2)p->next=s 3、函数ListDelete_sq实现顺序表删除算法,请在空格处将算法补充完整。 int ListDelete_sq(Sqlist *L,int i){ int k; if(i<1||i>L->length) return ERROR; for(k=i-1;k L->elem[k]= (1) ; (2) ; return OK; } 答案:(1)L->elem[k+1] (2) --L->Length 4、函数实现单链表的删除算法,请在空格处将算法补充完整。 int ListDelete(LinkList L,int i,ElemType *s){ LNode *p,*q; int j; p=L;j=0; while(( (1) )&&(j p=p->next;j++; } if(p->next==NULL||j>i-1) return ERROR; q=p->next; (2) ; *s=q->data; free(q); return OK; }/*listDelete*/ 答案:(1)p->next!=NULL (2)p->next=q->next 5、写出算法的功能。 int L(head){ node * head; int n=0; node *p; p=head; while(p!=NULL) { p=p->next; n++; } return(n); } 答案:求单链表head的长度 1、有两个循环链表,链头指针分别为L1和L2,要求写出算法将L2链表链到L1链表之后,且连接后仍保持循环链表形式。 答案:void merge(Lnode *L1, Lnode *L2) {Lnode *p,*q ; while(p->next!=L1) p=p->next; while(q->next!=L2) q=q->next; q->next=L1; p->next =L2; } 2、设一个带头结点的单向链表的头指针为head,设计算法,将链表的记录,按照data域的值递增排序。 答案:void assending(Lnode *head) {Lnode *p,*q , *r, *s; p=head->next; q=p->next; p->next=NULL; while(q) {r=q; q=q->next; if(r->data<=p->data) {r->next=p; head->next=r; p=r; } else {while(!p && r->data>p->data) {s=p; p=p->next; } r->next=p; s->next=r;} p=head->next; } } 3、编写算法,将一个头指针为head不带头结点的单链表改造为一个单向循环链表,并分析算法的时间复杂度。 答案: void linklist_c(Lnode *head) {Lnode *p; p=head; if(!p) return ERROR; while(p->next!=NULL) p=p->next; p->next=head; } 设单链表的长度(数据结点数)为N,则该算法的时间主要花费在查找链表最后一个结点上(算法中的while循环),所以该算法的时间复杂度为O(N)。 4、假设线性表采用顺序存储结构,表中元素值为整型。阅读算法f2,设顺序表L=(3,7,3,2,1,1,8,7,3),写出执行算法f2后的线性表L的数据元素,并描述该算法的功能。 void f2(SeqList *L){ int i,j,k; k=0; for(i=0;i for(j=0;j if(j==k){ if(k!=i)L->data[k]=L->data[i]; k++; } } L->length=k; } 答案: (3,7,2,1,8) 删除顺序表中重复的元素 1、一个栈的输入序列为:a,b,c,d,e,则栈的不可能输出的序列是( )。 A. a,b,c,d,e B. d,e,c,b,a C. d,c,e,a,b D. e,d,c,b,a 2、判断一个循环队列Q(最多n个元素)为满的条件是( )。 A. Q->rear==Q->front B. Q->rear==Q->front+1 C. Q->front==(Q->rear+1)%n D. Q->front==(Q->rear-1)%n 3、设计一个判别表达式中括号是否配对的算法,采用( )数据结构最佳。 A. 顺序表 B. 链表 C. 队列 D. 栈 4、带头结点的单链表head为空的判定条件是( )。 A. head==NULL B. head->next==NULL C. head->next!=NULL D. head!=NULL 5、一个栈的输入序列为:1,2,3,4,则栈的不可能输出的序列是( )。 A. 1243 B. 2134 C. 1432 D. 4312 E. 3214 6、若用一个大小为6的数组来实现循环队列,且当rear和front的值分别为0,3。当从队列中删除一个元素,再加入两个元素后,rear和front的值分别为( )。 A. 1和5 B. 2和4 C. 4和2 D. 5和1 7、队列的插入操作是在( )。 A. 队尾 B. 队头 C. 队列任意位置 D. 队头元素后 8、循环队列的队头和队尾指针分别为front和rear,则判断循环队列为空的条件是( )。 A. front==rear B. front==0 C. rear==0 D. front=rear+1 9、一个顺序栈S,其栈顶指针为top,则将元素e入栈的操作是( )。 A. *S->top=e;S->top++; B. S->top++;*S->top=e; C. *S->top=e D. S->top=e; 10、将递归算法转换成对应的非递归算法时,通常需要使用( )来保存中间结果。 A. 队列 B. 栈 C. 链表 D. 树 11、栈的插入和删除操作在( )。 A. 栈底 B. 栈顶 C. 任意位置 D. 指定位置 12、五节车厢以编号1,2,3,4,5顺序进入铁路调度站(栈),可以得到( )的编组。 A. 3,4,5,1,2 B. 2,4,1,3,5 C. 3,5,4,2,1 D. 1,3,5,2,4 13、判定一个顺序栈S(栈空间大小为n)为空的条件是( )。 A. S->top==0 B. S->top!=0 C. S->top==n D. S->top!=n 14、在一个链队列中,front和rear分别为头指针和尾指针,则插入一个结点s的操作为( )。 A. front=front->next B. s->next=rear;rear=s C. rear->next=s;rear=s; D. s->next=front;front=s; 15、一个队列的入队序列是1,2,3,4,则队列的出队序列是( )。 A. 1,2,3,4 B. 4,3,2,1 C. 1,4,3,2 D. 3,4,1,2 16、依次在初始为空的队列中插入元素a,b,c,d以后,紧接着做了两次删除操作,此时的队头元素是( )。 A. a B. b C. c D. d 17、正常情况下,删除非空的顺序存储结构的堆栈的栈顶元素,栈顶指针top的变化是( )。 A. top不变 B. top=0 C. top=top+1 D. top=top-1 18、判断一个循环队列Q(空间大小为M)为空的条件是( A )。 A. Q->front==Q->rear B. Q->rear-Q->front-1==M C. Q->front+1=Q->rear D. Q->rear+1=Q->front 19、设计一个判别表达式中左右括号是否配对出现的算法,采用( C )数据结构最佳。 A. 线性表的顺序存储结构 B. 队列 C. 栈 D. 线性表的链式存储结构 20、当用大小为N的数组存储顺序循环队列时,该队列的最大长度为(C )。 A. N B. N+1 C. N-1 D. N-2 21、队列的删除操作是在( A )。 A. 队首 B. 队尾 C. 队前 D. 队后 22、若让元素1,2,3依次进栈,则出栈次序不可能是( C )。 A. 3,2,1 B. 2,1,3 C. 3,1,2 D. 1,3,2 23、循环队列用数组A[0,m-1]存放其元素值,已知其头尾指针分别是front和rear,则当前队列中的元素个数是( A )。 A. (rear-front+m)%m B. rear-front+1 C. rear-front-1 D. rear-front 24、栈和队列都是(C )。 A. 链式存储的线性结构 B. 链式存储的非线性结构 C. 限制存取点的线性结构 D. 限制存取点的非线性结构 25、在一个链队列中,假定front和rear分别为队头指针和队尾指针,删除一个结点的操作是( A )。 A. front=front->next B. rear= rear->next C. rear->next=front D. front->next=rear 26、队和栈的主要区别是( D )。 A. 逻辑结构不同 B. 存储结构不同 C. 所包含的运算个数不同 D. 限定插入和删除的位置不同 1、设栈S和队列Q的初始状态为空,元素e1,e2,e3,e4,e5,e6依次通过栈S,一个元素出栈后即进入队列Q,若6个元素出队的序列是e2,e4,e3,e6,e5,e1,则栈的容量至少应该是 。 答案:3 2、一个循环队列Q的存储空间大小为M,其队头和队尾指针分别为front和rear,则循环队列中元素的个数为: 。 答案:(rear-front+M)%M 3、在具有n个元素的循环队列中,队满时具有 个元素。 答案:n-1 4、设循环队列的容量为70,现经过一系列的入队和出队操作后,front为20,rear为11,则队列中元素的个数为 。 答案:61 5、已知循环队列的存储空间大小为20,且当前队列的头指针和尾指针的值分别为8和3,且该队列的当前的长度为____15___。 1、栈和队列都是受限的线性结构。✔️ 2、在单链表中,要访问某个结点,只要知道该结点的地址即可;因此,单链表是一种随机存取结构。❌ 3、以链表作为栈的存储结构,出栈操作必须判别栈空的情况。✔️ 1、已知栈的基本操作函数: int InitStack(SqStack *S); //构造空栈 int StackEmpty(SqStack *S);//判断栈空 int Push(SqStack *S,ElemType e);//入栈 int Pop(SqStack *S,ElemType *e);//出栈 函数conversion实现十进制数转换为八进制数,请将函数补充完整。 void conversion(){ InitStack(S); scanf(“%d”,&N); while(N){ (1) ; N=N/8; } while( (2) ){ Pop(S,&e); printf(“%d”,e); } }//conversion 答案:(1)Push(S,N%8) (2)!StackEmpty(S) 2、写出算法的功能。 int function(SqQueue *Q,ElemType *e){ if(Q->front==Q->rear) return ERROR; *e=Q->base[Q->front]; Q->front=(Q->front+1)%MAXSIZE; return OK; } 若循环队列非空,队头元素出队列且返回其值,否则返回空元素。 3、阅读算法f2,并回答下列问题: (1)设队列Q=(1,3,5,2,4,6)。写出执行算法f2后的队列Q; (2)简述算法f2的功能。 void f2(Queue *Q){ DataType e; if (!QueueEmpty(Q)){ e=DeQueue(Q); f2(Q); EnQueue(Q,e); } } 答案:(1)6,4,2,5,3,1 (2)将队列倒置 1、假设以带头结点的循环链表表示队列,并且只设一个指针指向队尾结点,但不设头指针,请写出相应的入队列算法(用函数实现)。 答案:void EnQueue(Lnode *rear, ElemType e) { Lnode *new; New=(Lnode *)malloc(sizeof(Lnode)); If(!new) return ERROR; new->data=e; new->next=rear->next; rear->next=new; rear =new; } 2、对于一个栈,给出输入项A,B,C,D,如果输入项序列为A,B,C,D,试给出全部可能的输出序列。 4,1,4,1,2,1,1 答案:出栈的可能序列: ABCD ABDC ACDB ACBD ADCB BACD BADC BCAD BCDA BDCA CBDA CBAD CDBA DCBA 1、设有两个串S1和S2,求串S2在S1中首次出现位置的运算称作( C )。 A. 连接 B. 求子串 C. 模式匹配 D. 判断子串 2、串与普通的线性表相比较,它的特殊性体现在( C )。 A. 顺序的存储结构 B. 链式存储结构 C. 数据元素是一个字符 D. 数据元素任意 3、空串和空格串( B )。 A. 相同 B. 不相同 C. 可能相同 D. 无法确定 4、与线性表相比,串的插入和删除操作的特点是( B )。 A. 通常以串整体作为操作对象 B. 需要更多的辅助空间 C. 算法的时间复杂度较高 D. 涉及移动的元素更多 5、设SUBSTR(S,i,k)是求S中从第i个字符开始的连续k个字符组成的子串的操作,则对于S=‘Beijing&Nanjing’,SUBSTR(S,4,5)=( B )。 A. ‘ijing’ B. ‘jing&’ C. ‘ingNa’ D. ‘ing&N’ 二、填空题 1、求子串在主串中首次出现的位置的运算称为 模式匹配 。 2、设s=‘I︺AM︺A︺TEACHER’,其长度是__14__。 3、两个串相等的充分必要条件是两个串的长度相等且 对应位置字符相同 。 四、程序填空题 1、函数实现串的模式匹配算法,请在空格处将算法补充完整。 int index_bf(sstring *s,sstring *t,int start){ int i=start-1,j=0; while(i if(s->data[i]==t->data[j]){ i++;j++; }else{ i= i-j+1 ;j=0; } if(j>=t->len) return i-t->len+1 ; else return -1; }} 2、写出下面算法的功能。 int function(SqString *s1,SqString *s2){ int i; for(i=0;i if(s->data[i]!=s2->data[i]) return s1->data[i]-s2->data[i]; return s1->length-s2->length; } 答案:.串比较算法 3、写出算法的功能。 int fun(sqstring *s,sqstring *t,int start){ int i=start-1,j=0; while(i if(s->data[i]==t->data[j]){ i++;j++; }else{ i=i-j+1;j=0; } if(j>=t->len) return i-t->len+1; else return -1; } 答案:串的模式匹配算法 1、数组A[0..5,0..6]的每个元素占5个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5][5]的地址是(A )。 A. 1175 B. 1180 C. 1205 D. 1210 2、常对数组进行两种基本操作是( C )。 A. 建立和删除 B. 索引和修改 C. 查找和修改 D. 查找与索引 3、对一些特殊矩阵采用压缩存储的目的主要是为了( D )。 A. 表达变得简单 B. 对矩阵元素的存取变得简单 C. 去掉矩阵中的多余元素 D. 减少不必要的存储空间的开销 (√ )1、稀疏矩阵压缩存储后,必会失去随机存取功能。 1、已知二维数组A[m][n]采用行序为主方式存储,每个元素占k个存储单元,并且第一个元素的存储地址是LOC(A[0][0]),则A[i][j]的地址是___ Loc(A[0][0])+(i*N+j)*k ____。 2、二维数组,可以按照 列序为主和行序为主 两种不同的存储方式。 3、稀疏矩阵的压缩存储方式有: 三元组 和 十字链表 。 1、二叉树的深度为k,则二叉树最多有( C )个结点。 A. 2k B. 2k-1 C. 2k-1 D. 2k-1 2、用顺序存储的方法,将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..N]中,若结点R[i]有右孩子,则其右孩子是( B )。 A. R[2i-1] B. R[2i+1] C. R[2i] D. R[2/i] 3、设a,b为一棵二叉树上的两个结点,在中序遍历时,a在b前面的条件是( B )。 A. a在b的右方 B. a在b的左方 C. a是b的祖先 D. a是b的子孙 4、设一棵二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树先序遍历序列为( D )。 A. adbce B. decab C. debac D. abcde 5、在一棵具有5层的满二叉树中结点总数为( A )。 A. 31 B. 32 C. 33 D. 16 6、由二叉树的前序和后序遍历序列( B )惟一确定这棵二叉树。 A. 能 B. 不能 7、某二叉树的中序序列为ABCDEFG,后序序列为BDCAFGE,则其左子树中结点数目为( C )。 A. 3 B. 2 C. 4 D. 5 8、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为( C )。 A. 67 B. 68 C. 69 D. 70 9、将一棵有100个结点的完全二叉树从根这一层开始,每一层上从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为( A )。 A. 98 B. 99 C. 50 D. 48 10、对某二叉树进行先序遍历的结果为ABDEFC,中序遍历的结果为DBFEAC,则后序遍历的结果是( B )。 A. DBFEAC B. DFEBCA C. BDFECA D. BDEFAC 11、树最适合用来表示( C )。 A. 有序数据元素 B. 无序数据元素 C. 元素之间具有分支层次关系的数据 D. 元素之间无联系的数据 12、在线索二叉树中,t所指结点没有左子树的充要条件是(B )。 A. t->left==NULL B. t->ltag==1 C. t->ltag==1&&t->left==NULL D. 以上都不对 13、假定在一棵二叉树中,度为2的结点数为15,度为1的结点数为30,则叶子结点数为( B )个。 A. 15 B. 16 C. 17 D. 47 14、在下列情况中,可称为二叉树的是( B )。 A. 每个结点至多有两棵子树的树 B. 哈夫曼树 C. 每个结点至多有两棵子树的有序树 D. 每个结点只有一棵子树 15、用顺序存储的方法,将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..n]中,若结点R[i]有左孩子,则其左孩子是(C )。 A. R[2i-1] B. R[2i+1] C. R[2i] D. R[2/i] 16、下面说法中正确的是( D )。 A. 度为2的树是二叉树 B. 度为2的有序树是二叉树 C. 子树有严格左右之分的树是二叉树 D. 子树有严格左右之分,且度不超过2的树是二叉树 17、按照二叉树的定义,具有3个结点的二叉树有( C )种。 A. 3 B. 4 C. 5 D. 6 18、由权值为3,6,7,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为( A )。 A. 51 B. 23 C. 53 D. 74 ( √)1、存在这样的二叉树,对它采用任何次序的遍历,结果相同。 (× )4、在哈夫曼编码中,当两个字符出现的频率相同时,其编码也相同,对于这种情况应做特殊处理。 (√ )5、一个含有n个结点的完全二叉树,它的高度是ëlog2nû+1。 (√ )6、完全二叉树的某结点若无左孩子,则它必是叶结点。 1、具有n个结点的完全二叉树的深度是 ëlog2nû+1 。 2、哈夫曼树是其树的带权路径长度 最小 的二叉树。 3、在一棵二叉树中,度为0的结点的个数是n0,度为2的结点的个数为n2,则有n0= N2+1 。 4、树内各结点度的 最大值 称为树的度。 1、函数InOrderTraverse(Bitree bt)实现二叉树的中序遍历,请在空格处将算法补充完整。 void InOrderTraverse(BiTree bt){ if( ){ InOrderTraverse(bt->lchild); printf(“%c”,bt->data); ; } } 2、函数depth实现返回二叉树的高度,请在空格处将算法补充完整。 int depth(Bitree *t){ if(t==NULL) return 0; else{ hl=depth(t->lchild); hr= depth(t->rchild) ; if( hl>hr ) return hl+1; else return hr+1; } } 3、写出下面算法的功能。 int LeafNodeCount(BiTree T) { if(T==NULL) return 0; //如果是空树,则叶子结点个数为0 else if(T->lchild==NULL&&T->rchild==NULL) return 1; else return LeafNodeCount(T->lchild)+LeafNodeCount(T->rchild); } 答案:统计二叉树的叶结点个数 1、假设一棵二叉树的先序序列为EBADCFHGIKJ,中序序列为ABCDEFGHIJK,请画出该二叉树。 2、假设用于通讯的电文仅由8个字母A、B、C、D、E、F、G、H组成,字母在电文中出现的频率分别为:0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.10。请为这8个字母设计哈夫曼编码。 3、已知二叉树的先序遍历序列为ABCDEFGH,中序遍历序列为CBEDFAGH,画出二叉树。 答案:二叉树形态 4、试用权集合{12,4,5,6,1,2}构造哈夫曼树,并计算哈夫曼树的带权路径长度。 WPL=12*1+(4+5+6)*3+(1+2)*4=12+45+12=69 5、已知权值集合为{5,7,2,3,6,9},要求给出哈夫曼树,并计算带权路径长度WPL。 (2)带权路径长度:WPL=(6+7+9)*2+5*3+(2+3)*4=44+15+20=79 6、已知一棵二叉树的先序序列:ABDGJEHCFIKL;中序序列:DJGBEHACKILF。画出二叉树的形态。 7、一份电文中有6种字符:A,B,C,D,E,F,它们的出现频率依次为16,5,9,3,30,1,完成问题: (1)设计一棵哈夫曼树;(画出其树结构) (2)计算其带权路径长度WPL; (2)带权路径长度:WPL=30*1+16*2+9*3+5*4+(1+3)*5=30+32+27+20+20=129 8、已知某森林的二叉树如下所示,试画出它所表示的森林。 答案: 9、如下所示的二叉树,请写出先序、中序、后序遍历的序列。 答案:先序:FDBACEGIHJ 中序:ABCDEFGHIJ 后序:ACBEDHJIGF 1、编写求一棵二叉树中结点总数的算法。 1、对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为( )。 A. n B. n2 C. n-1 D. (n-1)2 2、如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是( )。 A. 完全图 B. 连通图 C. 有回路 D. 一棵树 3、带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中( )。 A. 第i行非无穷的元素之和 B. 第i列非无穷的元素个数之和 C. 第i行非无穷且非0的元素个数 D. 第i行与第i列非无穷且非0的元素之和 4、采用邻接表存储的图,其深度优先遍历类似于二叉树的( )。 A. 中序遍历 B. 先序遍历 C. 后序遍历 D. 按层次遍历 5、无向图的邻接矩阵是一个( )。 A. 对称矩阵 B. 零矩阵 C. 上三角矩阵 D. 对角矩阵 6、邻接表是图的一种( )。 A. 顺序存储结构 B. 链式存储结构 C. 索引存储结构 D. 散列存储结构 7、在无向图中定义顶点vi与vj之间的路径为从vi到vj的一个( )。 A. 顶点序列 B. 边序列 C. 权值总和 D. 边的条数 8、在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有( )邻接点。 A. 入边 B. 出边 C. 入边和出边 D. 不是出边也不是入边 9、设G1=(V1,E1)和G2=(V2,E2)为两个图,如果V1ÍV2,E1ÍE2则称( )。 A. G1是G2的子图 B. G2是G1的子图 C. G1是G2的连通分量 D. G2是G1的连通分量 10、已知一个有向图的邻接矩阵表示,要删除所有从第i个结点发出的边,应( )。 A. 将邻接矩阵的第i行删除 B. 将邻接矩阵的第i行元素全部置为0 C. 将邻接矩阵的第i列删除 D. 将邻接矩阵的第i列元素全部置为0 11、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的( )倍。 A. 1/2 B. 1 C. 2 D. 4 12、下列关于图遍历的说法不正确的是( )。 A. 连通图的深度优先搜索是一个递归过程 B. 图的广度优先搜索中邻接点的寻找具有“先进先出”的特征 C. 非连通图不能用深度优先搜索法 D. 图的遍历要求每一顶点仅被访问一次 13、带权有向图G用邻接矩阵A存储,则顶点i的入度为A中:( )。 A. 第i行非¥的元素之和 B. 第i列非¥的元素之和 C. 第i行非¥且非0的元素个数 D. 第i列非¥且非0的元素个数 14、采用邻接表存储的图的广度优先遍历算法类似于二叉树的( )。 A. 先序遍历 B. 中序遍历 C. 后序遍历 D. 按层次遍历 15、一个具有n个顶点的有向图最多有( )条边。 A. n×(n-1)/2 B. n×(n-1) C. n×(n+1)/2 D. n2 16、已知一个有向图的邻接表存储结构如图所示,根据深度优先遍历算法,从顶点v1出发,所得到的顶点序列是( )。 A. v1,v2,v3,v5,v4 B. v1,v2,v3,v4,v5 C. v1,v3,v4,v5,v2 D. v1,v4,v3,v5,v2 17、以下说法正确的是( )。 A. 连通分量是无向图中的极小连通子图 B. 强连通分量是有向图中的极大强连通子图 C. 在一个有向图的拓扑序列中若顶点a在顶点b之前,则图中必有一条弧 D. 对有向图G,如果以任一顶点出发进行一次深度优先或广度优先搜索能访问到每个顶点,则该图一定是完全图 18、假设有向图含n个顶点及e条弧,则表示该图的邻接表中包含的弧结点个数为( )。 A. n B. e C. 2e D. n*e 19、设图的邻接矩阵为,则该图为( )。 A. 有向图 B. 无向图 C. 强连通图 D. 完全图 20、任何一个无向连通图的最小生成树( )种。 A. 只有一棵 B. 有一棵或多棵 C. 一定有多棵 D. 可能不存在 21、已知一有向图的邻接表存储结构如图所示,根据有向图的广度优先遍历算法,从顶点v1出发,所得到的顶点序列是( )。 A. v1,v2,v3,v4,v5 B. v1,v3,v2,v4,v5 C. v1,v2,v3,v5,v4 D. v1,v4,v3,v5,v2 22、对于一个有向图,若一个顶点的入度为k1,、出度为k2,则对应邻接表中该顶点单链表中的结点数为( )。 A. k1 B. k2 C. k1+k2 D. k1-k2 22、一个具有8个顶点的有向图中,所有顶点的入度之和与所有顶点的出度之和的差等于( )。 A. 16 B. 4 C. 0 D. 2 23、无向图中一个顶点的度是指图中( )。 A. 通过该顶点的简单路径数 B. 与该顶点相邻接的顶点数 C. 与该顶点连通的顶点数 D. 通过该顶点的回路数 1、n个顶点的连通图至少有 边。 答案:n-1条 2、一个连通图的生成树是一个 ,它包含图中所有顶点,但只有足以构成一棵树的n-1条边。 答案:极小连通子图 3、一个图的 表示法是惟一的。 答案:邻接矩阵 4、遍历图的基本方法有深度优先搜索和广度优先搜索,其中 是一个递归过程。 答案:深度优先搜索 5、在无向图G的邻接矩阵A中,若A[i][j]等于1,则A[j][i]等于 。 答案:1 6、已知一个图的邻接矩阵表示,计算第i个结点的入度的方法是 求第i列的和 。 7、n个顶点的无向图最多有 边。 8、已知一个图的邻接矩阵表示,删除所有从第i个结点出发的边的方法是 将第I行和第I列的值全部更新为零)。 。 9、若以邻接矩阵表示有向图,则邻接矩阵上第i行中非零元素的个数即为顶点vi的 。 1、图的连通分量是无向图的极小连通子图。 O 2、一个图的广度优先搜索树是惟一的。O 3、图的深度优先搜索序列和广度优先搜索序列不是惟一的。P 4、邻接表只能用于存储有向图,而邻接矩阵则可存储有向图和无向图。O 5、存储图的邻接矩阵中,邻接矩阵的大小不但与图的顶点个数有关,而且与图的边数也有关。O 6、邻接表只能用于存储有向图,而邻接矩阵则可存储有向图和无向图。O 7、图的生成树是惟一的。O 1、写出下面算法的功能。 typedef struct{ int vexnum,arcnum; char vexs[N]; int arcs[N][N]; }graph; void funtion(int i,graph *g){ int j; printf("node:%c\n",g->vexs[i]); visited[i]=TRUE; for(j=0;j function(j,g); } 答案:实现图的深度优先遍历算法 1、已知图G的邻接矩阵如下所示: 求从顶点1出发的广度优先搜索序列; 答案:(1)广度优先遍历序列:1; 2, 3, 4; 5; 6 2、设一个无向图的邻接矩阵如下图所示: (1)画出该图; (2)画出从顶点0出发的深度优先生成树; 答案: (1)图形态 (2)深度优先搜索树 二、填空题
三、综合题
第二章 线性表
一、选择题
二、填空题
三、判断题
五、综合题
第三章 栈和队列
一、选择题
二、填空题
三、判断题
四、程序分析填空题
五、综合题
第四章 串
一、选择题
数组
一、选择题
二、判断题
三、填空题
第六章 树
一、选择题
二、判断题
三、填空题
四、代码填空题
五、综合题
六、编程题
第七章 图
一、选择题
二、填空题
三、判断题
四、程序分析题
五、综合题