leetcode_刷题总结(c++)_回溯法
主要参考博客:
DFS–基本入门模板 和 例题 (绝对入门) (最全)
C++ 总结了回溯问题类型 带你搞懂回溯算法(大量例题)
排列用visited数组标记选用状态,组合(搜索)用index标记可选集的起始索引
文章目录
- 回溯法
- 模板
- leetcode部分题目
-
- (一)数组
-
- 46. 全排列
- 47. 全排列 II
- 剑指 Offer 38. 字符串的排列
- 39. 组合总和
- 40. 组合总和 II
- 78. 子集
- 90. 子集 II
- 473. 火柴拼正方形
- (二)二维数组/字符串
-
- 79. 单词搜索
- 62. 不同路径
- 51. N 皇后
- 37. 解数独
- (三)其他
-
- 22. 括号生成
回溯法
大部分回溯法的题目都能通过DFS的模板写出来。
从数据类型方面 可以将DFS题分为两大类:
1 . 地图型:这种题型将地图输入,要求完成一定的任务。因为地图的存在。使得题意清楚形象化,容易理清搜索思路。
2 . 数据型:这种题型没有给定地图,一般是一串数字或字母,要求按照一定的任务解题。相对于地图型,这种题型较为抽象,需要在数据中进行搜索。数据以数组的形式存储,那么只要将数组也当作一张图来进行搜索就可以了。
回溯问题的类型
子集、组合: 子集、子集 II、组合、组合总和、组合总和 II
全排列: 全排列、全排列 II、字符串的全排列、字母大小写全排列
搜索: 解数独、单词搜索、N皇后、分割回文串、二进制手表
注意:子集、组合与排列是不同性质的概念。子集、组合是无关顺序的,而排列是和元素顺序有关的,如 [1,2] 和 [2,1] 是同一个组合(子集),但 [1,2] 和 [2,1] 是两种不一样的排列!!!!因此被分为两类问题
需要注意的点:
1、是否需要按一定的顺序选择
如果需要的话可以代码中加入选择index
2、dfs处理void返回,也可以返回bool类型
模板
void dfs()//参数用来表示状态
{
if(到达终点状态)
{
...//根据题意添加
return;
}
if(越界或者是不合法状态)
return;
if(特殊状态)//剪枝
return ;
for(扩展方式)
{
if(扩展方式所达到状态合法)
{
修改操作;//根据题意来添加
标记;
dfs();
(还原标记);
//是否还原标记根据题意
//如果加上(还原标记)就是 回溯法
}
}
}
leetcode部分题目
(一)数组
一般要对数组进行排序,方便剪枝优化
排序:将相同的元素放在一起,这样在重复时就能和前一个元素进行比较(是否已经使用过,如果是完全相同的元素,且之间已经使用过,则可以直接跳过),从而可以达到剪枝的效果。
这里是伪代码
//需要排序
sort(nums.begin(),nums.end());
//1、元素可以重复使用!但是重复排列不行(这就需要给定搜索空间(index,n) )!
//注意 元素可以重复使用 下一次的搜索空间 相同
//但是这样可以确保它不会往回搜索 导致重复排列
//for循环从0开始
if(i>0 && nums[i-1]==nums[i]){
continue;
}
dfs(i,nums);
//2、元素不可以重复使用!重复排列不行
//方法一: for循环从[index,n)=>给定搜索空间(index,n)
if(i>index && nums[i-1]==nums[i]){
continue;
}
dfs(i+1,nums);
//3、元素不可以重复使用!
//方法二:for循环从[0,n) used数组标记
if(i>0 && nums[i-1]==nums[i] && used[i-1] == true){
continue;
}
dfs(nums);
如果题目给定不含重复数字的数组,则这一句可以不写
46. 全排列
class Solution {
public:
vector<int> cur;
vector<vector<int>> result;
void dfs(vector<int>& nums, vector<bool>& used) {
if (cur.size() == nums.size()){//到达终点状态
result.push_back(cur);
return;
}
for(int i = 0; i < nums.size(); i++){
if(used[i] == true) //已经访问过 跳过
continue;
used[i] = true;//标记
cur.push_back(nums[i]);
dfs(nums, used);
cur.pop_back();
used[i] = false;//还原标记
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
cur.clear();
vector<bool> used(nums.size(), false);
dfs(nums, used);
return result;
}
};
47. 全排列 II
元素不能重复使用,nums包含重复数字,
且不能出现重复排列
思路:
因为题目给出不能出现元素重复的排列,故需要进行去重操作。
class Solution {
public:
vector<int> cur;
vector<vector<int>> result;
void dfs(vector<int>& nums, vector<bool>& used){
// 此时说明找到了一组
if(cur.size() == nums.size()){
result.push_back(cur);
return;
}
for(int i = 0; i < nums.size(); i++){
//剪枝
if(used[i] == true)
continue;
//是否已经使用过,如果是完全相同的元素,且之间已经使用过,则可以直接跳过
if(i>0 && nums[i]==nums[i-1] && used[i-1] == true)
continue;
used[i] = true;//标记
cur.push_back(nums[i]);
dfs(nums, used);
cur.pop_back();
used[i] = false;//还原标记
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
cur.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end());//排序 用于去重
dfs(nums, used);
return result;
}
};
剑指 Offer 38. 字符串的排列
剑指 Offer 38. 字符串的排列

元素不能重复使用,包含重复字母,
且不能出现重复排列
思路:
这题思路完全和 47. 全排列 II 一样 只是将元素换成的char
注意:
不同的dfs开始位置,不影响最终结果,故dfs的外边不需要循环。
class Solution {
public:
string cur="";
vector<string> res;
void dfs(string s,vector<int> &visited){
//终止条件
if(cur.size()==s.size()){
res.push_back(cur);
return;
}
for(int i=0;i<s.size();i++){
//剪枝
if(i>0 && s[i]==s[i-1] && visited[i-1]==1)
continue;
visited[i]=1;
cur.push_back(s[i]);
dfs(s,visited);
cur.pop_back();
visited[i]=0;
}
}
vector<string> permutation(string s){
vector<int> visited(s.size(),0);
sort(s.begin(),s.end());//排序
dfs(s,visited);
return res;
}
};
39. 组合总和
39. 组合总和
 思路:
思路:
任意顺序,可以重复选择
因为最后要求和,为了方便找到所有元素,故将元素排列
注意:
元素可以重复使用!重复排列不行(这就需要给定搜索空间)!
class Solution {
public:
//全局变量
vector<vector <int>> res;
vector<int> cur;
void dfs(int index,int count,vector<int>& candidates, int target){
if(count==target){
res.push_back(cur);
return;
}
if(count>target){
return;
}
if(index==candidates.size()){
return;
}
for(int i=index;i<candidates.size();i++){
//可以重复使用 所以不需要visited
//剪枝
//为了去重 则需要加index(规定当前进行到哪个位置,下一轮的搜索空间(index,n))
//此题为无重复元素的数组 故这一句不是很重要
if(i>0 && candidates[i-1]==candidates[i]){
continue;
}
count+=candidates[i];
cur.push_back(candidates[i]);
//注意 元素可以重复使用 下一次的搜索空间 相同
//但是这样可以确保它不会往回搜索 导致重复排列
dfs(i,count,candidates,target);
count-=candidates[i];
cur.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
dfs(0,0,candidates,target);
return res;
}
};
dfs for写法
void dfs(int index,int count,vector<int>& candidates,int target){
if(count==target){
res.push_back(cur);
return;
}
for(int i=index;i<candidates.size();i++){
if(count>target)
continue;
cur.push_back(candidates[i]);
//注意 元素可以重复使用 因此下一次区间还是从i开始
dfs(i,count+candidates[i],candidates,target);//更新i和当前状态的sum
cur.pop_back();
}
}
40. 组合总和 II
40. 组合总和 II

元素不可以重复使用!重复排列不行(这就需要给定搜索空间)
class Solution {
public:
vector<int> cur;
vector<vector<int>> res;
void dfs(int index,int count,vector<int>& candidates, int target){
if(index==candidates.size() && count==target){
res.push_back(cur);
return;
}
if(count==target){
res.push_back(cur);
return;
}
if(count>target || index>=candidates.size()){
return;
}
for(int i=index;i<candidates.size();i++){
//剪枝 去重
if(i>index && candidates[i-1]==candidates[i]){
continue;
}
count+=candidates[i];
cur.push_back(candidates[i]);
dfs(i+1,count,candidates,target);
cur.pop_back();
count-=candidates[i];
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
//每个数只能用一次 这说明应该给定搜索空间
sort(candidates.begin(),candidates.end());
dfs(0,0,candidates,target);
return res;
}
};
78. 子集
78. 子集

思路:
这种和全排列的那种题目就不一样,它不要求全部要选到
因此到达终点的结束条件不能携程 cur.size()==nums.size()
每个元素 分为 选到 和 不选 两种状态
它的结束条件应该是判断是不是所有节点都处理过了,也就是说剩下的搜索空间为【index,n】
在index==n时,就可以返回
class Solution {
public:
//全局变量
vector<vector<int>> res;
vector<int> cur;
void dfs(int index,int n,vector<int>& nums){
if(index==n){
res.push_back(cur);
return;
}
//分为两种情况 直接写(可以不用for拓展)
//选中
cur.push_back(nums[index]);//修改状态
dfs(index+1,n,nums);
cur.pop_back();//恢复状态
//不选
//直接跳过 不需要改变状态
dfs(index+1,n,nums);
}
vector<vector<int>> subsets(vector<int>& nums){
//获得所有可行解 回溯法
int n=nums.size();
dfs(0,n,nums);
return res;
}
};
参考题解:
C++ 总结了回溯问题类型 带你搞懂回溯算法(大量例题)
for循环拓展的dfs
第一层for循环代表的递归树第一层,第二层for循环代表递归树第二层,以此类推。每层for循环里的做出选择与撤销选择,选择各自层的路径(第一层for循环选择第一层路径)

void dfs(int index,int n,vector<int>& nums){
res.push_back(cur);
for(int i=index;i<nums.size();i++){
cur.push_back(nums[i]);
dfs(i+1,n,nums);
cur.pop_back();
}
}
90. 子集 II
思路:
加一个剪枝操作
class Solution {
public:
//全局变量
vector<vector<int>> res;
vector<int> cur;
void dfs(int index,vector<int>& nums){
//结束条件
res.push_back(cur);
for(int i=index;i<nums.size();i++){
//剪枝
if(i>index && nums[i-1]==nums[i]){
continue;
}
cur.push_back(nums[i]);
dfs(i+1,nums);
cur.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
//包含重复元素 先排序
sort(nums.begin(),nums.end());
dfs(0,nums);
return res;
}
};
473. 火柴拼正方形
473. 火柴拼正方形
2022年61儿童节(每日一题杀我)
思路:(参考官方题解)
首先计算所有火柴的总长度 totalLen,如果 totalLen 不是 4 的倍数,那么不可能拼成正方形,返回 false。当 totalLen 是 4的倍数时,每条边的边长为len = totalLen\4
用edges 来记录 4 条边已经放入的火柴总长度。
对于第index根火柴,尝试把它放入其中一条边内且满足放入后该边的火柴总长度不超过len,然后继续枚举第 index+1 根火柴的放置情况,如果所有火柴都已经被放置,那么说明可以拼成正方形。
为了减少搜索量,需要对火柴长度从大到小进行排序。
class Solution {
public:
bool dfs(int index, vector<int>& matchsticks, vector<int>& edges,int len){
//搜索完全部火柴,放入桶中
if(index==matchsticks.size()){
return true;
}
//拓展情况
//尝试把火柴放入4个桶中(edges)
for(int i=0; i<edges.size();i++){
if(matchsticks[index]+edges[i]<=len){//只有在桶容量足够时才能放入
edges[i]+=matchsticks[index];//修改状态
if(dfs(index+1,matchsticks,edges,len))
return true;
edges[i]-=matchsticks[index];//恢复状态
}
if (matchsticks[index]+edges[i]>len)
continue;
}
return false;
}
bool makesquare(vector<int> &matchsticks) {
int totalLen = accumulate(matchsticks.begin(), matchsticks.end(), 0);
if(totalLen % 4 != 0){
return false;
}
sort(matchsticks.begin(), matchsticks.end(), greater<int>()); // 减少搜索量
vector<int> edges(4);
return dfs(0, matchsticks, edges, totalLen/4);
}
};
元素不能重复使用,包含重复元素=>直接给定搜索空间
剪枝优化:
bool dfs(int index, vector<int>& matchsticks, vector<int>& edges,int len){
//搜索完全部火柴,放入桶中
if(index==matchsticks.size()){
return true;
}
//拓展情况
//尝试把火柴放入4个桶中(edges)
for(int i=0; i<edges.size();i++){
if(matchsticks[index]+edges[i]<=len){//只有在桶容量足够时才能放入
//剪枝
if(i>index && matchsticks[i-1]==matchsticks[i]){
continue;
}
edges[i]+=matchsticks[index];//修改状态
if(dfs(index+1,matchsticks,edges,len))
return true;
edges[i]-=matchsticks[index];//恢复状态
}
if (matchsticks[index]+edges[i]>len)
continue;
}
return false;
}
(二)二维数组/字符串
79. 单词搜索
79. 单词搜索

思路:
这题就是 地图型,根据题意,搜索的元素未相邻的元素
注意 要求搜索到的元素必须有序 因此需要使用 index
结束条件:搜索到完整的单词
注意到:不同的dfs开始的位置=》最终的结果不同(按顺序)
故dfs的外边需要 循环,来判断dfs从哪个位置开始(有意义)。
并且,只要找到一个可行解即可返回。
index:我们注意到,进行下一步时都是index+1,这说明前【0,index】个位置的状态(我们已经做的选择、标记)已经固定。
故最终的结束条件为index==word.size(),前【0,n】已经做好,已经搜索到长度为n的单词。
class Solution {
public:
bool dfs(int x,int y,int index,vector<vector<char>>& board,string word,vector<vector<int>> &visited){
//结束条件
if(index==word.size()){
return true;
}
//边界
if(x<0||y<0||x>=board.size()||y>=board[0].size()){
return false;
}
//剪枝
if (word[index] != board[x][y] || visited[x][y]==1) {
return false;
}
bool ans=false;
visited[x][y] = 1; //标记
//可走的有四个方向
ans=dfs(x+1,y,index+1,board,word,visited)||
dfs(x-1,y,index+1,board,word,visited)||
dfs(x,y+1,index+1,board,word,visited)||
dfs(x,y-1,index+1,board,word,visited);
visited[x][y]=0;//恢复标记
return ans;
}
bool exist(vector<vector<char>>& board, string word) {
//像这种按顺序匹配的,要用到index
//因为同一个单元格的元素不能重复使用 故需要一个访问数组
vector<vector<int>> visited(board.size(),vector<int>(board[0].size(),0));
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[i].size(); j++) {
if (board[i][j] == word[0]) {
if (dfs(i,j,0,board,word,visited))
return true;
}
}
}
return false;
}
};
也可以把可拓展的、可走的位置(方向)罗列出来,这样用for循环,更加直观。
同时,剪枝位置可以在dfs的一开始,也可以在for循环要走的位置开始。
就是说:
(1)走了再判断能不能走,不能走直接返回;
(2)走之前就判断能不能走,不能走就直接跳过;
//下一步可以走的位置 四个方向
vector<pair<int, int>> next{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
bool dfs(int i,int j,int index,int m,int n,string word,vector<vector<char>> board,vector<vector<int>>& visited){
if(board[i][j] != word[index]){
return false;
}
else if(index == word.size()-1){//所有元素都有出现过
return true;
}
bool result = false;
visited[i][j]=1;//访问该节点
for (const auto& dir: next) {//四个方向
int newi = i + dir.first;
int newj = j + dir.second;
if (newi >= 0 && newi < board.size() && newj >= 0 && newj < board[0].size()) {//防止越界
if (!visited[newi][newj]) {
bool flag = dfs(newi, newj,index+1,m,n,word,board,visited);
if (flag) {//如果已经走到终点,发现有可以走的路径
result = true;
break;
}
}
}
}
visited[i][j]=0;//回退状态
return result;
}
bool exist(vector<vector<char>>& board, string word) {
int m=board.size();
int n=board[0].size();
vector<vector<int>> visited(m,vector<int>(n,0));
// vector show(word.size(),0);
// 不需要额外加一个数组存储状态
// 因为回溯法需要连续遍历每一个能走的位置 因此只需要将回溯法的返回值定义为bool
// 即可知道这一步是不是可以的
// 需要加一个index去判断 word[index]是否为真
// 而且 回溯法从哪个位置开始走也很重要
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
bool flag = dfs(i, j, 0,m, n, word, board, visited);
if (flag) {
return true;
}
}
}
return false;
}
62. 不同路径
class Solution {
public:
int res=0;
void dfs(int i,int j,int m,int n,vector<vector<int>> &visited){
//结束条件
if(i==m-1 && j==n-1){
res+=1;
return;
}
// 存在的位置都可访问,因此不需要判断合法
visited[i][j]=1;
//扩展方式
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i+1<m)
dfs(i+1,j,m,n,visited);
if(j+1<n)
dfs(i,j+1,m,n,visited);
}
}
}
int uniquePaths(int m, int n) {
//如果是最小路径 那就是dp
//如果是不同路径 那就是回溯法 dfs
vector<vector<int>> visited(m,vector<int>(n,0));
dfs(0,0,m,n,visited);
return res;
}
};
dp做法:请移步我动态规划的博客: leetcode_刷题总结(c++)_动态规划
51. N 皇后
51. N 皇后


思路:
使用标记数组,将不能访问的位置标记上。
皇后们的约束条件:
- 不能同行 (因为递归进去是row+1,默认每行只能填充一个值,故不需要再设置标记数组)
- 不能同列 (标记数组column;一列)
- 不能同斜线(标记数组 rboard、lboard ;正对角线和负对角线)
判断是否在同一斜线:(参考官方题解)
同一主对角线:(row-col)相同===》(n-1)-(row-col)=》n-1-row+col (保证不为负数,数组下标有意义)

同一副对角线:(row+col) 相同

写法一(标记数组写法):
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> ans;
vector<string> board(n,string(n,'.'));
vector<bool> column(n,false); //同一列是否使用
vector<bool> rboard(2*n-1,false);//同斜线是否使用
vector<bool> lboard(2*n-1,false);//同斜线是否使用
backtrace(ans,board,column,lboard,rboard,0,n);
return ans;
}
void backtrace(vector<vector<string>>& ans,vector<string>& board,vector<bool>& column,vector<bool>& lboard,vector<bool>& rboard,int row,int n){
//结束条件 (0,n)行的左右位置都填好了 row相当于index
if(row == n){
ans.push_back(board);
return;
}
for(int col=0;col<n;col++){//拓展 将这一行填完
if(column[col]||rboard[row+col]||lboard[n-1-row+col]){
continue;
}
//修改状态
column[col]=rboard[row+col]=lboard[n-1-row+col]=true;
board[row][col]='Q';
//递归入口
backtrace(ans,board,column,lboard,rboard,row+1,n);
//恢复状态
column[col]=rboard[row+col]=lboard[n-1-row+col]=false;
board[row][col]='.';
}
}
};
写法二(哈希表写法):
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
auto solutions = vector<vector<string>>();
auto queens = vector<int>(n, -1); //同一行
auto columns = unordered_set<int>(); //同一列
auto diagonals1 = unordered_set<int>(); //同一对角线
auto diagonals2 = unordered_set<int>(); //同一对角线
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
//结束条件 (0,n)行的左右位置都填好了
if (row == n) {
vector<string> board = generateBoard(queens, n);
solutions.push_back(board);
} else {
// 扩展情况
for (int i = 0; i < n; i++) {// i是在列方向上尝试填充
// 判断同一列是否使用
if (columns.find(i) != columns.end()) {
continue;
}
// 判断同一对角线是否使用
int diagonal1 = row - i;
if (diagonals1.find(diagonal1) != diagonals1.end()) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.find(diagonal2) != diagonals2.end()) {
continue;
}
//修改状态
queens[row] = i;
columns.insert(i);
diagonals1.insert(diagonal1);
diagonals2.insert(diagonal2);
//递归入口
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
//恢复状态
queens[row] = -1;
columns.erase(i);
diagonals1.erase(diagonal1);
diagonals2.erase(diagonal2);
}
}
}
vector<string> generateBoard(vector<int> &queens, int n) {
auto board = vector<string>();
for (int i = 0; i < n; i++) {
string row = string(n, '.');
row[queens[i]] = 'Q';
board.push_back(row);
}
return board;
}
};
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/n-queens/solution/nhuang-hou-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
37. 解数独
37. 解数独


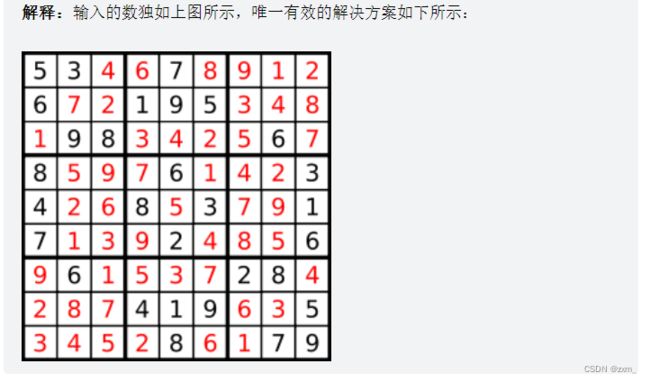
思路:
与N皇后类似,设计标记数组来限制重复填写。
数独的解法约束:
- 数字 1-9 在每一行只能出现一次。 x_uesd[row][num]=true 即 第row行已经填写num数字
- 数字 1-9 在每一列只能出现一次。 y_uesd[col][num]
- 数字 1-9 在每一个以粗实线分隔的 3x3宫内只能出现一次。sub_uesd[index][num]
x_uesd[row][num]=true 即 第row行已经填写num数字
y_uesd[col][num]=true 即 第col列已经填写num数字
sub_uesd[index][num]=true 即 第index宫已经填写num数字
using namespace std;
class Solution {
public:
vector<vector<char>> res;
bool x_uesd[9][9];
bool x_uesd[9][9];
bool sub_uesd[9][9];
vector<pair<int, int>> mSpace;//需要填充的位置
bool dfs(int index, vector<vector<char>>& board){
if (index == mSpace.size()) {//需要填充的位置都填完了
return true;
}
auto x = mSpace[index].first;
auto y = mSpace[index].second;
//扩展 可以填的有9个数
for (auto c = '1'; c <= '9'; c++) {
auto num = c - '1';
//符合条件的数可以填入
if (!x_uesd[x][num] && !y_uesd[y][num] && !sub_uesd[x / 3 * 3 + y / 3][num]){
//修改状态
board[x][y] = c;
x_uesd[x][num] = true;
y_uesd[y][num] = true;
sub_uesd[x / 3 * 3 + y / 3][num] = true;
//递归
if (dfs(index + 1,board)){
return true;
}
//恢复状态
x_uesd[x][num] = false;
y_uesd[y][num] = false;
sub_uesd[x / 3 * 3 + y / 3][num] = false;
}
}
return false;
}
void solveSudoku(vector<vector<char>>& board) {
//固定长度大小为9*9
//保证只有一个解 回溯法找到答案即可返回
//因此dfs可以设置为bool型
//初始化
for (auto i=0;i<board.size();i++){
for (auto j=0;j<board[i].size();j++){
char c = board[i][j];
if (c == '.') {//未填写:需要填充的位置
mSpace.emplace_back(i, j);
}
else {//已填写:修改标记数组
//从0开始 因此直接-'1'
x_uesd[i][c - '1'] = true;
y_uesd[j][c - '1'] = true;
sub_uesd[i / 3 * 3 + j / 3][c - '1'] = true;
}
}
}
dfs(0,board);
}
};
(三)其他
22. 括号生成
22. 括号生成

思路:
像这种 给出所有组合,一般都能用回溯法做出
注意:
要的是 有效的括号组合
class Solution {
public:
//全局变量
vector<string> res;
string cur="";
void dfs(int leftcount,int rightcount,int n){
//因为括号有分左右括号 因此结束条件为 2*n
if(cur.size()==2*n && leftcount==rightcount){
res.push_back(cur);
}
//是否需要用到堆栈
//如果不使用堆栈 则需要记录当前 左括号个数 以及 右括号个数
//在有效情况下,左括号个数>右括号个数
//剪枝
if(leftcount<rightcount || leftcount>n || rightcount>n || leftcount+rightcount>2*n){
return;
}
//每次只有两种情况 进左括号 or 进右括号
//因此可以不用for 直接写
//第一种 进左括号
cur.push_back('(');
dfs(leftcount+1,rightcount,n);
cur.pop_back();//还原
//第二种 进右括号
cur.push_back(')');
dfs(leftcount,rightcount+1,n);
cur.pop_back();//还原
}
vector<string> generateParenthesis(int n){
dfs(0,0,n);
return res;
}
};




