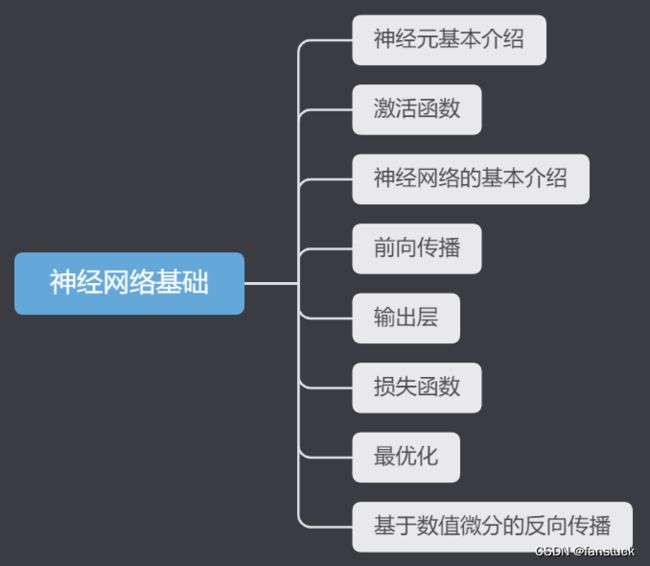
一文速学-让神经网络不再神秘，一天速学神经网络基础(六)-基于数值微分的反向传播

---

前言

思索了很久到底要不要出深度学习内容，毕竟在数学建模专栏里边的机器学习内容还有一大半算法没有更新，很多坑都没有填满，而且现在深度学习的文章和学习课程都十分的多，我考虑了很久决定还是得出神经网络系列文章，不然如果以后数学建模竞赛或者是其他更优化模型如果用上了神经网络（比如利用LSTM进行时间序列模型预测），那么就更好向大家解释并且阐述原理了。但是深度学习的内容不是那么好掌握的，包含大量的数学理论知识以及大量的计算公式原理需要推理。且如果不进行实际操作很难够理解我们写的代码究极在神经网络计算框架中代表什么作用。不过我会尽可能将知识简化，转换为我们比较熟悉的内容，我将尽力让大家了解并熟悉神经网络框架，保证能够理解通畅以及推演顺利的条件之下，尽量不使用过多的数学公式和专业理论知识。以一篇文章快速了解并实现该算法，以效率最高的方式熟练这些知识。

现在很多竞赛虽然没有限定使用算法框架，但是更多获奖的队伍都使用到了深度学习算法，传统机器学习算法日渐式微。比如2022美国大学生数学建模C题，参数队伍使用到了深度学习网络的队伍，获奖比例都非常高，现在人工智能比赛和数据挖掘比赛都相继增多，对神经网络知识需求也日渐增多，因此十分有必要掌握各类神经网络算法。

博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。

本篇文章为神经网络基础的最后一章了也是最关键的一章，至此整个神经网络的基础架构和每个节点的功能基本都跃然纸上，个人认为还是比较清楚详细的。根据前面五篇文章的基础，我们已经可以构造出一个基础的初级神经网络，但是蕴含神经网络最灵魂的关键步骤-反向传播还没有展开讲述，本篇文章将通过梯度下降最优化算法的神经网络对手写数字识别。

---

基于数值微分的反向传播

激活函数

根据我们学习的步骤来，先将工具写好，也就是激活函数。我们明确目标就是要对手写数字识别项目，我们最后需要对识别的图片进行分类，自然想到了Softmax激活函数，既然是搭深度学习的网络少不了的是ReLu大家族，我们先把这两个工具写上：

#启发函数(激活函数)ReLU
def _relu(in_data):
    return np.maximum(0,in_data)

#激活函数Softmax
def _softmax(x):
    if x.ndim == 2:
        c = np.max(x,axis=1)
        x = x.T - c #溢出对策
        y = np.exp(x) / np.sum(np.exp(x),axis=0)
        return y.T
    c = np.max(x)
    exp_x = np.exp(x-c)
    return exp_x/np.sum(exp_x)

 损失函数

损失函数的话，上次数值微分已经有讲过了，诸如此类图像分类一般使用交叉熵损失函数（Cross Entropy Loss），交叉熵损失函数是用于度量分类问题中预测值与真实标签之间的差距，它在深度学习中得到了广泛的应用。交叉熵损失函数在多分类问题中的表现非常好，比如在图像分类、自然语言处理等领域。如果对损失函数认识的还不是足够了解的话，推荐大家看看我的这篇文章：

损失函数(Loss Function)一文详解-分类问题常见损失函数Python代码实现+计算原理解析

直接给出代码：

#损失函数
def cross_entropy_error(p,y):
    delta =1e-7
    batch_size = p.shape[0]
    return -np.sum(y*np.log(p+delta))/batch_size

比较简单实现。

数值微分

数值微分的概念之前讲述的并不是很详细这里补充一下。数值微分是一种计算导数（或斜率）的数值近似方法。导数是函数在某一点上的变化率，它告诉我们函数在该点上的输出值对输入值的响应程度。数值微分允许我们通过在某一点附近的小范围内取函数值来估计导数。常用的方法有两种：

前向差分（Forward Difference）： 前向差分通过计算函数在某一点处的值和稍后一个点处的值之间的差异来估计导数。前向差分的数值微分公式：

其中，是一个小的正数，称为微分步长。通过选择不同的微分步长，可以获得不同精度的估计。.

中心差分（Central Difference）： 中心差分通过计算函数在某一点处的值和点和处的值之间的差异来估计导数。中心差分的数值微分公式：

中心差分通常比前向差分更精确，因为它考虑了点周围的函数值。

数值微分的主要应用是在没有解析导数表达式的情况下，计算函数的导数。它在数值优化、数值积分、机器学习中的梯度计算以及其他涉及导数的数值方法中都有广泛的应用。

需要注意的是，数值微分是一种数值近似方法，其精度受到微分步长的影响。较小的微分步长通常会导致更准确的估计，但也可能引入数值稳定性问题。因此，在实际应用中，需要根据具体问题和计算资源来选择合适的微分步长。

Python计算实现方法为：

def numerical_gradient(f,x):
    h = 1e-4 #0.0001
    grad = np.zeros_like(x)
    it = np.nditer(x,flags=['multi_index'],op_flags=['readwrite'])
    while not it.multi_index:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val)+h
        fxh1 = f(x) #f(x+h)
        
        x[idx] = tmp_val-h
        fxh2 = f(x) #f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val #还原值
        it.iternext()
        
    return grad

 定义神经网络

接下来搭建我们自己的神经网络了，按照步骤来保证我们不会遗忘关键点，之前以及在上篇文章前向传播中详细讲述的网络的搭建过程，有遗忘的小伙伴推荐再去看看几遍，想要一遍记住神经网络结构和搭建还是挺难的，首先我们需要初始化我们的网络：

class TwoLayerNet:
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        #初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size,hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size,output_size)
        self.params['b2'] = np.zeros(output_size)
        

 设置好权重和隐藏层，其中W1的形状是(input_size,hidden_size),W2的形状是(hidden_size,output_size)。接着就是前向传播，把网络功能完善好。

前向传播

推荐大家再看一遍前向传播帮助自己记忆：一文速学-让神经网络不再神秘，一天速学神经网络基础-前向传播（三）

 这里不再过多描述，实现方法：

def predict(self,x):
        W1,W2 = self.params['W1'],self.params['W2']
        b1,b2 = self.params['b1'],self.params['b2']

        a1 = np.dot(x,W1)+b1
        z1 = _relu(a1)
        a2 = np.dot(z1,W2)+b2
        p = _softmax(a2)

 现在来计算损失值，对于预测值来说，其结果就是通过前向传播计算得到，之后调用函数cross_entropy_error,得到损失函数的损失值Loss，我们的目标就是使得Loss不断减少：

#x:输入数据，y:监督数据
    def loss(self,x,y):
        p = self.predict(x)

        return cross_entropy_error(p,y)

 然后根据损失值来计算推理，得到最优权重集，目标十分明确。

最优化

我们采取的是计算梯度下降最优化的算法：

#x:输入数据，y:监督数据
    def numerical_gradient(self,x,y):
        loss_W = lambda W:self.loss(x,y)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W,self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W,self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W,self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W,self.params['b2'])
        
        return grads

 模型检测

计算模型指标的算法有很多种，一般来说此类分类算法检测常用的指标有三个，当然在我之前的文章也有详细介绍过，而且也有可视化展示十分好用，推荐大家阅读一下：

sklearn预测评估指标计算详解：准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1score

这里用一个AC方便展示：

def accuracy(self,x,t):
        p = self.predict(x)
        p = np.argmax(p,axis=1)
        y = np.argmax(t,axis=1)

        accuracy = np.sum(p == y)/float(x.shape[0])
        return accuracy

 好了基本的轮子也搭建好了，接下来我们就开始让代码运行起来：

#超参数
iters_num = 1000 #适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.001

network = TwoLayerNet(input_size = 784,hidden_size=50,output_size=10)
for i in range(iters_num):
    batch_mask = np.random.choice(train_size,batch_size)
    x_batch = x_train[batch_mask]
    y_batch = y_train[batch_mask]
    
    grad = network.numerical_gradient(x_batch,y_batch)
    
    for key in ('W1','b1','W2','b2'):
        network.params[key] -= learning_rate*grad[key]
#记录学习过程
    loss =network.loss(x_batch,y_batch)
    print(loss)

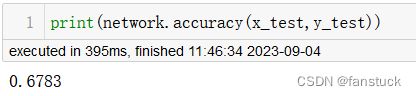
我这里训练了几十个循环准确率可以达到67%：

那么本篇文章到这里就告一段落了，至此我们以及把整个神经网络的框架搭完了，很多可以细化需要填充的东西我们放到以后再讲，各位学习到这里已经具备搭建初级神经网络的能力，可以去跑一些其他传统的机器学习项目看看效果，那么下一章我们再去了解一下神经网络的多次epoch训练。

---