深入理解线段树
大家好,我是 方圆。线段树(Segment Tree) 是常用的维护 区间信息 的数据结构,它可以在 O(logn) 的时间复杂度下实现单点修改、区间修改、区间查询(区间求和、区间最大值或区间最小值)等操作,常用来解决 RMQ 问题。
RMQ(Range Minimum/Maximum Query) 问题是指:对于长度为 n 的数列 A,回答若干询问 RMQ(A, i, j) 其中 i, j <= n,返回数列 A 中下标在 i, j 里的最小(大)值。也就是说:RMQ问题是指求区间最值的问题。通常该类型题目的解法有 递归分治、动态规划、线段树 和 单调栈/单调队列。
本文我们将介绍线段树并在后文添加相关题目进行练习。这篇内容断断续续写了两周,随着练习对线段树的理解不断深入,慢慢地学习下来也不觉得它有多么困难,更多的体会还是熟能生巧,虽然它起初看上去确实代码量大一些,但是我觉得只要大家放平心态,循序渐进的掌握下文中的三部分,也没什么难的。如果大家想要找刷题路线的话,可以参考 Github: LeetCode。
1. 线段树
线段树会将每个长度不为 1 的区间划分成左右两个区间来递归求解,通过合并左右两区间的信息来求得当前区间的信息。
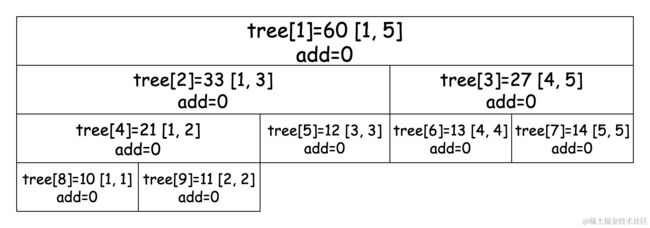
比如,我们将一个大小为 5 的数组 nums = {10, 11, 12, 13, 14} 转换成线段树,并规定线段树的根节点编号为 1。用数组 tree[] 来保存线段树的节点,tree[i] 表示线段树上编号为 i 的节点,图示如下:
图示中每个节点展示了区间和以及区间范围,tree[i] 左子树节点为 tree[2i],右子树节点为 tree[2i + 1]。如果 tree[i] 记录的区间为 [a, b] 的话,那么左子树节点记录的区间为 [a, mid],右子树节点记录的区间为 [mid + 1, b],其中 mid = (a + b) / 2。
现在我们已经对线段树有了基本的认识,接下来我们看看 区间查询和单点修改 的代码实现。
区间查询和单点修改线段树
首先,我们定义线段树的节点:
/**
* 定义线段树节点
*/
class Node {
/**
* 区间和 或 区间最大/最小值
*/
int val;
int left;
int right;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
注意其中的 val 字段保存的是区间的和。定义完树的节点,我们来看一下建树的逻辑,注意代码中的注释,我们为线段树分配的节点数组大小为原数组大小的 4 倍,这是考虑到数组转换成满二叉树的最坏情况。
public SegmentTree(int[] nums) {
this.nums = nums;
tree = new Node[nums.length * 4];
// 建树,注意表示区间时使用的是从 1 开始的索引值
build(1, 1, nums.length);
}
/**
* 建树
*
* @param pos 当前节点编号
* @param left 当前节点区间下界
* @param right 当前节点区间上界
*/
private void build(int pos, int left, int right) {
// 创建节点
tree[pos] = new Node(left, right);
// 递归结束条件
if (left == right) {
// 赋值
tree[pos].val = nums[left - 1];
return;
}
// 如果没有到根节点,则继续递归
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 当前节点的值是左子树和右子树节点的和
pushUp(pos);
}
/**
* 用于向上回溯时修改父节点的值
*/
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
我们在建树时,表示区间并不是从索引 0 开始,而是从索引 1 开始,这样才能保证在计算左子树节点索引时为 2i,右子树节点索引为 2i + 1。
build() 方法执行时,我们会先在对应的位置上创建节点而不进行赋值,只有在递归到叶子节点时才赋值,此时区间大小为 1,节点值即为当前区间的值。之后非叶子节点值都是通过 pushUp() 方法回溯加和当前节点的两个子节点值得出来的。
接下来我们看修改区间中的值,线段树对值的更新方法,关注其中的注释:
/**
* 修改单节点的值
*
* @param pos 当前节点编号
* @param numPos 需要修改的区间中值的位置
* @param val 修改后的值
*/
private void update(int pos, int numPos, int val) {
// 找到该数值所在线段树中的叶子节点
if (tree[pos].left == numPos && tree[pos].right == numPos) {
tree[pos].val = val;
return;
}
// 如果不是当前节点那么需要判断是去左或右去找
int mid = tree[pos].left + tree[pos].right >> 1;
if (numPos <= mid) {
update(pos << 1, numPos, val);
} else {
update(pos << 1 | 1, numPos, val);
}
// 叶子节点的值修改完了,需要回溯更新所有相关父节点的值
pushUp(pos);
}
修改方法比较简单,当叶子节点值更新完毕时,我们仍然需要调用 pushUp() 方法对所有相关父节点值进行更新。
接下来我们看查找对应区间和的方法:
/**
* 查找对应区间的值
*
* @param pos 当前节点
* @param left 要查询的区间的下界
* @param right 要查询的区间的上界
*/
private int query(int pos, int left, int right) {
// 如果我们要查找的区间把当前节点区间全部包含起来
if (left <= tree[pos].left && tree[pos].right <= right) {
return tree[pos].val;
}
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
// 根据区间范围去左右节点分别查找求和
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
该方法也比较简单,需要判断区间范围是否需要对向左子节点和右子节点的分别查找计算。
现在表示区间和的线段树已经讲解完毕了,为了方便大家学习和看代码,我把全量的代码在这里贴出来:
public class SegmentTree {
/**
* 定义线段树节点
*/
static class Node {
/**
* 区间和 或 区间最大/最小值
*/
int val;
int left;
int right;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
Node[] tree;
int[] nums;
public SegmentTree(int[] nums) {
this.nums = nums;
tree = new Node[nums.length * 4];
// 建树,注意表示区间时使用的是从 1 开始的索引值
build(1, 1, nums.length);
}
/**
* 建树
*
* @param pos 当前节点编号
* @param left 当前节点区间下界
* @param right 当前节点区间上界
*/
private void build(int pos, int left, int right) {
// 创建节点
tree[pos] = new Node(left, right);
// 递归结束条件
if (left == right) {
// 赋值
tree[pos].val = nums[left - 1];
return;
}
// 如果没有到根节点,则继续递归
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 当前节点的值是左子树和右子树节点的和
pushUp(pos);
}
/**
* 修改单节点的值
*
* @param pos 当前节点编号
* @param numPos 需要修改的区间中值的位置
* @param val 修改后的值
*/
private void update(int pos, int numPos, int val) {
// 找到该数值所在线段树种的叶子节点
if (tree[pos].left == numPos && tree[pos].right == numPos) {
tree[pos].val = val;
return;
}
// 如果不是当前节点那么需要判断是去左或右去找
int mid = tree[pos].left + tree[pos].right >> 1;
if (numPos <= mid) {
update(pos << 1, numPos, val);
} else {
update(pos << 1 | 1, numPos, val);
}
// 叶子节点的值修改完了,需要回溯更新所有相关父节点的值
pushUp(pos);
}
/**
* 用于向上回溯时修改父节点的值
*/
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
/**
* 查找对应区间的值
*
* @param pos 当前节点
* @param left 要查询的区间的下界
* @param right 要查询的区间的上界
*/
private int query(int pos, int left, int right) {
// 如果我们要查找的区间把当前节点区间全部包含起来
if (left <= tree[pos].left && tree[pos].right <= right) {
return tree[pos].val;
}
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
// 根据区间范围去左右节点分别查找求和
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
}
如果要创建表示区间最大值或最小值的线段树,建树的逻辑不变,只需要将 pushUp() 方法和 query() 方法修改成计算最大值或最小值的逻辑即可。
相关题目
- 307. 区域和检索 - 数组可修改
区域和的检索是一道中等难度的题目,属于典型的 RMQ 问题,根据题目要求,我们可以直接将线段树模板写下来即可。
- 239. 滑动窗口最大值
该题在 Leetcode 上是困难的题目,根据题目要求,需要在数组的子区间内取最大值,这也是 RMQ 问题,很容易想到线段树的解法。它与我们上述线段树模板不同的地方是:模板中是区间求和,而题目要求区间最大值,我们只需要将模版中 pushUp() 方法和 query() 方法改成求最大值即可,如下:
private void pushUp(int pos) {
// 取左右子树的大值
tree[pos].val = Math.max(tree[pos << 1].val, tree[pos << 1 | 1].val);
}
private int query(int pos, int left, int right) {
if (left <= tree[pos].left && tree[pos].right <= right) {
return tree[pos].val;
}
int res = Integer.MIN_VALUE;
int mid = tree[pos].left + tree[pos].right >> 1;
if (left <= mid) {
res = Math.max(res, query(pos << 1, left, right));
}
if (right > mid) {
res = Math.max(res, query(pos << 1 | 1, left, right));
}
return res;
}
- 654. 最大二叉树
本题目依然是求解区间内的最大值并构建二叉树,解法与上一题类似,不同的是本题我们不光要记录区间内最大值,也要把该最大值的在区间中的索引记录下来,因为需要依靠索引值来递归创建二叉树。
2. 线段树的区间修改与懒惰标记
如果我们不仅对单点进行修改,也对区间进行修改,那么在区间修改时就需要将当前区间值及包含当前区间的子区间值都修改一遍,这样所产生的开销是没办法接受的,因此在这里我们会使用一种 懒惰标记 的方法来帮助我们 避免这种即时开销。
简单来说,懒惰标记是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次 “即将访问(update 或 query)”到带有懒惰标记节点的子节点 时才进行。
我们通过在节点类中添加 add 字段记录懒惰标记,它表示的是该区间的子区间值需要“变化的大小”(一定好好好的理解),并通过 pushDown 方法“累加”到当前区间的两个子节点区间值中。
只要不访问到当前区间的子区间,那么子区间值始终都不会变化,相当于子区间值的变化量被当前节点通过 add 字段“持有”
pushDown 方法区别于我们上文中提到的 pushUp 方法,前者是将当前节点值累计的懒惰标记值同步到子节点中,而后者是完成子节点修改后,回溯修改当前子节点的父节点值,我们能够根据 Down 和 Up 来更好的理解这两个方法的作用方向和修改范围。
下面我们一起来看看过程和具体的代码,节点类如下,增加 add 字段:
static class Node {
int left;
int right;
int val;
int add;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
区间修改
建树的流程与我们上述的一致,就不在这里赘述了,我们主要关注区间修改的过程,还是以如下初始的线段树为例,此时各个节点的 add 均为 0:
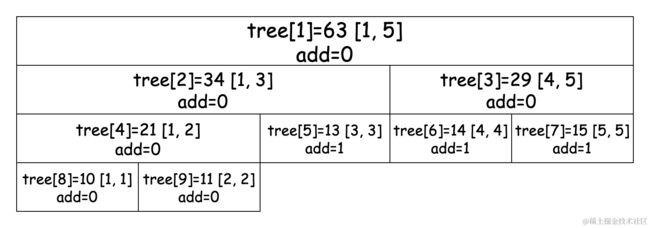
接下来我们修改区间 [3, 5] 且区间内 每个值变化量为 1,过程如下:
先遍历节点 1,发现 [3, 5] 区间不能将 [1, 5] 区间 完全包含,不进行修改,继续遍历节点 2。节点 2 依然没有被区间 [3, 5] 包含,需要继续遍历节点 5,发现该节点被区间完全包含,进行修改并添加懒惰标记值,如下图所示:
完成这一步骤后需要向上回溯修改 tree[2] 节点的值:
现在 [3, 5] 区间中 3 已经完成修改,还有 4, 5 没有被修改,我们需要在右子树中继续递归查找,发现 tree[3] 中区间被我们要修改的区间 [3, 5] 完全包含,那么需要将这个节点进行修改并懒惰标记,如下,注意这里虽然 tree[3] 节点有两个子节点,但是因为我们没有访问到它的子节点所以无需同步 add 值到各个子节点中:
同样,完成这一步骤也需要向上回溯修改父节点的值:
到现在我们的区间修改就已经完成了,根据这个过程代码示例如下:
/**
* 修改区间的值
*
* @param pos 当前节点编号
* @param left 要修改区间的下界
* @param right 要修改区间的上界
* @param val 区间内每个值的变化量
*/
public void update(int pos, int left, int right, int val) {
// 如果该区间被要修改的区间包围的话,那么需要将该区间所有的值都修改
if (left <= tree[pos].left && tree[pos].right <= right) {
tree[pos].val += (tree[pos].right - tree[pos].left + 1) * val;
// 懒惰标记
tree[pos].add += val;
return;
}
// 该区间没有被包围的话,需要修改节点的信息
pushDown(pos);
int mid = tree[pos].left + tree[pos].right >> 1;
// 如果下界在 mid 左边,那么左子树需要修改
if (left <= mid) {
update(pos << 1, left, right, val);
}
// 如果上界在 mid 右边,那么右子树也需要修改
if (right > mid) {
update(pos << 1 | 1, left, right, val);
}
// 修改完成后向上回溯修改父节点的值
pushUp(pos);
}
private void pushDown(int pos) {
// 根节点 和 懒惰标记为 0 的情况不需要再向下遍历
if (tree[pos].left != tree[pos].right && tree[pos].add != 0) {
int add = tree[pos].add;
// 计算累加变化量
tree[pos << 1].val += add * (tree[pos << 1].right - tree[pos << 1].left + 1);
tree[pos << 1 | 1].val += add * (tree[pos << 1 | 1].right - tree[pos << 1 | 1].left + 1);
// 子节点懒惰标记累加
tree[pos << 1].add += add;
tree[pos << 1 | 1].add += add;
// 懒惰标记清 0
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
区间查询
tree[3] 节点是有懒惰标记 1 的,如果我们此时查询区间 [5, 5] 的值,就需要在递归经过 tree[3] 节点时,进行 pushDown 懒惰标记计算,将 tree[6] 和 tree[7] 的节点值进行修改,结果如下:
最终我们会获取到结果值为 15,区间查询过程的示例代码如下:
public int query(int pos, int left, int right) {
if (left <= tree[pos].left && tree[pos].right <= right) {
// 当前区间被包围
return tree[pos].val;
}
// 懒惰标记需要下传修改子节点的值
pushDown(pos);
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
同样,为了方便大家学习,我把全量代码也列出来,我认为学习线段树的区间修改比较重要的点是理解 add 字段表示的含义和 pushDown 方法的作用时机,而且需要注意只有 线段树中的某个区间被我们要修改的区间全部包含时(update 和 query 方法的条件判断),才进行值修改并懒惰标记,否则该区间值只在 pushUp 方法回溯时被修改。
public class SegmentTree2 {
static class Node {
int left;
int right;
int val;
int add;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
Node[] tree;
int[] nums;
public SegmentTree2(int[] nums) {
this.tree = new Node[nums.length * 4];
this.nums = nums;
build(1, 1, nums.length);
}
private void build(int pos, int left, int right) {
tree[pos] = new Node(left, right);
// 递归结束条件
if (left == right) {
tree[pos].val = nums[left - 1];
return;
}
int mid = left + right >> 1;
build(pos << 1, left, mid);
build(pos << 1 | 1, mid + 1, right);
// 回溯修改父节点的值
pushUp(pos);
}
/**
* 修改区间的值
*
* @param pos 当前节点编号
* @param left 要修改区间的下界
* @param right 要修改区间的上界
* @param val 区间内每个值的变化量
*/
public void update(int pos, int left, int right, int val) {
// 如果该区间被要修改的区间包围的话,那么需要将该区间所有的值都修改
if (left <= tree[pos].left && tree[pos].right <= right) {
tree[pos].val += (tree[pos].right - tree[pos].left + 1) * val;
// 懒惰标记
tree[pos].add += val;
return;
}
// 该区间没有被包围的话,需要修改节点的信息
pushDown(pos);
int mid = tree[pos].left + tree[pos].right >> 1;
// 如果下界在 mid 左边,那么左子树需要修改
if (left <= mid) {
update(pos << 1, left, right, val);
}
// 如果上界在 mid 右边,那么右子树也需要修改
if (right > mid) {
update(pos << 1 | 1, left, right, val);
}
// 修改完成后向上回溯修改父节点的值
pushUp(pos);
}
public int query(int pos, int left, int right) {
if (left <= tree[pos].left && tree[pos].right <= right) {
// 当前区间被包围
return tree[pos].val;
}
// 懒惰标记需要下传修改子节点的值
pushDown(pos);
int res = 0;
int mid = tree[pos].left + tree[pos].right >> 1;
if (left <= mid) {
res += query(pos << 1, left, right);
}
if (right > mid) {
res += query(pos << 1 | 1, left, right);
}
return res;
}
private void pushDown(int pos) {
// 根节点 和 懒惰标记为 0 的情况不需要再向下遍历
if (tree[pos].left != tree[pos].right && tree[pos].add != 0) {
int add = tree[pos].add;
// 计算累加变化量
tree[pos << 1].val += add * (tree[pos << 1].right - tree[pos << 1].left + 1);
tree[pos << 1 | 1].val += add * (tree[pos << 1 | 1].right - tree[pos << 1 | 1].left + 1);
// 子节点懒惰标记
tree[pos << 1].add += add;
tree[pos << 1 | 1].add += add;
// 懒惰标记清 0
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[pos << 1].val + tree[pos << 1 | 1].val;
}
}
相关题目
-
1893. 检查是否区域内所有整数都被覆盖
-
1109. 航班预订统计
3. 线段树动态开点
线段树的动态开点其实不难理解,它与我们上述直接创建好线段树所有节点不同,动态开点的线段树在 最初只创建一个根节点 代表整个区间,其他节点 只在需要的时候被创建,节省出了空间。当然,我们因此也不能再使用 pos << 1 和 pos << 1 | 1 来寻找当前节点的左右子节点,取而代之的是在节点中使用 left 和 right 记录左右子节点在 tree[] 中的位置,这一点需要注意:
static class Node {
// left 和 right 不再表示区间范围而是表示左右子节点在 tree 中的索引位置
int left, right;
int val;
int add;
}
我们以区间 [1, 5] 为例,创建区间 [5, 5] 为 14 的过程图示如下:
我们可以发现,会先创建默认的根节点 tree[1],之后创建出上图中 tree[2] 和 tree[3] 节点,而此时并没有找到区间 [5, 5],那么需要继续创建上图中的 tree[4] 和 tree[5] 节点(与直接创建出所有节点不同,如果是直接创建好所有节点的话它们的位置应该在 tree[6] 和 tree[7]),现在 tree[5] 节点表示的区间符合我们要找的条件,可以进行赋值和 pushUp 操作了,与直接创建出所有节点相比,动态开点少创建了 4 个节点,也就是图中标红的四个节点我们是没有创建的。
由于每次操作都可能创建并访问全新的一系列节点,因此 m 次单点操作后节点的空间复杂度是 O(mlogn),如果我们采用线段树动态开点解题的话,空间要开的尽可能大,Java 在 128M 可以开到 5e6 个节点以上。
结合图示大家应该能理解动态开点的过程了(不明白就自己画一遍),下面我们看下具体的代码:
/**
* 修改区间的值
*
* @param pos 当前节点的索引值
* @param left 当前线段树节点表示的范围下界
* @param right 当前线段树节点表示的范围上界
* @param l 要修改的区间下界
* @param r 要修改的区间上界
* @param val 区间值变化的大小
*/
public void update(int pos, int left, int right, int l, int r, int val) {
// 当前区间被要修改的区间全部包含
if (l <= left && right <= r) {
tree[pos].val += (right - left + 1) * val;
tree[pos].add += val;
return;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int mid = left + right >> 1;
if (l <= mid) {
update(tree[pos].left, left, mid, l, r, val);
}
if (r > mid) {
update(tree[pos].right, mid + 1, right, l, r, val);
}
pushUp(pos);
}
// 为该位置创建节点
private void lazyCreate(int pos) {
if (tree[pos] == null) {
tree[pos] = new Node();
}
// 创建左子树节点
if (tree[pos].left == 0) {
tree[pos].left = ++count;
tree[tree[pos].left] = new Node();
}
// 创建右子树节点
if (tree[pos].right == 0) {
tree[pos].right = ++count;
tree[tree[pos].right] = new Node();
}
}
private void pushDown(int pos, int len) {
if (tree[pos].left != 0 && tree[pos].right != 0 && tree[pos].add != 0) {
// 计算左右子树的值
tree[tree[pos].left].val += (len - len / 2) * tree[pos].add;
tree[tree[pos].right].val += len / 2 * tree[pos].add;
// 子节点懒惰标记
tree[tree[pos].left].add += tree[pos].add;
tree[tree[pos].right].add += tree[pos].add;
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[tree[pos].left].val + tree[tree[pos].right].val;
}
整体的逻辑并不难,新增的 lazyCreate 方法是动态开点的逻辑,需要注意的是执行区间更新时我们方法的参数中多了 left 和 right 表示当前节点区间范围的参数,因为我们现在的节点中只保存了左右子节点的位置,而没有区间信息,所以我们需要在参数中携带才行,否则我们没有办法判断当前区间和要找的区间是否匹配。
我还是将全量代码放在下面,方便大家学习:
public class SegmentTree3 {
static class Node {
// left 和 right 不再表示区间范围而是表示左右子节点在 tree 中的索引位置
int left, right;
int val;
int add;
}
// 记录当前节点数
int count;
Node[] tree;
public SegmentTree3() {
count = 1;
tree = new Node[(int) 5e6];
tree[count] = new Node();
}
public int query(int pos, int left, int right, int l, int r) {
if (l <= left && right <= r) {
return tree[pos].val;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int res = 0;
int mid = left + right >> 1;
if (l <= mid) {
res += query(tree[pos].left, left, mid, l, r);
}
if (r > mid) {
res += query(tree[pos].right, mid + 1, right, l, r);
}
return res;
}
/**
* 修改区间的值
*
* @param pos 当前节点的索引值
* @param left 当前线段树节点表示的范围下界
* @param right 当前线段树节点表示的范围上界
* @param l 要修改的区间下界
* @param r 要修改的区间上界
* @param val 区间值变化的大小
*/
public void update(int pos, int left, int right, int l, int r, int val) {
// 当前区间被要修改的区间全部包含
if (l <= left && right <= r) {
tree[pos].val += (right - left + 1) * val;
tree[pos].add += val;
return;
}
lazyCreate(pos);
pushDown(pos, right - left + 1);
int mid = left + right >> 1;
if (l <= mid) {
update(tree[pos].left, left, mid, l, r, val);
}
if (r > mid) {
update(tree[pos].right, mid + 1, right, l, r, val);
}
pushUp(pos);
}
// 为该位置创建节点
private void lazyCreate(int pos) {
if (tree[pos] == null) {
tree[pos] = new Node();
}
// 创建左子树节点
if (tree[pos].left == 0) {
tree[pos].left = ++count;
tree[tree[pos].left] = new Node();
}
// 创建右子树节点
if (tree[pos].right == 0) {
tree[pos].right = ++count;
tree[tree[pos].right] = new Node();
}
}
private void pushDown(int pos, int len) {
if (tree[pos].left != 0 && tree[pos].right != 0 && tree[pos].add != 0) {
// 计算左右子树的值
tree[tree[pos].left].val += (len - len / 2) * tree[pos].add;
tree[tree[pos].right].val += len / 2 * tree[pos].add;
// 子节点懒惰标记
tree[tree[pos].left].add += tree[pos].add;
tree[tree[pos].right].add += tree[pos].add;
tree[pos].add = 0;
}
}
private void pushUp(int pos) {
tree[pos].val = tree[tree[pos].left].val + tree[tree[pos].right].val;
}
}
相关题目
-
729. 我的日程安排表 I 中等
-
731. 我的日程安排表 II 中等
-
732. 我的日程安排表 III 困难
-
715. Range 模块 困难
巨人的肩膀
-
【宫水三叶】一题三解 :「递归分治」&「线段树」&「单调栈」
-
线段树浅谈
-
线段树什么的不是简简单单嘛,我教你!:基础篇
-
OI-wiki 线段树
-
维基百科:线段树
-
【RMQ 专题】关于 RMQ 的若干解法(内含彩蛋)
-
【宫水三叶】一题双解 :「差分」&「线段树」(附区间求和目录)
-
【宫水三叶】一题三解 :「模拟」&「线段树(动态开点)」&「分块 + 位运算(分桶)」