Day 2 数组: 977. 有序数组的平方, 209. 长度最小的子数组, 59. 螺旋矩阵 II
977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
进阶:
请你设计时间复杂度为 O(n) 的算法解决本问题
暴力解法:
先把每一个元素都变成平方,再进行sort()。
class Solution(object):
def sortedSquares(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
对于平方这个步骤,time: O(n),space: O(1);
对于排序这个步骤,Python的sort函数使用了TimSort算法,其平均和最坏的时间复杂度都是
O(nlog n)。对于空间复杂度,由于TimSort是一种稳定的排序算法,它需要O(n)的额外空间
来存储临时数据。因此
time: O(nlogn)
space: O(n)
"""
# 暴力解法:
for i in range(0, len(nums)):
nums[i] = nums[i] * nums[i]
nums.sort()
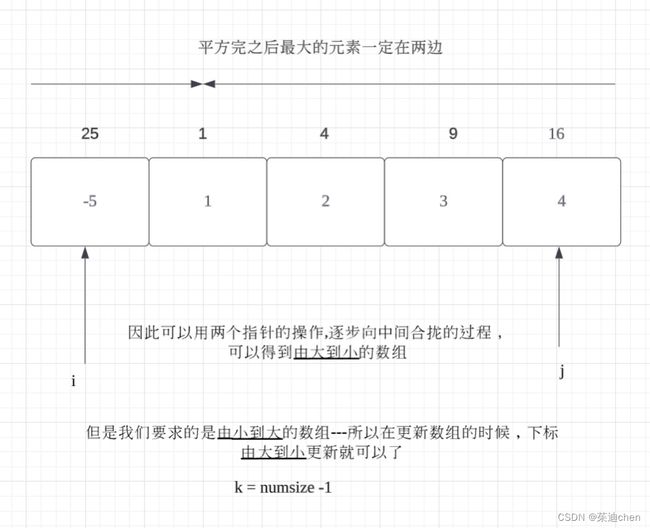
return nums双指针解法:
我们需要得到的是由小到大的数组,所以在更新数组的时候应该由大到小更新数组。
定义一个左指针i, 一个右指针j, 当i <= j 的时候,循环要一直进行下去。
如果nums[i] * nums[i]最大,即nums[i] * nums[i] > nums[j] * nums[j], 则 i ++, k --;
如果nums[j] * nums[j]最大,即nums[i] * nums[i] < nums[j] * nums[j], 则 j --, k --。
对于第二点,可以用else来进行操作,来包括即nums[i] * nums[i] <= nums[j] * nums[j] 的操作。因为相等的时候,更新 i 还是 j 都是一样的。
class Solution(object):
def sortedSquares(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
time: O(n),因为我们只需要对数组进行一次遍历
space: O(1),因为我们只使用了固定的额外空间。
"""
# 双指针解法
k = len(nums) - 1 # 用于更新nums数组(list)
i = 0 # 左指针
j = len(nums) - 1 # 右指针
res = [0] * len(nums) # 需要提前定义列表,存放结果
while i <= j:
if (nums[i] * nums[i] > nums[j] * nums[j]):
res[k] = nums[i] * nums[i]
i += 1
k -= 1
else:
res[k] = nums[j] * nums[j]
j -= 1
k -= 1
return res209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:输入:target = 4, nums = [1,4,4]
输出:1
示例 3:输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
本题关键在于理解滑动窗口。
滑动窗口和之前的双指针思路相似,也是用两个指针。只不过两个指针中间的元素更像是一个正在滑动的窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
滑动窗口也是用一层for循环,做两层for循环的事。
for(j )的for循环里的j,指向的一定是终止位置。
滑动窗口最重要的一点是,如何移动起始位置?动态移动的策略。
用if还是while?if只更新一次,但是我们是需要持续更新起始位置下标的,因此用while。
注意题目中:如果不存在符合条件的子数组,返回 0
因此要写一下basic case下等于0。
class Solution(object):
def minSubArrayLen(self, target, nums):
"""
:type target: int
:type nums: List[int]
:rtype: int
time: O(n)
space: O(1)
"""
if not nums or nums is None:
return 0
res = float('inf') #初始化返回的长度,使其等于最大值
cur_sum = 0 # 当前累加值
left = 0 # 起始位置
# right = 0 # 终止位置
for right in range(0, len(nums)):
cur_sum += nums[right]
while cur_sum >= target:
res = min(res,right - left + 1)
cur_sum = cur_sum - nums[left]
left += 1
return res if res != float('inf') else 0
这段代码我本来错了一个小的地方,因为我没看清题目“其和 ≥ target 的长度最小的”,所以只写了cur_sum > target:,最后才发现错误然后更新为cur_sum >= target:。
59. 螺旋矩阵 II
"螺旋矩阵 II"的题目要求根据一个给定的整数n,生成一个包含1到n²所有元素的方阵,元素按螺旋顺序从左上角开始填充。
这个解法的主要思路是定义一个n×n的二维矩阵,并定义上下左右四个边界,然后依次按照从左到右、从上到下、从右到左、从下到上的顺序进行填充,每填充一个元素,数值就加1,直到填充所有的元素。每一轮填充完成后,相应的边界就向内缩小,以此类推,直到所有的元素都被填充。
class Solution(object):
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
# 初始化二维矩阵
matrix = [[0]*n for _ in range(n)]
# 定义上下左右边界
up = 0
down = n - 1
left = 0
right = n - 1
num = 1 # 初始值
while num <= n * n:
# 从左到右填充上边界
for i in range(left, right + 1):
matrix[up][i] = num
num += 1
up += 1
# 从上到下填充右边界
for i in range(up, down + 1):
matrix[i][right] = num
num += 1
right -= 1
# 从右到左填充下边界
for i in range(right, left - 1, -1):
matrix[down][i] = num
num += 1
down -= 1
# 从下到上填充左边界
for i in range(down, up - 1, -1):
matrix[i][left] = num
num += 1
left += 1
return matrix