深度学习-4-二维目标检测-YOLOv5理论模型详解
YOLOv5理论模型详解
1.Yolov5四种网络模型
Yolov5官方代码中,给出的目标检测网络中一共有4个版本,分别是Yolov5s、Yolov5m、Yolov5l、Yolov5x四个模型。
YOLOv5系列的四个模型(YOLOv5s、YOLOv5m、YOLOv5l、YOLOv5x)在参数量和性能上有所不同。参数量指的是模型中需要学习的参数的数量,通常表示模型的复杂度和容量。四个模型的网络结构是相同的,它们都是基于YOLOv5的骨干网络,但是随着模型的增大(从s到x),参数量也会增加,从而提供更高的性能和更准确的检测结果。
学习一个新的算法,最好在脑海中对算法网络的整体架构有一个清晰的理解。但Yolov5代码中给出的网络文件是yaml格式和原本Yolov3、Yolov4中的cfg不同,无法用netron工具直接可视化的查看网络结构。
因此可以采用pt->onnx->netron的折中方式,先使用Yolov5代码中models/export.py脚本将pt文件转换为onnx格式,再用netron工具打开,查看全网络的整体架构。
1.1Yolov5网络结构图
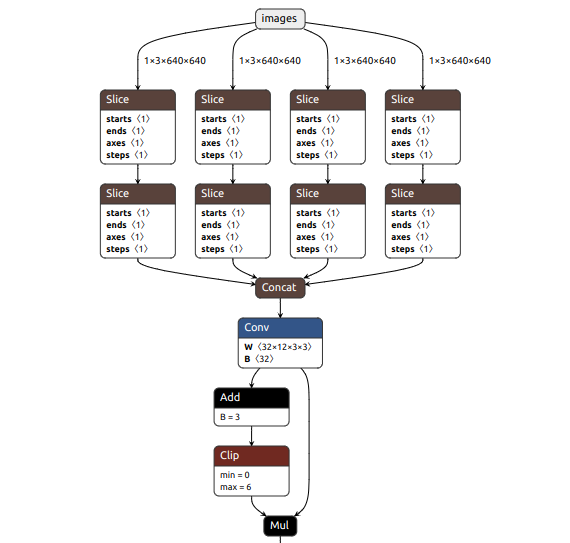
利用netron工具可以可视化的打开Yolov5的网络结构
1.2网络结构可视化
将四种模型的pt文件转换成对应的onnx文件后,使用netron工具查看。
先安装ONNX模块,转换pt文件
# for ONNX export
pip install onnx>=1.7.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
# for CoreML export
pip install coremltools==4.0 -i https://pypi.tuna.tsinghua.edu.cn/simple# export at 640x640 with batch size 1
python models/export.py --weights weights/yolov5s.pt --img 640 --batch 1
然后浏览器在线使用NETRON工具,打开yolov5s.onnx模型文件
Yolov5s网络是Yolov5四种模型中深度最小,特征图的宽度最小的网络。后面3种都是在此基础上不断加深,不断加宽。
2.Yolov5网络模型详解
2.1概述
YOLOv5在YOLOv4算法的基础上做了进一步的改进,检测性能得到进一步的提升。虽然YOLOv5算法并没有与YOLOv4算法进行性能比较与分析,但是YOLOv5在COCO数据集上面测试的效果还是挺不错的。虽然YOLOv5的这些改进思路看来比较简单或者创新点不足,但是它们确实可以提升检测算法的性能。其实工业界往往更喜欢使用这些方法,而不是利用一个超级复杂的算法来获得较高的检测精度。
下面将对YOLOv5检测算法中提出的改进思路进行详细的解说,可以尝试将这些改进思路应用到其它的目标检测算法中。
主要的改进思路如下所示:
- 输入端:在模型训练阶段,提出了一些改进思路,主要包括Mosaic数据增强、自适应锚框计算、自适应图片缩放;
- 基准网络:融合其它检测算法中的一些新思路,主要包括:Focus结构与CSP结构;
- Neck网络:目标检测网络在BackBone与最后的Head输出层之间往往会插入一些层,Yolov5中添加了FPN+PAN结构;
- Head输出层:输出层的锚框机制与YOLOv4相同,主要改进的是训练时的损失函数GIOU_Loss,以及预测框筛选的DIOU_nms。
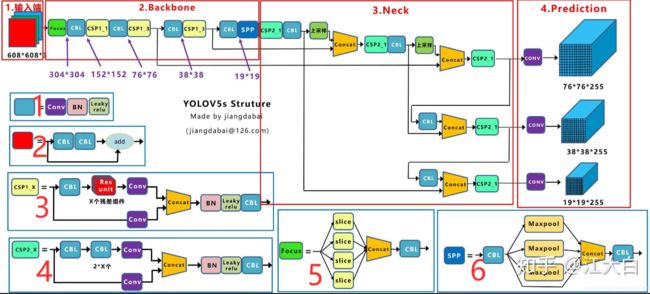
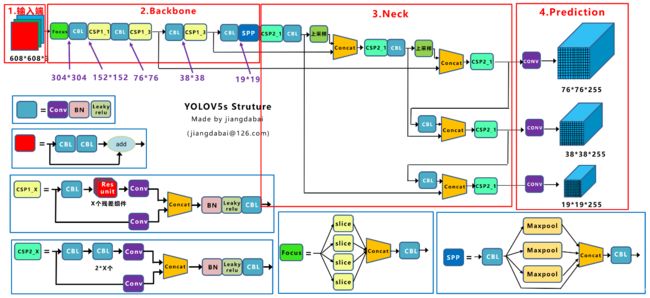
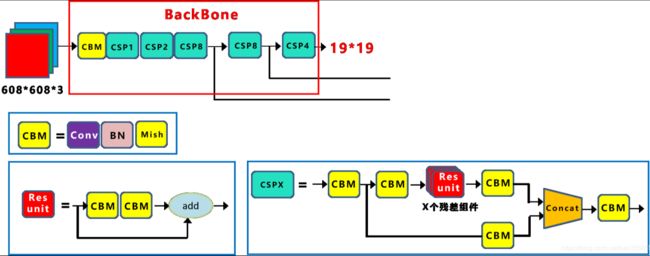
Yolov5采用的基础组件
- CBL-CBL模块由Conv+BN+Leaky_relu激活函数组成,如上图中的模块1所示。
- Res unit-借鉴ResNet网络中的残差结构,用来构建深层网络,CBM是残差模块中的子模块,如上图中的模块2所示。
- CSP1_X-借鉴CSPNet网络结构,该模块由CBL模块、Res unint模块以及卷积层、Concat组成而成,如上图中的模块3所示。
- CSP2_X-借鉴CSPNet网络结构,该模块由卷积层和X个Res unint模块Concat组成而成,如上图中的模块4所示。
- Focus-如上图中的模块5所示,Focus结构首先将多个slice结果Concat起来,然后将其送入CBL模块中。
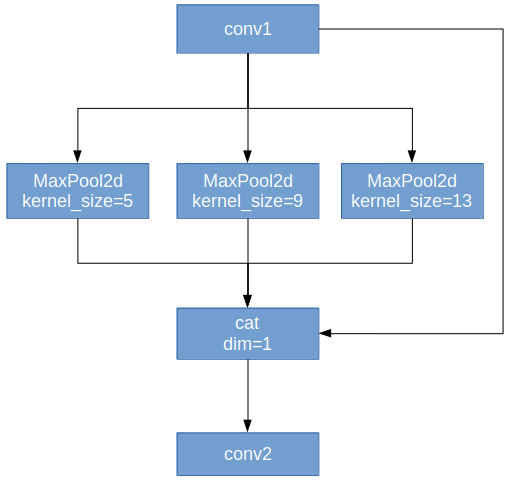
- SPP-采用1×1、5×5、9×9和13×13的最大池化方式,进行多尺度特征融合,如上图中的模块6所示。
2.2网络结构演进
Yolov3网络结构是比较经典的one-stage结构,分为输入端、Backbone、Neck和Prediction四个部分。
Yolov4的网络结构在Yolov3的基础上进行了很多创新,比如:
- 输入端采用mosaic数据增强
- Backbone上采用了CSP、Darknet53、Mish激活函数、Dropblock等方式
- Neck中采用了SPP、FPN+PAN的结构
- 输出端则采用CIOU_Loss、DIOU_nms操作
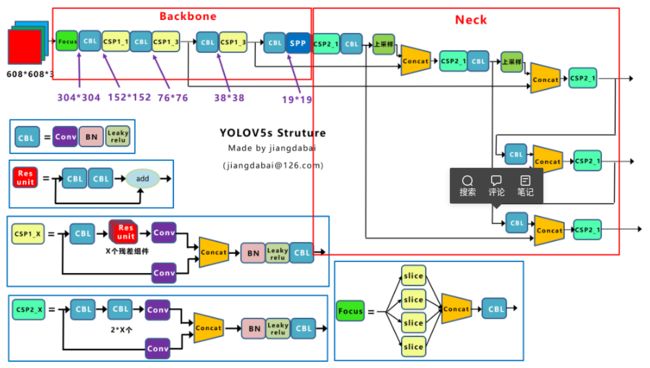
Yolov5的网络结构,整体上还是分为输入端、Backbone、Neck、Prediction四个部分。
与Yolov3比较,主要的不同点如下:
- 输入端:Mosaic数据增强、自适应锚框计算
- Backbone:Focus结构、CSP结构
- Neck:FPN+PAN结构
- Prediction:GIOU_Loss
Yolov5作者在COCO数据集上进行了算法性能测试,Yolov5s网络模型最小,速度最块,AP精度也最低。其他的三种规模的网络模型,是在它的基础上加深和加宽网络得到的,AP精度在不断提升,但GPU速度的消耗也在不断增加。
2.3Yolov5输入端
输入端表示输入的图片。该网络的输入图像大小为608*608,该阶段通常包含一个图像预处理阶段,即将输入图像缩放到网络的输入大小,并进行归一化等操作。在网络训练阶段,YOLOv5使用Mosaic数据增强操作提升模型的训练速度和网络的精度;并提出了一种自适应锚框计算与自适应图片缩放方法。
(1)Mosaic数据增强
Mosaic数据增强是采用4张图片,通过随机缩放、随机裁剪、随机排布的方式进行拼接,在丰富数据集的同时极大的提升网络的训练速度,而且可以降低模型的内存需求,这对于小目标的训练检测效果还是很不错的。
为什么要进行Mosaic数据增强?
在平时项目训练时,小目标的AP一般比中目标和大目标低很多。而Coco数据集中也包含大量的小目标,但比较麻烦的是小目标的分布并不均匀。
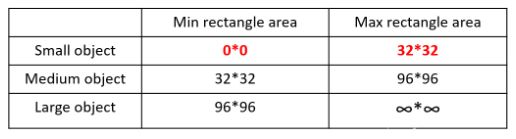
大、中、小目标的定义,小目标是目标框的长宽0*0-32*32之间的物体。
如上表所示COCO数据集的统计,三种尺度的目标占比并不均衡。在所有的训练集图片中,只有52.3% 的图片有小目标,而中目标和大目标的分布相对来说更加均匀一些。
因此采用Mosaic数据增强的主要优点;
a.丰富数据集:随机选用四张图片,随机缩放,在随机分布进行拼接,大大丰富了检测数据集,特别是随机缩放增加了很多小目标,让网络的鲁棒性更好。
b.减少GPU:这样可以直接计算4张图片的数据,使得Min-batch大小并不需要很大,一个GPU就可以达到比较好的效果。
(2)自适应锚框计算
在Yolo系列算法中,针对不同的数据集,都会有初始设定长宽的锚框。在网络训练中,网络在初始锚框的基础上输出预测框,进而与真实框groundtruth进行对比,计算两者差距,再反向更新,迭代网络参数。因此初始锚框也是比较重要的一部分,比如Yolov5在Coco数据集上初始设定的锚框:
在Yolov3、Yolov4中,训练不同的数据集时,计算初始锚框的值是通过单独的程序运行的。
但Yolov5中将此功能嵌入到代码中,每次训练时,自适应的计算不同训练集中的最佳锚框值。当然,如果觉得计算的锚框效果不是很好,也可以在代码中将自动计算锚框功能关闭。控制的代码即train.py中的一行代码,设置成False,每次训练时,不会自动计算。
![]()
(3)自适应图片缩放
在常用的目标检测算法中,不同的图片长宽都不相同,因此常用的方式是将原始图片统一缩放到一个标准尺寸,再送入检测网络中。比如Yolo算法中常用416×416,608×608等尺寸,比如对下面800*600的图像进行变换。
Yolov5代码中对此进行了改进,也是Yolov5推理速度能够很快的一个不错的trick(技巧)。
因为在项目实际使用时,很多图片的长宽比不同,所以缩放填充后,两端的黑边宽度不同。如果填充的比较多,则存在信息冗余,影响推理速度。
Yolov5代码中datasets.py的letterbox函数进行了修改,对原始图像自适应的添加最少的黑边。图像高度上两端的黑边变少了,在推理时,计算量也会减少,及目标检测速度会得到提升。
Yolov5中datasets.py的letterbox函数采用的具体计算方法是:
第一步:计算缩放比例
原始缩放尺寸是416×416,都除以原始图像的尺寸后,可以得到0.52,和0.69两个缩放系数,选择小的缩放系数0.52。
第二步:计算缩放后的尺寸
原始图片的长宽都乘以最小的缩放系数0.52,宽变成了416,而高变成了312。
第三步:计算黑边填充数值
将416-312=104,得到原本需要填充的高度。再采用numpy中np.mod取余数的方式,得到8个像素,再除以2,即得到图片高度两端需要填充的数值。
a.这里填充的是黑色,即(0,0,0),而Yolov5中填充的是灰色,即(114,114,114),都是一样的效果。
b.训练时没有采用缩减黑边的方式,还是采用传统填充的方式,即缩放到416×416大小。只是在测试,使用模型推理时,才采用缩减黑边的方式,提高目标检测,推理的速度。
c.为什么np.mod函数的后面用32?因为Yolov5的网络经过5次下采样,而2的5次方,等于32。所以至少要去掉32的倍数,再进行取余。
2.4 Backbone
骨干网络通常是一些性能优异的分类器中的网络,该模块用来提取一些通用的特征表示。YOLOv5中不仅使用了CSPDarknet53结构,而且使用了Focus结构作为骨干网络。
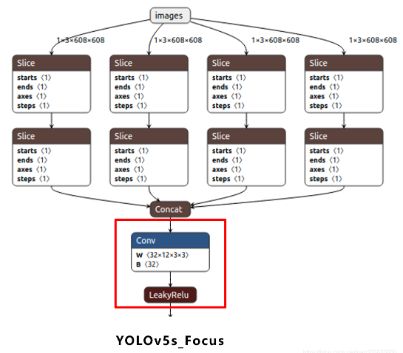
(1) Focus结构
Focus结构,在Yolov3&Yolov4中并没有这个结构,其中比较关键的是切片操作。右图的切片示意图,4*4*3的图像切片后变成2*2*12的特征图。作用是减少浮点计算量,增加计算速度。
以Yolov5s的结构为例,原始608*608*3的图像输入Focus结构,采用切片操作,先变成304*304*12的特征图,再经过一次32个卷积核的卷积操作,最终变成304*304*32的特征图。
Yolov5s的Focus结构最后使用了32个卷积核,而其他三种结构,使用的数量有所增加。
(2) CSP结构
Cross Stage Partial Network (跨阶段局部网络)
YOLOv4网络结构中,借鉴了CSPNet的设计思路,在主干网络中设计了CSP结构。
Yolov5与Yolov4不同点在于,Yolov4中只有主干网络使用了CSP结构,而Yolov5中设计了两种CSP结构,以Yolov5s网络为例,以CSP1_X结构应用于Backbone骨干网络,另一种CSP2_X结构则应用在Neck中。
YOLOv5s的CSP结构是将原输入分成两个分支,分别进行卷积操作使得通道数减半,然后一个分支进行Bottleneck * N操作,然后concat两个分支,使得BottlenneckCSP的输入与输出是一样的大小,这样是为了让模型学习到更多的特征。
CSP1_X结构
BottleneckCSP的网络结构图如下图所示:
其中CBS为Conv+BN+SiLu,后期的图中CBL(conv+BN+Leaky relu)需要改成CBS(conv+BN+SiLU)。其中Resunit是x个残差组件。
将输入分为两个分支,一个分支先通过CBS,再经过多个残差结构(Bottleneck * N),再进行一次卷积;另一个分支直接进行卷积;然后两个分支进行concat,再经过BN(正态分布),再来一次激活(之前的版本是Leaky,后面是SiLU),最后进行一个CBS。
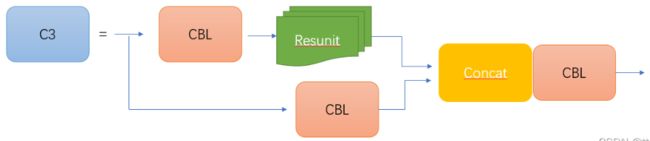
C3的网络结构图如下图所示:
CSP1_X应用于backbone主干网络部分,backbone是较深的网络,增加残差结构可以增加层与层之间反向传播的梯度值,避免因为加深而带来的梯度消失,从而可以提取到更细粒度的特征并且不用担心网络退化。
CSP2_X结构
BottleneckCSP的网络结构图如图所示
C3的网络结构图如图所示
CSP2_X相对于CSP1_X来说,不一样的地方只有CSP2_X将Resunit换成了2 * X个CBS,主要应用在Neck网络 (网络没那么深)。同样的,之前的版本是Leaky,后期是SiLU)
(3) SPP组件
空间金字塔池化,能将任意大小的特征图转换成固定大小的特征向量。
在卷积神经网络中,不固定输入尺寸的方法有下面三种:
- 对输入进行resize操作,让他们统统变成你设计的层的输入规格那样。但是这样过于暴力直接,可能会丢失很多信息或者多出很多不该有的信息(图片变形等),影响最终的结果。
- 替换网络中的全连接层,对最后的卷积层使用global average pooling,全局平均池化只和通道数有关,而与特征图大小没有关系
- 最后一个就是SPP结构
在yolov5中SPP作用是:实现局部特征和全局特征的featherMap级别的融合。
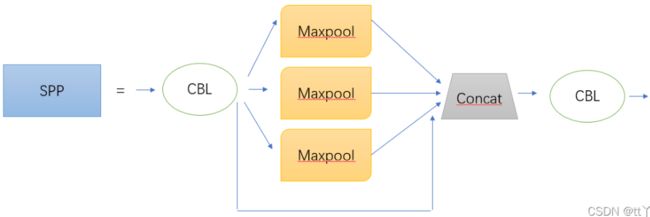
在YOLOv5中SPP的结构图如下图所示:
分别对1 * 1分块,5*5分块,9*9分块和13 *13分块的子图里分别取每一个框内的max值,这一步就是作最大池化,这样最后提取出来的特征值一共有1 * 1 + 5 * 5 + 9 * 9 = 107个。得出的特征再concat在一起。
2.5 Neck
Neck网络通常位于基准网络和头部网络的中间位置,利用它可以进一步提升特征的多样性及鲁棒性。虽然YOLOv5同样用到了SPP模块、FPN+PAN模块,但是实现的细节有些不同。
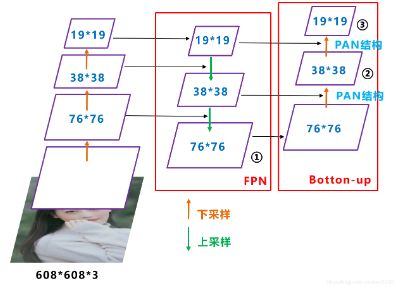
Yolov5的Neck和Yolov4中一样,都采用FPN+PAN的结构,但在Yolov5刚出来时,只使用了FPN结构,后面才增加了PAN结构,此外网络中其他部分也进行了调整。
2.6 Head输出端
Head用来完成目标检测结果的输出。针对不同的检测算法,输出端的分支个数不尽相同,通常包含一个分类分支和一个回归分支。YOLOv4利用GIOU_Loss来代替Smooth L1 Loss函数,从而进一步提升算法的检测精度。
(1)Bounding box损失函数
目标检测任务的损失函数一般由Classificition Loss(分类损失函数)和Bounding Box Regeression Loss(回归损失函数)两部分构成。
Bounding Box Regeression的Loss近些年的发展过程是:Smooth L1 Loss-> IoU Loss(2016)-> GIoU Loss(2019)-> DIoU Loss(2020)->CIoU Loss(2020)
a. IOU_Loss
根据IOU计算的loss很简单,主要是交集/并集,但也存在两个问题。
问题1:即状态1的情况,当预测框和目标框不相交时,IOU=0,无法反应两个框距离的远近,此时损失函数不可导,IOU_Loss无法优化两个框不相交的情况。
问题2:即状态2和状态3的情况,当两个预测框大小相同,两个IOU也相同,IOU_Loss无法区分两者相交情况的不同。
因此2019年出现了GIOU_Loss来进行改进。
b. GIOU_loss
上图GIOU_Loss中,增加了相交尺度的衡量方式,缓解了单纯IOU_Loss时的尴尬。
但还存在一种不足:
问题:状态1、2、3都是预测框在目标框内部且预测框大小一致的情况,这时预测框和目标框的差集都是相同的,因此这三种状态的GIOU值也都是相同的,这时GIOU退化成了IOU,无法区分相对位置关系。基于这个问题,2020年的AAAI又提出了DIOU_Loss。
c. DIOU _loss
好的目标框回归函数应该考虑三个重要几何因素:重叠面积、中心点距离,长宽比。
针对IOU和GIOU存在的问题,作者从两个方面进行考虑
一:如何最小化预测框和目标框之间的归一化距离?
二:如何在预测框和目标框重叠时,回归的更准确?
针对第一个问题,提出了DIOU_Loss(Distance_IOU_Loss)
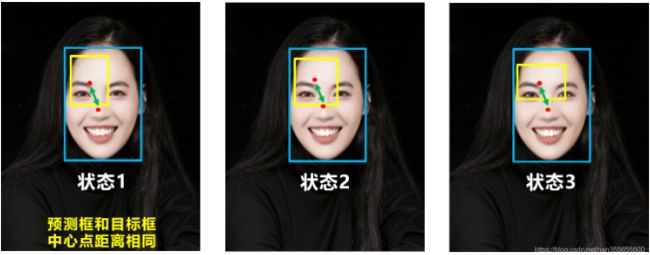
DIOU_Loss考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量2个框的距离,因此DIOU_Loss收敛的更快。但就像前面好的目标框回归函数所说的,这时并没有考虑到长宽比。
问题:比如上面三种状态,目标框包裹预测框,但预测框的中心点的位置都是一样的,因此按照DIOU_Loss的计算公式,三者的值都是相同的。
d. CIOU_loss
CIOU_Loss是在DIOU_Loss基础上还增加了一个影响因子,将预测框和目标框的长宽比都考虑了进去。
综合来看各个Loss函数的不同点:
IOU_Loss:主要考虑检测框和目标框重叠面积。
GIOU_Loss:在IOU的基础上,解决边界框不重合时的问题。
DIOU_Loss:在IOU和GIOU的基础上,考虑边界框中心点距离的信息。
CIOU_Loss:在DIOU的基础上,考虑边界框宽高比的尺度信息。
Yolov5中采用其中的CIOU_Loss做Bounding box的损失函数,使预测框回归的速度和精度更高一些。
(2)NMS非极大值抑制
在目标检测的后处理过程中,针对很多目标框的筛选,通常需要NMS操作。
Yolov4在DIOU_loss的基础上采用DIOU_nms的方式,而Yolov5中仍然采用加权nms的方式。可以看出,采用DIOU_nms,下方中间箭头的黄色部分,原本被遮挡的摩托车也可以检出。
采用了DIOU_nms的方式,在同样的参数情况下,将nms中IOU修改成DIOU_nms。对于一些遮挡重叠的目标,确实会有一些改进。在参数和普通的IOU_nms一致的情况下,修改成DIOU_nms,可以将两个目标检出。虽然大多数状态下效果差不多,但在不增加计算成本的情况下,有稍微的改进也是好的。
3. Yolov5四种网络结构的不同点
Yolov5的四种网络结构,都是以yaml文件的形式来呈现的。四个文件的内容基本上都是一样的,只有最上方的depth_mutiple和width_mutiple两个参数不同。
如何通过两个参数控制四种网络结构?
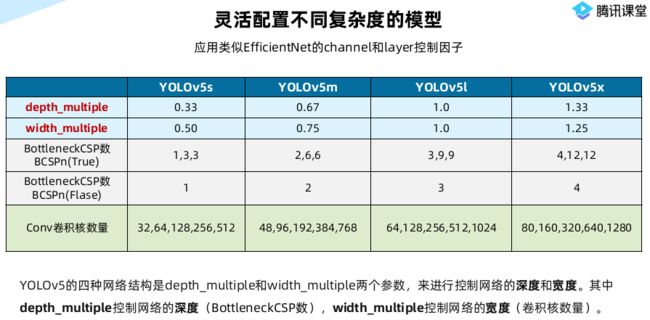
3.1四种网络结构的参数
Yolov5的四种网络结构有区别的两个参数:
通过上面的两个参数,来进行控制网络的深度和宽度。其中depth_multiple控制网络的深度,width_multiple控制网络的宽度。
3.2 Yolov5网络结构
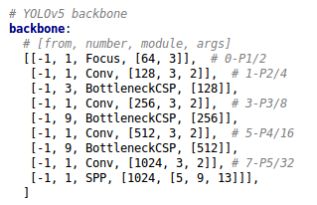
四种结构的yaml文件中,下方的网络架构代码都是一样的。将其中的Backbone部分提取出来,讲解如何控制网络的宽度和深度,Head部分也是同样的原理。
在对网络结构进行解析时,yolo.py中下方的这一行代码将四种结构的depth_multiple,width_multiple提取出,赋值给gd,gw。后面主要对这gd,gw这两个参数进行讲解。
![]()
3.3 Yolov5四种网络的深度
(1)不同网络的深度
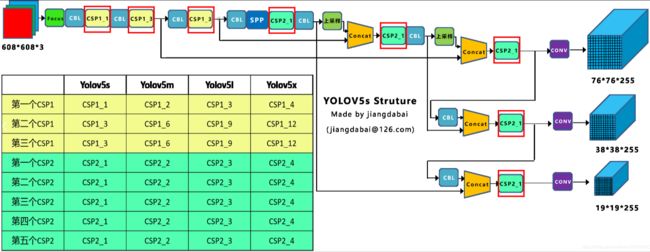
上图中是Yolov5的两种CSP结构,CSP1结构主要应用于Backbone中,CSP2结构主要应用于Neck中。四种网络结构的CSP结构的深度都是不同的。
a. Yolov5s的CSP1结构中使用了1个残差组件,因此是CSP1_1。Yolov5m增加了网络的深度,增加了CSP结构中使用的残差组件。
b. CSP2结构中的残差组件个数,在四种网络结构中不断加深,在不断增加网络特征提取和特征融合的能力。
(2)控制深度的代码
控制四种网络结构的核心代码是yolo.py中下面的代码,存在两个变量,n和gd。
将n和gd带入计算,看每种网络的变化结果。
![]()
(3)验证控制深度的有效性
选择最小的yolov5s.yaml和中间的yolov5l.yaml两个网络结构,将gd(height_multiple)系数带入,看是否正确。
a. yolov5s.yaml
其中depth_multiple=0.33,即gd=0.33,而n则由上面红色框中的信息获得。
以上面网络框图中的第一个CSP1为例,即上面的第一个红色框。n等于第二个数值3。
而gd=0.33,带入(2)中的计算代码,结果n=1。因此第一个CSP1结构内只有1个残差组件,即CSP1_1。
第二个CSP1结构中,n等于第二个数值9,而gd=0.33,带入(2)中计算,结果n=3,因此第二个CSP1结构中有3个残差组件,即CSP1_3。
第三个CSP1结构也是同理。
b. yolov5l.xml
其中depth_multiple=1,即gd=1
和上面的计算方式相同,第一个CSP1结构中,n=3,带入代码中,结果n=3,因此为CSP1_3。
下面第二个CSP1结构和第三个CSP1结构都是同样的原理。
3.4 Yolov5四种网络的宽度
(1)不同网络的宽度
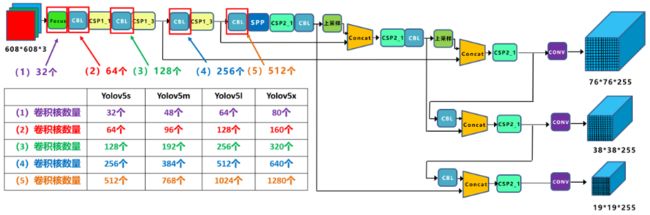
如上图所示,四种Yolov5结构在不同阶段的卷积核的数量都是不一样的。因此也直接影响卷积后特征图的第三维度,即厚度,这里表示为网络的宽度。
a. 以Yolov5s结构为例,第一个Focus结构中,最后卷积操作时,卷积核的数量是32个,因此经过Focus结构,特征图的大小变成34*304*32。Yolov5m的Focus结构中的卷积操作使用了48个卷积核,因此Focus结构后的特征图变成304×304×48。Yolov5l,Yolov5x也是同样的原理。
b. 第二个卷积操作时,Yolov5s使用了64个卷积核,因此得到的特征图是152×152×64。而Yolov5m使用96个特征图,因此得到的特征图是152×152×96。Yolov5l,Yolov5x也是同理。
四种不同结构的卷积核的数量不同,这也直接影响网络中比如CSP1结构,CSP2等结构,以及各个普通卷积,卷积操作时的卷积核数量也同步在调整,影响整体网络的计算量。
当然卷积核的数量越多,特征图的厚度,即宽度越宽,网络提取特征的学习能力也越强。
(2)控制宽度的代码
在Yolov5的代码中,控制宽度的核心代码是yolo.py文件里面的这一行:
![]()
这里调用的函数make_divisible的功能是:
(3)验证控制宽度的有效性
选择Yolov5s和Yolov5l两个网络结构,将width_multiple系数带入,看是否正确。
a. yolov5s.yaml
其中width_multiple=0.5,即gw=0.5
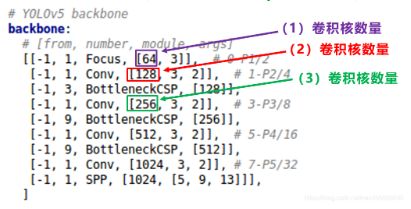
以第一个卷积下采样为例,即Focus结构中下面的卷积操作。按照上面Backbone的信息,在Focus中,标准的c2=64,而gw=0.5,代入(2)中的计算公式,最后的结果=32。即Yolov5s的Focus结构中,卷积下采样操作的卷积核数量为32个。
计算后面的第二个卷积下采样操作,标准c2的值=128,gw=0.5,代入(2)中公式,最后的结果=64,也是正确的。
b. yolov5l.yaml
其中width_multiple=1,即gw=1,而标准的c2=64,代入上面(2)的计算公式中,可以得到Yolov5l的Focus结构中,卷积下采样操作的卷积核的数量为64个,而第二个卷积下采样的卷积核数量是128个。
另外的三个卷积下采样操作,以及Yolov5m,Yolov5x结构也是同样的计算方式。
4. 在小目标分割检测上的研究
目标检测发展很快,但对于小目标的检测还是有一定的瓶颈,特别是大分辨率图像的小目标检测。比如7920*2160,甚至是16000*16000像素的图像。
图像的分辨率很大,但又有很多小的目标需要检测。如果直接输入检测网络,比如Yolov3,检出效果并不好。
4.1Yolo检测效果不好的主要原因
(1)小目标尺寸
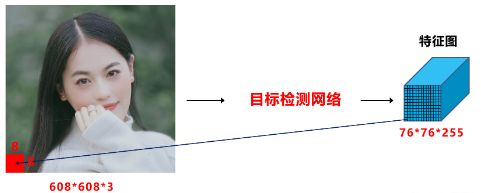
以网络的输入608×608为例,Yolov3、Yolov4,Yolov5中下采样都使用了5次,因此最后的特征图大小是19×19,38×38,76×76。
三个特征图中,最大的76×76负责检测小目标,而对应到608×608上,每格特征图的感受野是608/76=8×8大小。
将608×608对应到7680×2160上,以最长边7680为例,7680/608×8=101。即如果原始图像中目标的宽或高小于101像素,网络很难学习到目标的特征信息。(这里忽略多尺度训练的因素及增加网络检测分支的情况)
(2)高分辨率
在很多遥感图像中,长宽比的分辨率比7680*2160更大。如果直接输入原图检测,很多小目标都无法检测出。
(3)显卡爆炸
很多图像分辨率很大,如果简单的进行下采样,下采样的倍数太大,容易丢失数据信息。但是倍数太小,网络前向传播需要在内存中保存大量的特征图,极大耗尽GPU资源,很容易发生显卡爆炸显存爆炸,无法正常的训练及推理。
可以借鉴2018年YOLT算法的方式,改变一下思维,对大分辨率图片先进行分割,变成一张张小图,再进行检测。
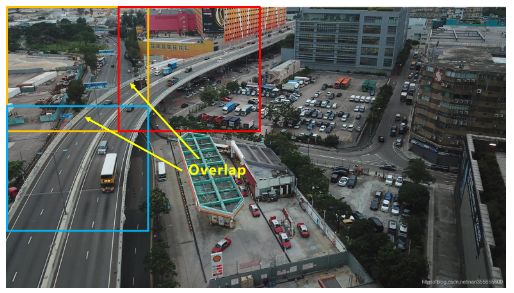
需要注意的是:
为了避免两张小图之间,一些目标正好被分割截断,所以两个小图之间需要设置overlap重叠区域,比如分割的小图是960×960像素大小,则overlap可以设置为960×20%=192像素。
每个小图检测完成后,再将所有的框放到大图上,对大图整体做一次nms操作,将重叠区域的很多重复框去除。这样操作,可以将很多小目标检出,比如16000×16000像素的遥感图像。
说明:这里关于小图检测后,放到大图上的方法,采用的方式,其实按照在大图上裁剪的位置,直接回归到大图即可。
国内还有一个10亿像素图像目标检测的比赛,也是用的这样的方式,有相应的讲解视频。
无人机视角下,也有很多小的目标。这里也进行了测试,效果还是不错的。比如下图是将原始大图->416×416大小,直接使用目标检测网络输出的效果:
可以看到中间黄色框区域,很多汽车检测漏掉。再使用分割的方式,将大图先分割成小图,再对每个小图检测,可以看出中间区域很多的汽车都被检测出来:
这样处理的方式既有优点也有缺点:
优点:
(1)准确性
分割后的小图,再输入目标检测网络中,对于最小目标像素的下限会大大降低。比如分割成608×608大小,送入输入图像大小608×608的网络中,按照上面的计算方式,原始图片上,长宽大于8个像素的小目标都可以学习到特征。
(2)检测方式
在大分辨率图像,比如遥感图像,或者无人机图像,如果无需考虑实时性的检测,且对小目标检测也有需求的项目,可以尝试此种方式。
缺点:
(1) 增加计算量
比如原本7680×2160的图像,如果使用直接大图检测的方式,一次即可检测完。但采用分割的方式,切分成N张608×608大小的图像,再进行N次检测,会大大增加检测时间。
借鉴Yolov5的四种网络方式,我们可以采用尽量轻的网络,比如Yolov5s网络结构或者更轻的网络。当然Yolov4和Yolov5的网络各有优势,我们也可以借鉴Yolov5的设计方式,对Yolov4进行轻量化改造,或者进行剪枝。
在实际测试中,Yolov4的准确性有不错的优势,但Yolov5的多种网络结构使用起来更加灵活,我们可以根据不同的项目需求,取长补短,发挥不同检测网络的优势。