递归算法（二）-分治法

分治法

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

分治法解题的一般步骤：

1. 分解，将要解决的问题划分成若干规模较小的同类问题；
2. 求解，当子问题划分得足够小时，用较简单的方法解决；
3. 合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

实现方法：分治法一般是通过递归调用实现的。例如排序算法(快速排序，归并排序)，傅里叶变换(快速傅里叶变换)等。

分治法使用场景

1. 该问题的规模缩小到一定的程度就可以容易的解决。
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解。
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

第一条特征是绝大多数问题可以满足的，问题的复杂性一般是随着问题规模的增加而增加；第二条特征是应用分治法的前提。它是大多数问题可以满足的，此特征反映了递归思想的应用。第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条，而不具备第三条特征，则可以考虑使用贪心法或者动态规划法。第四条关系到分治法的效率，如果各个子问题是不独立的则分治法要做寻多不必要的工作，重复的解决公共的子问题，此时虽然可用分治法，但一般使用动态规划法较好。

归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

def merge_sort(alist):
    # 终止条件
    if len(alist) <= 1:
        return alist
    # 二分分解
    num = len(alist)//2
    left = merge_sort(alist[:num])
    right = merge_sort(alist[num:])
    # 合并
    return merge(left,right)

def merge(left, right):
    '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
    #left与right的下标指针
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result

alist = [54,26,93,17,77,31,44,55,20]
sorted_alist = merge_sort(alist)
print(sorted_alist)

#时间复杂度O(nlogn)

运行结果：
[17, 20, 26, 31, 44, 54, 55, 77, 93]

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

1. 从数列中挑出一个元素，称为"基准"（pivot），
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

# 快速排序
# 思路：寻抓元素的正确位置，左边的元素都小于该元素，右边的都大于该元素
# 移动游标low，high不动则交换直到相遇(可同时交换，也可异步交换)
def quick_sort(alist,first,end):
    # 终止条件
    if first >= end:
        return
    
    
    n = len(alist)
    mid_value = alist[first]
    low = first
    high = end
    while low <high:
        # 注意处理特殊情况，遇到相等的元素放在一边处理
        while low < high and alist[high] >= mid_value:
            high -= 1
        alist[low] =alist[high]
        # low += 1
        while low < high and alist[low] < mid_value:
            low += 1
        alist[high] = alist[low]
        # high -= 1
        
    # 代码执行到此，alist[0]找到正确位置，解析来把划分出来的两段新列表递归执行
    
    alist[low] = mid_value

    # 递归部分
    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist,first,low-1)
    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist,low+1,end)


alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)
print(alist)

运行结果：[17, 20, 26, 31, 44, 54, 55, 77, 93]

多数元素

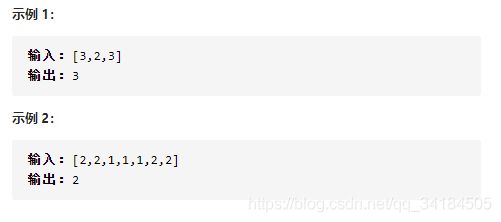
给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        # 该题分治法不是最优解，但是很好的练习
        return self.getmajrity(nums,0,len(nums)-1)
    def getmajrity(self,nums,left,right):
        # 终止条件
        if left == right:
            return nums[left]
        mid = left + (right - left) // 2
        leftmajrity = self.getmajrity(nums,left,mid)
        rightmajrity = self.getmajrity(nums,mid+1,right)

#--------------- 此处为分界线上部分为分，下部分为并----------------------

        # 当左边的多数元素 与 右边的多数元素相等时：返回其中任一值，如左边
        if leftmajrity == rightmajrity:  # 算是一个小优化(可以不要)
            return leftmajrity
        # # 如果不相等，需要分别计算左右两边，然后比较
        leftcount,rightcount = 0,0
        for i in nums[left:right+1]:   ## 这里需要+1  否则nums[right]取不到
            if i == leftmajrity:
                leftcount += 1
            elif i == rightmajrity:
                rightcount += 1

        if leftcount >= rightcount:
            return leftmajrity
        else:
            return rightmajrity 

最大子序列和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        #递归终止条件
        if n == 1:
            return nums[0]
        
        mid = len(nums) // 2
        #递归计算左半边最大子序和
        max_left = self.maxSubArray(nums[:mid])
        #递归计算右半边最大子序和
        max_right = self.maxSubArray(nums[mid:])


# -----------分界线 上面为分  下面为并----------------------------


        #计算中间的最大子序和，从右到左计算左边的最大子序和，从左到右计算右边的最大子序和，再相加
        max_l = nums[mid - 1]
        tmp = 0
        for i in range(mid - 1, -1, -1):
            tmp += nums[i]
            max_l = max(tmp, max_l)
        max_r = nums[mid]
        tmp = 0
        for i in range(mid, len(nums)):
            tmp += nums[i]
            max_r = max(tmp, max_r)
        #返回三个中的最大值
        return max(max_right,max_left,max_l+max_r)

参考资料

leetcode 官网
https://zhuanlan.zhihu.com/p/72734354