统计学极简入门——数据分布
3. 数据分布
t分布、F分布和卡方分布是统计学中常用的三种概率分布,它们分别用于样本均值的推断、方差的比较和数据的拟合优度检验。
总之这3个分布很有用,首次接触你可能理解不了,但没关系你知道很重要就行了,接着往下看,我们在介绍三大分布之前,先看一下正态分布和标准正态分布:
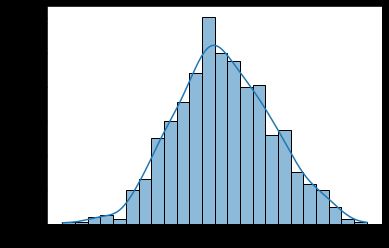
正态分布(Normal Distribution)
正态分布也被称为高斯分布,是统计学中最常见的概率分布之一。
正态分布具有钟形曲线的特征,均值和标准差是其两个重要的参数。
import numpy as np
import seaborn as sns
mean = 3 # 均值
std = 4 # 标准差
size = 1000 # 生成1000个随机数
data = np.random.normal(mean, std, size=size)
sns.histplot(data, kde=True)
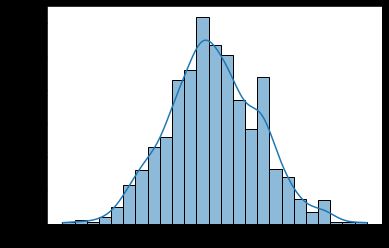
标准正态分布(Standard Normal Distribution)
标准正态分布是一种特殊的正态分布,其均值为0,标准差为1。在统计学中,标准正态分布经常用于标准化数据或进行假设检验。
import numpy as np
import seaborn as sns
size = 1000 # 生成1000个随机数
data = np.random.standard_normal(size=size)
sns.histplot(data, kde=True)
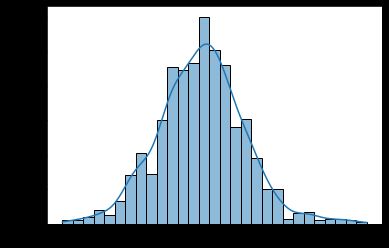
t分布(t Distribution)
t分布是一种概率分布,用于小样本情况下对总体均值的推断。当样本容量较小或总体方差未知时,使用T分布进行推断更准确。T分布的形状类似于正态分布,但尾部较宽。T分布的自由度(degrees of freedom)决定了其形状。
import numpy as np
import seaborn as sns
df = 10 # 自由度
size = 1000 # 生成1000个随机数
data = np.random.standard_t(df, size=size)
sns.histplot(data, kde=True)
F分布(F Distribution)
F分布是一种概率分布,用于比较两个样本方差的差异。F分布常用于方差分析和回归分析中。F分布的形状取决于两个自由度参数,分子自由度和分母自由度。
import numpy as np
import seaborn as sns
dfn = 5 # 分子自由度
dfd = 10 # 分母自由度
size = 1000 # 生成1000个随机数
data = np.random.f(dfn, dfd, size=size)
sns.histplot(data, kde=True)
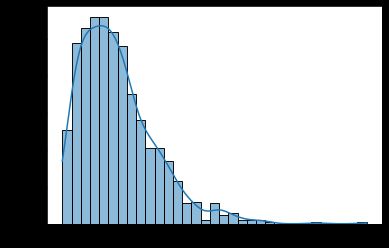
卡方分布(Chi-Square Distribution)
卡方分布是一种概率分布,用于检验观察值与理论值之间的拟合优度。卡方分布常用于拟合优度检验、独立性检验和方差分析中。卡方分布的自由度参数决定了其形状。
import numpy as np
import seaborn as sns
df = 5 # 自由度
size = 1000 # 生成1000个随机数
data = np.random.chisquare(df, size)
sns.histplot(data, kde=True)
番外篇:三大分布互相推导
注:本节作为延伸阅读,初学者简单了解即可
十九世纪中叶至二十世纪初,有三位统计学届杰出代表: 皮尔逊( Pearson) 、戈塞特( Gosset) 、费希尔( Fisher) 表,他们是统计学三大分布的始创者。
-
皮尔逊(Pearson) 在创立拟合优度理论的过程中发现了 χ 2 χ^2 χ2 分布;
-
戈塞特( Gosset) 发现 t t t 分布的过程正是 小样本理论 创立的过程;
-
费希尔( Fisher) 在创立 方差分析 理论的过程中发现了 F F F 分布。
这便是著名的三大抽样分布包括: χ 2 \chi^2 χ2 分布、 t t t 分布和 F F F 分布
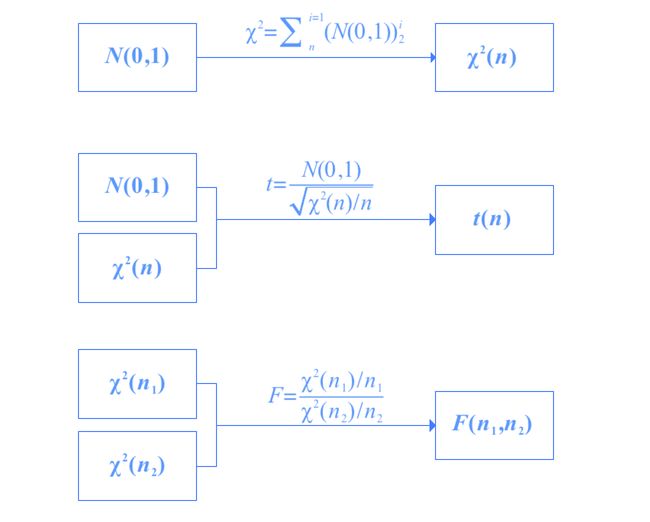
χ 2 \chi^2 χ2 分布是由 n n n个相互独立的标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1) 的平方和确定的分布,记作
χ 2 \chi^2 χ2 ~ χ 2 ( n ) χ^2(n) χ2(n) ,即
χ 2 = ∑ i = 1 n ( N ( 0 , 1 ) ) i 2 ∼ χ 2 ( n ) \chi^2=\sum_{i=1}^n(N(0,1))_i^2 \sim \chi^2(n) χ2=i=1∑n(N(0,1))i2∼χ2(n)
t t t 分布的分子是一个 N ( 0 , 1 ) N(0,1) N(0,1) ,分母是自由度为 n n n 的 χ 2 χ^2 χ2 分布与自由度 n n n的比值再开方确定的分布,记作 t t t ~ t ( n ) t(n) t(n) ,即
t = N ( 0 , 1 ) χ 2 ( n ) / n ∼ t ( n ) t=\frac{N(0,1)}{\sqrt{\chi^2(n)/n}}\sim t(n) t=χ2(n)/nN(0,1)∼t(n)
F F F 分布是由两个 χ 2 \chi^2 χ2 分布与其自由度比值的比值确定的分布 ,记 作 F F F ~ F ( n 1 , n 2 ) F (n_1,n_2) F(n1,n2) ,即
F = χ 2 ( n 1 ) / n 1 χ 2 ( n 2 ) / n 2 ∼ F ( n 1 , n 2 ) F=\frac{\chi^2\left(n_1\right) / n_1}{\chi^2\left(n_2\right) / n_2} \sim F\left(n_1, n_2\right) F=χ2(n2)/n2χ2(n1)/n1∼F(n1,n2)
三大分布的推导
三大分布的推导例题
下期预告:《Python统计学极简入门》第4节 区间估计
点击下方链接,观看下期内容。
https://edu.cda.cn/goods/show/3386