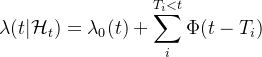Dorothy30

【笔记】社交媒体事件的Hawkes Process建模教程（2）

在上一篇笔记中，主要介绍了点过程、自激励过程以及泊松过程（最简单的点过程），参见：【笔记】社交媒体事件的Hawkes Process建模教程（1）_Dorothy30的博客-CSDN博客

在本篇笔记中，将接着上一篇笔记继续分享tutorial的第三、四部分内容，谈一谈到底什么是Hawkes Process，如何使用Hawkes Process模拟事件（两个方法）。Tutorial最后的如何估计Hawkes Process的参数和建模实例部分留到后面的笔记继续。

1. Hawkes Process的定义

2. Hawkes Process的强度函数（intensity function）详解

2.1 关于记忆核函数的选择

3 Hawkes Process的分支结构

3.1 Branching factor (branching ratio)

3.2 一个cluster里的后代总事件数量

4 模拟 Hawkes Process中的事件

4.1 The Thinning algorithm (稀疏算法)

4.1.1 齐次泊松过程的到达时间间隔采样

4.1.2 泊松过程的稀疏性质

4.1.3 使用稀疏性质的原因

4.1.4 Thinning algorithm

4.2 通过分解进行有效采样

上一篇笔记里提到过，我们在点过程中，关注的重点从一段时间内事件发生的次数转到了发生事件的间隔。在泊松过程中，事件的到达是具有无记忆性的，即过去到达的历史事件并不影响新事件的到达。而且事件到达的时间间隔可以是恒定的（ $\lambda$ 恒定，单位时间内到达的事件次数恒定），对应着齐次的泊松过程，也可以是非齐次的（单位时间内事件到达的次数随时间变化，用强度函数 $\lambda(t)$ 表示）。

在一些实际应用中，我们知道已知事件的到达会增加在不久的将来观察到事件的可能性。例如当模拟地震活动时，余震的发生，或者社交网络中用户的互动对后续交流的影响。这样的过程叫做自激励过程。

Hawkes process就是这样一类经典且应用广泛的自激励过程，即事件到达率取决于历史事件的到达情况。它由Hawkes在1971年提出。

1. Hawkes Process的定义

令 $\{N_t\}_{t>0}$ 为一个具有关联历史 $H_t(t \geq 0)$ 的计数过程。其对应的点过程由事件强度函数（intensity function） $\lambda(t|H_t)$ 表示。如果该条件强度函数的形式为下式的话，则将该点过程称为霍克斯过程（Hawkes Process）。

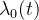$\lambda(t|\mathcal{H}_t)=\lambda_0(t)+\sum^{T_i<t}_i\Phi(t-T_i)$

$\lambda_0(t)$ : 一个确定的基础强度函数
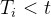: 所有在当前时间t之前发生事件的时间
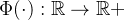$\Phi(\cdot): \mathbb{R} \rightarrow \mathbb{R}+$ 称作记忆核（ memory kernel）

当然，它也是一类特殊的非齐次泊松过程，其中事件发生的强度是随机的并且通过核函数 $\Phi(\cdot)$ 显式地依赖于先前的事件。

2. Hawkes Process的强度函数（intensity function）详解

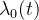intensity function由两个部分组成， $\lambda_0(t)$ 和 $\sum^{T_i<t}_i\Phi(t-T_i)$

$\lambda_0(t)$ 是基础（背景）强度，描述了由外部来源触发的事件的到来。
- 这些由外部来源触发的事件也叫外生事件或移民事件，它们的到来与过程中的先前事件无关。
$\sum^{T_i<t}_i\Phi(t-T_i)$ 是体现Hawkes process自激励的地方

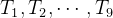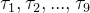Figure 1.2(a) 展示了一个Hawkes Process的实现：有九个事件在 $T_1, T_2,\cdots ,T_9$ 被观察到，这些事件对应的到达时间间隔为 $\tau_1, \tau_2,...,\tau_9$ 。

Figure 1.2(b)给出了对应的随时间变化的计数过程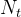，它在每个事件时间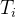增加一个单位。

Figure 1.2(c)为随时间变化的强度函数 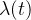$\lambda(t)$ ，从图中可以看到强度函数在每个事件发生的时候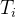（）突然上升，然后伴随着指数衰减。你也可以看到在每个衰减对于新事件强度的影响。
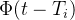- $\Phi(t-T_i)$ 用于调节过去发生在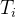时间的事件在intensity function中对于当前时间t的改变
- 通常情况下，记忆核函数 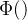$\Phi(·)$ 被认为是单调下降的，因此最近的事件对当前事件强度的影响更大

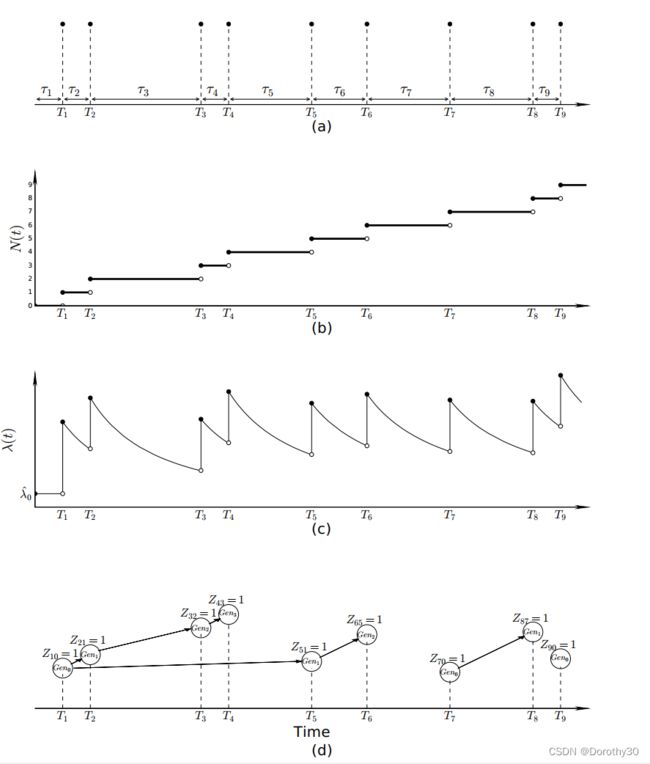Figure 1.2 带有指数衰减kernel的Hawkes Process (a)点过程示意图(b)随着时间推移的计数过程(c)随着时间推移的强度函数(d)Hawkes process的潜在的分支结构（branching structure）。标题

2.1 关于记忆核函数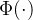 $\Phi(\cdot)$ 的选择

事实上，核函数 $\Phi(\cdot)$ 不是非要单调递减的。然而，在这个教程中，我们将仅讨论该函数是递减的情况。

一个很常见的衰减函数是指数衰减函数，采用如下形式：

$\Phi(x)=\alpha e^{-\sigma x}$

这里 $\alpha \geq0, \sigma >0$ 以及 $\alpha < \sigma$

还有一个广泛应用在各种文献里的衰减函数是power-law衰减函数：

$\Phi(x)=\frac{\alpha}{(x+\sigma)^{\eta+1}}$

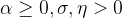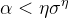
此处 $\alpha \geq0, \sigma, \eta >0$ 且 $\alpha < \eta\sigma^\eta$
这个函数经常在地震学以及社交媒体的文献中使用（因此在后面的建模实例中，我们也将使用这个形式的核函数）

3 Hawkes Process的分支结构

Hawkes Process的另一种等价形式是指泊松簇过程（Poisson cluster process），它将Hawkes process中的事件分为两个类别：移民和后代（immigrants and offspring）。其中，后代是由process中的历史事件触发的，而移民事件是独立到达的，在process中没有关联的parent event。

将后代构造成cluster，且每个cluster和与之对应的移民相关联，这称为分支结构。在这个部分的剩余内容里，将计算两个与分支内容有关的指标：branching factor（在Hawkes process里被给定事件触发的期望事件数量）和一个cluster里的后代总事件数量。

分支结构示例（Figure 1.2 d）：移民事件遵循基本强度 $\lambda_0(t)$ 的齐次泊松过程的情况，而后代是通过自激励产生的

Figure 1.2(d) 中展示了之前提到的9个事件的分支结构。事件时间用圆圈表示，“亲子”关系用箭头表示。

在这里，我们引入一个随机变量 $Z_{ij}$

当事件是移民时， $Z_{i0}= 1$

当事件是事件j的后代时， $Z_{ij} = 1$

每个圆圈里的描述了这个事件属于第几代，即属于第代，移民事件属于。

如图所示，和是移民事件的直接后代，那么在数学上可以用随机事件表示为 $Z_{10}=1, Z_{21}=1, Z_{51}=1$ 。

这种cluster的表示方式描述了一个特定的parent事件到达之后，后代如何通过非齐次泊松过程中的强度 $\Phi(\cdot)$ 与parent相关联。例如和事件的到来来自于包含有强度 $\Phi(t - T_1)$ （）的非齐次泊松过程。

产生后代的事件可以称作后代事件的直接祖先或根。例如是的直接祖先，是的直接祖先。直接或间接地与一个移民事件相连接的事件组成了后代事件的cluster。例如是移民事件，它与和形成了与相关的cluster。同样的，和自成一个cluster，自身是一个clsuter。

3.1 Branching factor (branching ratio)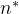

定义：由单个事件产生的直接后代的期望数量（这里的单个事件可以是祖先也可以是后代，它衡量的是一个事件的分支能力）。
- 在社交媒体的情景下，也可以将branching factor成为virality（一个帖子或消息被分享或转发的数量）
- branching factor也是判断一个与移民事件相关联的cluster是否是无限集合的指标。如果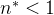，这个Hawkes Process就进入了亚临界域，代表着一个事件产生后代的能力有限，那么最终导致的cluster的规模是有界的。而当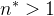时，这个Hawkes Process进入了超临界状态，这意味着每个集群中的事件总数不受限制。（如果对流行病学有所了解的话，可以将这个branching factor和基本再生数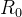联系起来，基本再生数也是一个衡量传染病传染能力的指标）
计算：branching factor的计算是通过对 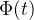$\Phi(t)$ 在事件时间 t 上的积分（每个事件的贡献）来计算：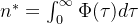

$n^*=\int_0^\infty \Phi(\tau)d\tau$
- 对这个公式的理解还要从 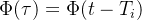$\Phi(\tau)=\Phi(t-T_i)$ 出发，前面提到这个记忆核函数是体现的每个事件发生的时间对当前时刻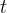事件发生的影响。 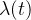$\lambda(t)$ (当前时间下，单位时间内发生事件的次数)是通过移民事件的强度与过去事件的累计影响来进行计算的，那么除去外部来源对事件到达的影响，考虑所有历史事件，就是过去历史事件可以导致的当前时间下发生事件的次数，即当前事件可以产生的后代的数量。

3.2 一个cluster里的后代总事件数量

在branching factor中，显然只有在时可以得到一个cluster里最终后代规模的更准确的估计。令为的期望事件数量，且 (在第0代只有一个事件，那就是移民事件)。那么最终在一个cluster中的期望事件总数就为 $N_\infty$ ，且按如下方式进行计算

$N_\infty = \sum_{i=0}^\infty A_i \\ = \sum_{i=0}^\infty A_{i-1}n^* \\ = \sum_{i=0}^\infty A_{i-2}(n^*)^2 \\ = \cdots \\ = \sum_{i=0}^\infty A_0(n^*)^i \\ = \sum_{i=0}^\infty(n^*)^i \\ = \frac{1}{1-n^*} \quad \text{where} \quad n < 1$

以上的计算实际上就是对前后代的事件数量建立归纳关系 $A_{i}=A_{i-1}n^*$ ，并且我们知道。所以本质上这个计算式就是等比数列求和（ $S_n=\frac{a_0 (1-q^n)}{1-q}$ ），在我们这里得到的结果应该是 $N_\infty=\frac{1-(n^*)^i}{1-n^*}$ ，然后当i趋于无穷且时， $(n^*)^i \rightarrow 0$ ，所以 $N_\infty=\frac{(1-(n^*)^i)}{1-n^*}=\frac{1}{1-n^*}$

4 模拟 Hawkes Process中的事件

我们将重点关注根据给定Hawkes process模拟一系列随机事件的问题。这将有助于收集有关过程的统计数据，并且是诊断、推理或参数估计的基础。

接下来将会介绍两种Hawkes Process的模拟方法。第一种是Thinning algorithm，适用于所有非齐次泊松过程，而且可以应用在包含任何形式的核函数 $\Phi(\cdot)$ 的Hawkes Process中。第二种方法是2013年由Dassios和Zhao提出来的，它在计算上更有效，这得益于算法设计了一个针对指数衰减kernel的Hawkes process的变量分解方法。

4.1 The Thinning algorithm (稀疏算法)

模拟Hawkes Proess的基本目标就是根据强度函数 $\lambda(t)$ 采样到达时间间隔 $\tau_i, i = 1,2,...$ 。在正式介绍对Hawkes Process的采样之前，会先回顾其次泊松过程的采样方法，在此基础上引入泊松过程的稀疏（thinning/addvitive）性质。

4.1.1 齐次泊松过程的到达时间间隔采样

在上一篇笔记中，我们提到齐次的泊松过程服从指数分布：

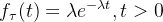
概率密度函数： $f_{\tau}(t)=\lambda e^{-\lambda t}, t>0$
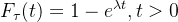
累积分布函数： $F_{\tau}(t)=1-e^{\lambda t}, t>0$

在给定参数 $\lambda$ 的情况下，我们就可以求出该过程的密度函数和累积分布函数，例如上图为 $\lambda=0.3$ 的分布情况。若想获得一系列到达时间间隔的采样点（位于x轴），我们可以根据累积分布函数（CDF）在y轴范围为[0, 1]的特点，从y轴生成服从均匀分布 $Y\sim U(0,1)$ 的n个采样点y，然后根据 $Y=F_\tau(t)$ 在CDF中通过函数的逆变换 $\tau=F_\tau^{-1}(Y)$ 求出对应在x轴的一系列n个采样点 $\tau_i$ 。这个方法称为逆变换采样。

因此，在到达时间间隔服从指数分布的泊松分布中，我们若生成一个 $u \sim U(0,1)$ ，我们有 $u=1-e^{\lambda \tau}$ ，通过变换可得 $\tau = -\frac{In(1-u)}{\lambda}$ 。由于 $(1-u) \sim U(0,1)$ ，因此对于到达时间间隔 $\tau$ 的采样可以简化为：

$Sample\ u \sim U(0,1), then\ compute\ \tau=\frac{-Inu}{\lambda}$

4.1.2 泊松过程的稀疏性质

关于泊松过程的稀疏性质，更为具体的内容可以参考这篇知乎笔记（随机过程|笔记整理（6）——泊松过程三大变换，更新过程引入 - 知乎 (zhihu.com)）。简而言之，稀疏性质就是说带有强度 $\lambda$ 的泊松过程可以被拆分为两个单独的强度为 $\lambda_1$ 和 $\lambda_2$ 过程，且 $\lambda = \lambda_1+\lambda_2$ 。换言之，原始过程中的每个事件都可以分配给独立的两个新过程之一。

利用这个稀疏性质，我们可以从一个齐次的强度 $\lambda ^* \geq \lambda(t), \forall t$ 的泊松过程中以一定概率接受/移出一部分事件，来获得强度函数为 $\lambda(t)$ 的非齐次泊松过程。

4.1.3 使用稀疏性质的原因

简单：与直接模拟具有随时间变化强度函数的非齐次过程相比，齐次泊松过程在数学上是直接的并且更容易生成。
已知属性：齐次泊松过程的统计属性已广为人知，从齐次的泊松过程开始构建使更复杂的过程会更加方便。
高效：从齐次泊松过程生成事件在计算上是高效的，并且通过稀疏性质可以保留事件的子集，这与每个时间间隔从头开始生成事件相比降低了计算复杂性。

4.1.4 Thinning algorithm

使用Thinning algorithm来模拟Hawkes process的过程如下图的伪代码所示。具体来说，就是对于任何时间间隔下的强度函数 $\lambda(t)$ ，我们都可以找到一个恒定的 $\lambda ^*$ 以满足 $\lambda^* \geq \lambda(t)$ 。那么根据带有单调下降性质核函数的Hawkes process，我们可以直观地发现对于两个连续的事件时间， $\lambda(T_i)$ 是这段到达时间间隔的强度的上界。

根据逆变换采样，我们采样得到下一个到达时间间隔 $\tau$ ，以此我们可以得到估计的下一个事件到达的时间 $T_{i+1}=T_i+\tau$ ，并计算当前的强度 $\lambda(T_{i+1})$ 。在Thinning method中，我们采用生成随机数的方式对每个事件是否到达进行基于概率的决策。也就是说我们生成一个在[0, 1]内的随机数s，并将其与 $\frac{\lambda(T)}{\lambda^*}$ (即 $\frac{\lambda_{T_{i+1}}}{\lambda_{T_i}}$ )进行比较，如果 $s \leq \frac{\lambda(T)}{\lambda^*}$ ，则接受，我们就模拟出了一个新事件的到达。否则拒绝，在 $T_{i+1}$ 没有事件到达，但时间变量仍然更新。

4.2 通过分解进行有效采样

这个由Dassios和Zhao提出的算法不需要通过概率进行接受/拒绝的判断，但它只针对于指数的移民率以及指数的记忆核函数。其中，移民率通过一个服从指数函数的非齐次泊松过程来描述： $a+(\lambda_0-a)e^{-\sigma t}$ 。对于一个新事件，它的到来对于事件强度的“跳跃”的影响是通过一个常量“ $\gamma$ ”来描述。完整的强度函数如下所示：

$\lambda(t)=a+(\lambda_0-a)e^{-\sigma t}+\sum_{T_i < t}\gamma e^{-\sigma(t-T_i)}$

值得注意的是，当记忆核函数 $\Phi(\cdot)$ 是指数形式时，由强度函数产生的过程是马尔科夫过程（Markov process）。这意味着，未来的事件发生只取决于最近的一件事情的发生，而独立于其他过去的历史事件。即，对于任意的，有 $\lambda(t_2)-a=(\lambda(t_1)-a)e^{-\sigma(t_2-t_1)}$ ，在a为常数的情况下，后一个时刻的事件的强度只取决于前一个事件的强度 $\lambda(t_1)$ 以及 $e^{-\sigma(t_2-t_1)}$ 。

因此，我们可以根据这个马尔科夫的特性把到达时间间隔分为两个简单且独立的随机变量和。

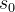：代表着下一个活动的到达时间间隔取决于恒定的background rate a
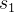：代表着下一个活动的到达时间间隔来自于指数的immigrant kernel 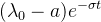$(\lambda_0-a)e^{-\sigma t}$ 或者来自于受过去事件影响的Hawkes process的自激励核函数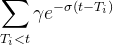 $\sum_{T_i < t}\gamma e^{-\sigma(t-T_i)}$

我们假设采样的到达间隔时间是这两种情况中的最小值。详情请参考论文：Exact simulation of Hawkes process with exponentially decaying intensity

该算法的伪代码如图所示：

算法的部分公式推导如下图：

剩下的部分留在下篇笔记继续！如果在公式推导或者理解上有不对的地方欢迎交流讨论~

关于沟通这件事，项目经理不需要每次都面对面进行流程大师兄
很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
网易严选官方旗舰店，优质商品，卓越服务高省_飞智666600
网易严选官方旗舰店是网易旗下的一家电商平台，以提供优质商品和卓越服务而闻名。作为一名SEO优化师，我将为您详细介绍网易严选官方旗舰店，并重点强调其特点和优势。大家好！我是高省APP最大团队&联合创始人飞智导师。相较于其他返利app，高省APP的佣金更高，模式更好，最重要的是，终端用户不会流失！高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
拥有断舍离的心态，过精简生活--《断舍离》读书笔记爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多，虽然摆放整齐，但也时常会觉得空间逼仄，令人心生烦闷。抱着断舍离的态度，我开始阅读《断舍离》这本书，希望从书中能找到一些有效的方法，帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的，整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”，接着又成为每个人都能实行的“改变人生的断舍离”，从“哲学”逐渐升华成“
直返最高等级与直返APP：无需邀请码的返利新体验古楼
随着互联网的普及和电商的兴起，直返模式逐渐成为一种流行的商业模式。在这种模式下，消费者通过购买产品或服务，获得一定的返利，并可以分享给更多的人。其中，直返最高等级和直返APP是直返模式中的重要概念和工具。本文将详细介绍直返最高等级的概念、直返APP的使用以及与邀请码的关系。【高省】APP（高佣金领导者）是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，运行三年，稳定可靠。高省APP，
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
数组去重好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
Day17笔记-高阶函数 ~在杰难逃~ Python 笔记 python 开发语言 pycharm 数据分析
高阶函数【重点掌握】函数的本质：函数是一个变量，函数名是一个变量名，一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数，B函数调用完成之后，会得到一个结果，则B函数被称为高阶函数常用的高阶函数：map(),reduce(),filter(),sorted()1.map()map(func,iterable)，返回值是一个iterator【容器，迭代器】func:函数iterab
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
2022现在哪个打车软件比较好用又便宜实惠的打车软件合集高省APP珊珊
这是一个信息高速传播的社会。信息可以通过手机，微信，自媒体，抖音等方式进行传播。但同时这也是一个交通四通发达的社会。高省APP，是2022年推出的平台，0投资，0风险、高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，也期待你的加入。珊珊导师，高省邀请码777777，注册送2皇冠会员，送万元推广大礼包，教你如何1年做到百万团队。高
node.js学习小猿L node.js node.js 学习 vim
node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
数据仓库——维度表一致性墨染丶eye 背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕，完整连接为：数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看，当一系列星型模型共享一组公共维度时，所涉及的维度称为一致性维度。当维度表存在不一致时，短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别，因为维度的差别，分析工作涉及的领域从简单到复杂，但是都是通过复杂的报表来弥补设计
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
【华为OD技术面试真题精选 - 非技术题】 -HR面，综合面_华为od hr面一个射手座的程序媛程序员华为od 面试职场和发展
最后的话最近很多小伙伴找我要Linux学习资料，于是我翻箱倒柜，整理了一些优质资源，涵盖视频、电子书、PPT等共享给大家！资料预览给大家整理的视频资料：给大家整理的电子书资料：如果本文对你有帮助，欢迎点赞、收藏、转发给朋友，让我有持续创作的动力！网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。需要这份系统化的资料的朋友，可以点击这里获
【Git】常见命令(仅笔记) 好想有猫猫 Git Linux学习笔记 git 笔记 elasticsearch linux c++
文章目录创建/初始化本地仓库添加本地仓库配置项提交文件查看仓库状态回退仓库查看日志分支删除文件暂存工作区代码远程仓库使用`.gitigore`文件让git不追踪一些文件标签创建/初始化本地仓库gitinit添加本地仓库配置项gitconfig-l#以列表形式显示配置项gitconfiguser.name"ljh"#配置user.namegitconfiguser.email"[email protected]
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
2022-08-28 蔚蓝一片晴
初三暑假培训收获点滴从8月25至8月27日三天两晚的培训结束了，回到家中，该静下心来整理一下触动心灵的收获，成为成长的积淀。1.在优秀团队中快速成长与提升，做一名反思成长型教师一名专业型教师的教学指导包括了教学原理知识、案例知识、策略知识。面对教学中的遇到的有趣的情形、问题会去研究其理，寻找更好的教法学法对策。从新手到成熟型教师，再走向专业型教师，需要的是觉醒与反思，多进行案例研究，从案例中观察、
为什么你总是对下属不满意? ZhaoWu1050
【ZhaoWu的听课笔记】大多数公司，都存在两种问题。我创业四年，更是体会深切。这两种问题就是：老板经常不满意下属的表现；下属总是不知道老板想要什么；虽然这两种问题普遍存在，其实解决方法并不复杂。这节课，我们再聊聊第一个问题：为什么老板经常不满意下属表现?其实，这背后也是一条管理常识。管理学家德鲁克先生早就说过：管理者的任务，不是去改变人。*来自《卓有成效的管理者》只是大多数老板和我一样，都是一边
sql统计相同项个数并按名次显示朱辉辉33 java oracle
现在有如下这样一个表： A表 ID Name time ------------------------------ 0001 aaa 2006-11-18 0002 ccc 2006-11-18 0003 eee 2006-11-18 0004 aaa 2006-11-18 0005 eee 2006-11-18 0004 aaa 2006-11-18 0002 ccc 20
Android+Jquery Mobile学习系列-目录白糖_ JQuery Mobile
最近在研究学习基于Android的移动应用开发，准备给家里人做一个应用程序用用。向公司手机移动团队咨询了下，觉得使用Android的WebView上手最快，因为WebView等于是一个内置浏览器，可以基于html页面开发，不用去学习Android自带的七七八八的控件。然后加上Jquery mobile的样式渲染和事件等，就能非常方便的做动态应用了。从现在起，往后一段时间，我打算
如何给线程池命名 daysinsun 线程池
在系统运行后，在线程快照里总是看到线程池的名字为pool-xx，这样导致很不好定位，怎么给线程池一个有意义的名字呢。参照ThreadPoolExecutor类的ThreadFactory，自己实现ThreadFactory接口，重写newThread方法即可。参考代码如下： public class Named
IE 中"HTML Parsing Error:Unable to modify the parent container element before the 周凡杨 html 解析 error readyState
错误： IE 中"HTML Parsing Error:Unable to modify the parent container element before the child element is closed" 现象：同事之间几个IE 测试情况下，有的报这个错，有的不报。经查询资料后，可归纳以下原因。
java上传 g21121 java
我们在做web项目中通常会遇到上传文件的情况，用struts等框架的会直接用的自带的标签和组件，今天说的是利用servlet来完成上传。我们这里利用到commons-fileupload组件，相关jar包可以取apache官网下载：http://commons.apache.org/ 下面是servlet的代码： //定义一个磁盘文件工厂 DiskFileItemFactory fact
SpringMVC配置学习 510888780 spring mvc
spring MVC配置详解现在主流的Web MVC框架除了Struts这个主力外，其次就是Spring MVC了，因此这也是作为一名程序员需要掌握的主流框架，框架选择多了，应对多变的需求和业务时，可实行的方案自然就多了。不过要想灵活运用Spring MVC来应对大多数的Web开发，就必须要掌握它的配置及原理。　　一、Spring MVC环境搭建：（Spring 2.5.6 + Hi
spring mvc-jfreeChart 柱图(1) 布衣凌宇 jfreechart
第一步：下载jfreeChart包，注意是jfreeChart文件lib目录下的，jcommon-1.0.23.jar和jfreechart-1.0.19.jar两个包即可；第二步：配置web.xml; web.xml代码如下 <servlet> <servlet-name>jfreechart</servlet-nam
我的spring学习笔记13-容器扩展点之PropertyPlaceholderConfigurer aijuans Spring3
PropertyPlaceholderConfigurer是个bean工厂后置处理器的实现，也就是BeanFactoryPostProcessor接口的一个实现。关于BeanFactoryPostProcessor和BeanPostProcessor类似。我会在其他地方介绍。PropertyPlaceholderConfigurer可以将上下文（配置文件）中的属性值放在另一个单独的标准java P
java 线程池使用 Runnable&Callable&Future antlove java thread Runnable callable future
1. 创建线程池 ExecutorService executorService = Executors.newCachedThreadPool(); 2. 执行一次线程，调用Runnable接口实现 Future<?> future = executorService.submit(new DefaultRunnable()); System.out.prin
XML语法元素结构的总结百合不是茶 xml 树结构
1.XML介绍1969年 gml (主要目的是要在不同的机器进行通信的数据规范)1985年 sgml standard generralized markup language1993年 html(www网)1998年 xml extensible markup language
改变eclipse编码格式 bijian1013 eclipse 编码格式
1.改变整个工作空间的编码格式改变整个工作空间的编码格式，这样以后新建的文件也是新设置的编码格式。 Eclipse->window->preferences->General->workspace-
javascript中return的设计缺陷 bijian1013 JavaScript AngularJS
代码1： <script> var gisService = (function(window) { return { name:function () { alert(1); } }; })(this); gisService.name(); &l
【持久化框架MyBatis3八】Spring集成MyBatis3 bit1129 Mybatis3
pom.xml配置 Maven的pom中主要包括： MyBatis MyBatis-Spring Spring MySQL-Connector-Java Druid applicationContext.xml配置 <?xml version="1.0" encoding="UTF-8"?> &
java web项目启动时自动加载自定义properties文件 bitray java Web 监听器相对路径
创建一个类 public class ContextInitListener implements ServletContextListener 使得该类成为一个监听器。用于监听整个容器生命周期的，主要是初始化和销毁的。类创建后要在web.xml配置文件中增加一个简单的监听器配置，即刚才我们定义的类。 <listener> <des
用nginx区分文件大小做出不同响应 ronin47
昨晚和前21v的同事聊天，说到我离职后一些技术上的更新。其中有个给某大客户(游戏下载类)的特殊需求设计，因为文件大小差距很大——估计是大版本和补丁的区别——又走的是同一个域名，而squid在响应比较大的文件时，尤其是初次下载的时候，性能比较差，所以拆成两组服务器，squid服务于较小的文件，通过pull方式从peer层获取，nginx服务于较大的文件，通过push方式由peer层分发同步。外部发布
java-67-扑克牌的顺子.从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的.2-10为数字本身，A为1，J为11，Q为12，K为13，而大 bylijinnan java
package com.ljn.base; import java.util.Arrays; import java.util.Random; public class ContinuousPoker { /** * Q67 扑克牌的顺子从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。 * 2-10为数字本身，A为1，J为1
翟鸿燊老师语录 ccii 翟鸿燊
一、国学应用智慧TAT之亮剑精神A 1. 角色就是人格就像你一回家的时候，你一进屋里面，你已经是儿子，是姑娘啦，给老爸老妈倒怀水吧，你还觉得你是老总呢？还拿派呢？就像今天一样，你们往这儿一坐，你们之间是什么，同学，是朋友。还有下属最忌讳的就是领导向他询问情况的时候，什么我不知道，我不清楚，该你知道的你凭什么不知道
[光速与宇宙]进行光速飞行的一些问题 comsci 问题
在人类整体进入宇宙时代，即将开展深空宇宙探索之前，我有几个猜想想告诉大家仅仅是猜想。。。未经官方证实 1：要在宇宙中进行光速飞行，必须首先获得宇宙中的航行通行证，而这个航行通行证并不是我们平常认为的那种带钢印的证书，是什么呢？下面我来告诉
oracle undo解析 cwqcwqmax9 oracle
oracle undo解析2012-09-24 09:02:01 我来说两句作者：虫师收藏我要投稿 Undo是干嘛用的？ &nb
java中各种集合的详细介绍 dashuaifu java 集合
一，java中各种集合的关系图 Collection 接口的接口对象的集合 ├ List 子接口 &n
卸载windows服务的方法 dcj3sjt126com windows service
卸载Windows服务的方法在Windows中，有一类程序称为服务，在操作系统内核加载完成后就开始加载。这里程序往往运行在操作系统的底层，因此资源占用比较大、执行效率比较高，比较有代表性的就是杀毒软件。但是一旦因为特殊原因不能正确卸载这些程序了，其加载在Windows内的服务就不容易删除了。即便是删除注册表中的相应项目，虽然不启动了，但是系统中仍然存在此项服务，只是没有加载而已。如果安装其他
Warning: The Copy Bundle Resources build phase contains this target's Info.plist dcj3sjt126com ios xcode
http://developer.apple.com/iphone/library/qa/qa2009/qa1649.html Excerpt: You are getting this warning because you probably added your Info.plist file to your Copy Bundle
2014之C++学习笔记（一） Etwo C++Etwo Etwo iterator 迭代器
已经有很长一段时间没有写博客了，可能大家已经淡忘了Etwo这个人的存在，这一年多以来，本人从事了AS的相关开发工作，但最近一段时间，AS在天朝的没落，相信有很多码农也都清楚，现在的页游基本上达到饱和，手机上的游戏基本被unity3D与cocos占据，AS基本没有容身之处。so。。。最近我并不打算直接转型
js跨越获取数据问题记录 haifengwuch jsonp json Ajax
js的跨越问题，普通的ajax无法获取服务器返回的值。第一种解决方案，通过getson，后台配合方式，实现。 Java后台代码： protected void doPost(HttpServletRequest req, HttpServletResponse resp) throws ServletException, IOException { String ca
蓝色jQuery导航条 ini JavaScript html jquery Web html5
效果体验：http://keleyi.com/keleyi/phtml/jqtexiao/39.htmHTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>jQuery鼠标悬停上下滑动导航条 - 柯乐义<
linux部署jdk,tomcat,mysql kerryg jdk tomcat linux mysql
1、安装java环境jdk: 一般系统都会默认自带的JDK,但是不太好用，都会卸载了，然后重新安装。 1.1）、卸载：（rpm -qa :查询已经安装哪些软件包； rmp -q 软件包：查询指定包是否已
DOMContentLoaded VS onload VS onreadystatechange mutongwu jquery js
1. DOMContentLoaded 在页面html、script、style加载完毕即可触发，无需等待所有资源（image/iframe）加载完毕。（IE9+） 2. onload是最早支持的事件，要求所有资源加载完毕触发。 3. onreadystatechange 开始在IE引入，后来其它浏览器也有一定的实现。涉及以下 document , applet, embed, fra
sql批量插入数据 qifeifei 批量插入
hi，自己在做工程的时候，遇到批量插入数据的数据修复场景。我的思路是在插入前准备一个临时表，临时表的整理就看当时的选择条件了，临时表就是要插入的数据集，最后再批量插入到数据库中。 WITH tempT AS ( SELECT item_id AS combo_id, item_id, now() AS create_date FROM a
log4j打印日志文件如何实现相对路径到项目工程下 thinkfreer Web log4j 应用服务器日志
最近为了实现统计一个网站的访问量，记录用户的登录信息，以方便站长实时了解自己网站的访问情况，选择了Apache 的log4j,但是在选择相对路径那块卡主了，X度了好多方法(其实大多都是一样的内用，还一个字都不差的)，都没有能解决问题，无奈搞了2天终于解决了，与大家分享一下需求：用户登录该网站时，把用户的登录名,ip,时间。统计到一个txt文档里，以方便其他系统调用此txt。项目名
linux下mysql-5.6.23.tar.gz安装与配置笑我痴狂 mysql linux unix
1.卸载系统默认的mysql [root@localhost ~]# rpm -qa | grep mysql mysql-libs-5.1.66-2.el6_3.x86_64 mysql-devel-5.1.66-2.el6_3.x86_64 mysql-5.1.66-2.el6_3.x86_64 [root@localhost ~]# rpm -e mysql-libs-5.1

【笔记】社交媒体事件的Hawkes Process建模教程（2）

1. Hawkes Process的定义

2. Hawkes Process的强度函数（intensity function）详解

2.1 关于记忆核函数的选择

3 Hawkes Process的分支结构

3.1 Branching factor (branching ratio)

3.2 一个cluster里的后代总事件数量

4 模拟 Hawkes Process中的事件

4.1 The Thinning algorithm (稀疏算法)

4.1.1 齐次泊松过程的到达时间间隔采样

4.1.2 泊松过程的稀疏性质

4.1.3 使用稀疏性质的原因

4.1.4 Thinning algorithm

4.2 通过分解进行有效采样

你可能感兴趣的:(Hawkes,Process,学习笔记,自用整理,笔记,算法,概率论,数学建模)

2.1 关于记忆核函数 $\Phi(\cdot)$ 的选择