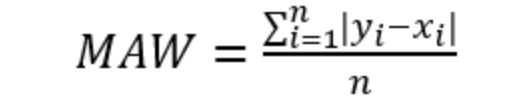用于时间序列预测的最佳深度学习模型总结
来源:数据STUDIO
本文约6700字,建议阅读11分钟
本文讨论了5种专门研究时间序列预测的深度学习体系结构。时间序列预测在最近两年内发生了巨大的变化,尤其是在kaiming的MAE出现以后,现在时间序列的模型也可以用类似MAE的方法进行无监督的预训练。
Makridakis M-Competitions系列(分别称为M4和M5)分别在2018年和2020年举办(M6也在今年举办了)。对于那些不了解的人来说,m系列得比赛可以被认为是时间序列生态系统的一种现有状态的总结,为当前得预测的理论和实践提供了经验和客观的证据。
2018年M4的结果表明,纯粹的“ ML”方法在很大程度上胜过传统的统计方法,这在当时是出乎意料的。在两年后的M5[1]中,最的高分是仅具有“ ML”方法。并且所有前50名基本上都是基于ML的(大部分是树型模型)。这场比赛看到了LightGBM(用于时间序列预测)以及Amazon's Deepar [2]和N-Beats [3]的首次亮相。N-Beats模型于2020年发布,并且优于M4比赛的获胜者3%!
最近的 Ventilator Pressure Prediction比赛展示了使用深度学习方法来应对实时时间序列挑战的重要性。比赛的目的是预测机械肺内压力的时间顺序。每个训练实例都是自己的时间序列,因此任务是一个多个时间序列的问题。获胜团队提交了多层深度架构,其中包括LSTM网络和Transformer 块。
在过去的几年中,许多著名的架构已经发布,如MQRNN和DSSM。所有这些模型都利用深度学习为时间序列预测领域贡献了许多新东西。除了赢得Kaggle比赛,还给我们带来了更多的进步比如:
多功能性:将模型用于不同任务的能力。
MLOP:在生产中使用模型的能力。
解释性和解释性:黑盒模型并不那么受欢迎。
本文讨论了5种专门研究时间序列预测的深度学习体系结构,论文是:
N-BEATS (ElementAI)
DeepAR (Amazon)
Spacetimeformer [4]
Temporal Fusion Transformer or TFT (Google) [5]
TSFormer(时间序列中的MAE)[7]
N-BEATS
这种模式直接来自于(不幸的)短命的ElementAI公司,该公司是由Yoshua Bengio联合创立的。顶层架构及其主要组件如图1所示:
N-BEATS是一个纯粹的深度学习架构,它基于集成前馈网络的深度堆栈,这些网络也通过正向和反向的相互连接进行堆叠。
每一个块只对由前一个的backcast产生的残差进行建模,然后基于该误差更新预测。该过程模拟了拟合ARIMA模型时的Box-Jenkins方法。
以下是该模型的主要优势:
表达性强且易于使用:该模型易于理解,具有模块化结构,它被设计为需要最小的时间序列特征工程并且不需要对输入进行缩放。
该模型具有对多个时间序列进行概括的能力。换句话说,分布略有不同的不同时间序列可以用作输入。在N-BEATS中是通过元学习实现的。元学习过程包括两个过程:内部学习过程和外部学习过程。内部学习过程发生在块内部,并帮助模型捕获局部时间特征。外部学习过程发生在堆叠层,帮助模型学习所有时间序列的全局特征。
双重残差叠加:残差连接和叠加的想法是非常巧妙的,它几乎被用于每一种类型的深度神经网络。在N-BEATS的实现中应用了相同的原理,但有一些额外的修改:每个块有两个残差分支,一个运行在回看窗口(称为backcast),另一个运行在预测窗口(称为forecast)。
每一个连续的块只对由前一个块重建的backcast产生的残差进行建模,然后基于该误差更新预测。这有助于模型更好地逼近有用的后推信号,同时最终的堆栈预测预测被建模为所有部分预测的分层和。就是这个过程模拟了ARIMA模型的Box-Jenkins方法。
可解释性:模型有两种变体,通用的和可解释性的。在通用变体中,网络任意学习每个块的全连接层的最终权值。在可解释的变体中,每个块的最后一层被删除。然后将后推backcast和预测forecast分支乘以模拟趋势(单调函数)和季节性(周期性循环函数)的特定矩阵。
注意:原始的N-BEATS实现只适用于单变量时间序列。
DeepAR
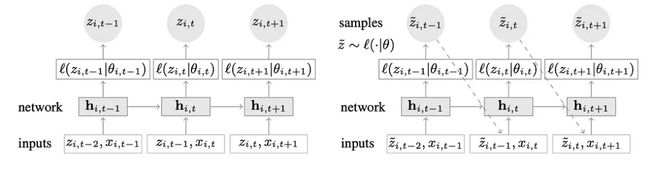
结合深度学习和自回归特性的新颖时间序列模型。图2显示了DeepAR的顶层架构:
以下是该模型的主要优势:
DeepAR在多个时间序列上工作得非常好:通过使用多个分布略有不同的时间序列来构建全局模型。也适用于许多现实场景。例如电力公司可能希望为每个客户推出电力预测服务,每个客户都有不同的消费模式(这意味着不同的分布)。
除了历史数据,DeepAR还允许使用已知的未来时间序列(自回归模型的一个特点)和额外的静态属性。在前面提到的电力需求预测场景中,一个额外的时间变量可以是月份(作为一个整数,值在1-12之间)。假设每个客户都与一个测量功耗的传感器相关联,那么额外的静态变量将是sensor_id或customer_id之类的东西。
如果莫熟悉使用MLPs和rnn等神经网络架构进行时间序列预测,那么一个关键的预处理步骤是使用标准化或标准化技术对时间序列进行缩放。这在DeepAR中是不需要手动操作的,因为底层的模型对每个时间序列i的自回归输入z进行缩放,缩放因子为v_i,即该时间序列的平均值。具体而言,论文基准中使用的比例因子方程如下:
但是在实践中,如果目标时间序列的大小差异很大,那么在预处理过程中应用自己的缩放还是很有必要的。例如,在能源需求预测场景中,数据集可以包含中压电力客户(例如小工厂,按兆瓦单位消耗电力)和低压客户(例如家庭,按千瓦单位消耗电力)。
DeepAR进行概率预测,而不是直接输出未来值。这是以蒙特卡洛样本的形式完成的。这些预测被用来计算分位数预测,通过使用分位数损失函数。对于那些不熟悉这种损失类型的人,分位数损失不仅用来计算一个估计,而且用来计算围绕该值的预测区间。
Spacetimeformer
在单变量时间序列中时间依赖性是最重要的。但是在多个时间序列场景中,事情就没那么简单了。例如假设我们有一个天气预报任务,想要预测五个城市的温度。让我们假设这些城市属于一个国家。鉴于目前所看到的,我们可以使用DeepAR并将每个城市作为外部静态协变量进行建模。
换句话说,该模型将同时考虑时间和空间关系。这便是Spacetimeformer的核心理念:使用一个模型来利用这些城市/地点之间的空间关系,从而学习额外的有用依赖,因为模型将同时考虑时间和空间关系。
深入研究时空序列
顾名思义,这种模型在内部使用了基于transformers的结构。在使用基于transformers的模型进行时间序列预测时,一种流行的产生时间感知嵌入的技术是通过Time2Vec[6]嵌入层传递输入(对于NLP任务是使用位置编码向量来代替Time2Vec)。虽然这种技术对于单变量时间序列非常有效,但对于多变量时间输入却没有任何意义。可能是在语言建模中,句子中的每个单词都用嵌入表示,单词本质上是一个是词汇表的一部分,而时间序列则没那么简单。
在多元时间序列中,在给定的时间步长t,输入的形式为x_1,t, x2,t, x_m,t其中x_i,t是特征i的数值,m是特征/序列的总数。如果我们将输入通过一个Time2Vec层,将产生一个时间嵌入向量。这种嵌入真正代表什么?答案是它将把整个输入集合表示为单个实体(令牌)。因此模型将只学习时间步之间的时间动态,但将错过特征/变量之间的空间关系。
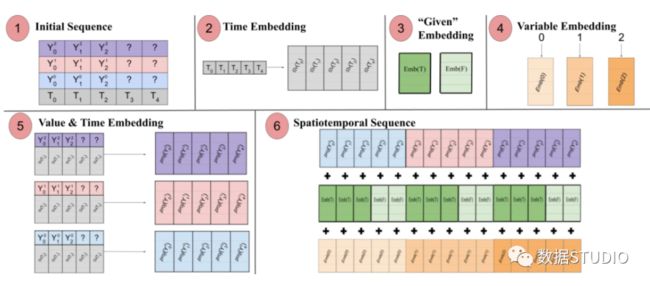
Spacetimeformer解决了这个问题,它将输入扁平化为一个大向量,称为时空序列。如果输入包含N个变量,组织成T个时间步,则生成的时空序列将具有(NxT)标记。下图3更好地显示了这一点:
论文指出:“(1)包含时间信息的多元输入格式。解码器输入缺少(“?”)值,在进行预测时设置为零。(2)时间序列通过一个Time2Vec层,生成一个代表周期性输入模式的频率嵌入。(3)二进制嵌入表示该值是作为上下文给出的还是需要预测的。(4)将每个时间序列的整数索引映射到一个具有查找表嵌入的“空间”表示。(5)利用前馈层投影每个时间序列的Time2Vec嵌入和变量值。(6)将值和时间,变量和给定的嵌入求和会导致使MSA在时间和可变空间之间以更长的序列作为输入。
换句话说,最后的序列编码了一个包含了时间、空间和上下文信息统一的嵌入。但是这种方法的一个缺点是,序列可能会变得很长导致资源的二次增长。这是因为根据注意机制,每个令牌都要对另一个进行检查。作者使用了一种更有效的体系结构,称为Performer注意机制,适用于更大的序列。
Temporal Fusion Transformer
Temporal Fusion Transformer(TFT)是由Google发布的基于Transformer的时间序列预测模型。TFT比以前的模型更加通用。
TFT的顶层架构如图4所示。以下是该模型的主要优势:
与前面提到的模型一样,TFT支持在多个异构时间序列上构建模型。
TFT支持三种类型的特征:i)具有已知的未来输入的时变数据ii)仅到目前为止已知的时变数据iii)分类/静态变量,也被称为时不变特征。因此TFT比以前的型号更通用。在前面提到的电力需求预测场景中,我们希望使用湿度水平作为一个时变特征,这是到目前为止才知道的。这在TFT中是可行的,但在DeepAR中不行。
图5显示了如何使用所有这些特性的示例:

TFT非常强调可解释性。具体地说,通过利用Variable Selection组件(如上图4所示),模型可以成功地度量每个特性的影响。因此可以说模型学习了特性的重要性。
另一方面,TFT提出了一种新的可解释的多头注意机制:该层的注意权重可以揭示在回顾期间哪些时间步是最重要的。这些权重的可视化可以揭示整个数据集中最显著的季节模式。
预测区间:与DeepAR类似,TFT通过使用分位数回归输出预测区间和预测值。
综上所述,深度学习无疑彻底改变了时间序列预测的格局。上述所有模型除了无与伦比的性能之外,还有一个共同点:它们充分利用多重、多元的时间数据,同时它们使用外生信息,将预测性能提高到前所未有的水平。但是在自然语言处理(NLP)任务中多数都利用了预训练的模型。NLP任务的feed大多是人类创造的数据,充满了丰富而优秀的信息,几乎可以看作是一个数据单元。在时间序列预测中,我们可以感觉到缺乏这种预先训练的模型。为什么我们不能像在NLP中那样在时间序列中利用这个优势呢?
这就引出了我们要介绍的最后一个模型TSFormer,该模型考虑了两个视角,我们讲从输入到输出将其为四个部分,并且提供Python的实现代码(官方也提供了),这个模型是刚刚发布不久的,所以我们才在这里着重介绍它。
TSFormer
它是一种基于Transformer(TSFormer)的无监督的时间序列预训练模型,使用了MAE中的训练策略并且能够捕获数据中非常长的依赖关系。
NLP和时间序列:
在某种程度上,NLP信息和Time Series数据是相同的。它们都是顺序数据和局部敏感的,这意味着与它的下一个/以前的数据点有关。但是还是有一些区别,在提出我们的预训练模型时,我们应该考虑两个差异,就像我们在NLP任务中所做的那样:
时间序列数据的密度比自然语言数据低得多
我们需要比NLP数据更长的时间序列数据
TSFormer简介
TSFormer与MAE的主要体系结构基本类似,数据通过一个编码器,然后经过一个解码器,最终的目标是为了重建缺失(人工掩蔽)的数据。
我们将他总结为以下4点
1、掩蔽
作为数据进入编码器的前一步。输入序列(Sᶦ)已分布到P片中,其长度为L。因此,用于预测下一个时间步长的滑动窗口的langth是P XL。
遮蔽比率为75%(看着很高,估计是用了MAE一样的参数);我们要完成的是一项自监督任务,所以数据越少编码器的计算速度就越快。
这样做(掩蔽输入序列段)的主要原因是:
段(patch)比单独点好。
它使使用下游模型变得简单(STGNN将单元段作为输入)
可以分解编码器的输入大小。
class Patch(nn.Module):
def __init__(self, patch_size, input_channel, output_channel, spectral=True):
super().__init__()
self.output_channel = output_channel
self.P = patch_size
self.input_channel = input_channel
self.output_channel = output_channel
self.spectral = spectral
if spectral:
self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)
else:
self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))
def forward(self, input):
B, N, C, L = input.shape
if self.spectral:
spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)
real = spec_feat_.real
imag = spec_feat_.imag
spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)
output = self.emb_layer(spec_feat).transpose(-1, -2)
else:
input = input.unsqueeze(-1) # B, N, C, L, 1
input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1
output = self.input_embedding(input) # B*N, d, L/P, 1
output = output.squeeze(-1).view(B, N, self.output_channel, -1)
assert output.shape[-1] == L / self.P
return output以下是生成遮蔽的函数
class MaskGenerator(nn.Module):
def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):
super().__init__()
self.mask_size = mask_size
self.mask_ratio = mask_ratio
self.sort = True
self.average_patch = lm
self.distribution = distribution
if self.distribution == "geom":
assert lm != -1
assert distribution in ['geom', 'uniform']
def uniform_rand(self):
mask = list(range(int(self.mask_size)))
random.shuffle(mask)
mask_len = int(self.mask_size * self.mask_ratio)
self.masked_tokens = mask[:mask_len]
self.unmasked_tokens = mask[mask_len:]
if self.sort:
self.masked_tokens = sorted(self.masked_tokens)
self.unmasked_tokens = sorted(self.unmasked_tokens)
return self.unmasked_tokens, self.masked_tokens
def geometric_rand(self):
mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked
self.masked_tokens = np.where(mask)[0].tolist()
self.unmasked_tokens = np.where(~mask)[0].tolist()
# assert len(self.masked_tokens) > len(self.unmasked_tokens)
return self.unmasked_tokens, self.masked_tokens
def forward(self):
if self.distribution == 'geom':
self.unmasked_tokens, self.masked_tokens = self.geometric_rand()
elif self.distribution == 'uniform':
self.unmasked_tokens, self.masked_tokens = self.uniform_rand()
else:
raise Exception("ERROR")
return self.unmasked_tokens, self.masked_tokens2、编码
包括了输入嵌入,位置编码和Transformer 块的。编码器只能在未遮蔽的patchs上执行(这个也是MAE的方法)。
输入嵌入
使用线性的投影来获得输入的嵌入,可将未遮蔽的空间转换为潜在空间。它的公式可以在下面看到:
W和B是可学习的参数,U是维度中的模型输入向量。
位置编码
简单的位置编码层用于附加新的顺序信息。添加了“可学习”一词,这有助于表现出比正弦更好的性能。因此可学习的位置嵌入显示了时间序列的良好结果。
class LearnableTemporalPositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len: int = 1000):
super().__init__()
self.dropout = nn.Dropout(p=dropout)
self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)
nn.init.uniform_(self.pe, -0.02, 0.02)
def forward(self, X, index):
if index is None:
pe = self.pe[:X.size(1), :].unsqueeze(0)
else:
pe = self.pe[index].unsqueeze(0)
X = X + pe
X = self.dropout(X)
return X
class PositionalEncoding(nn.Module):
def __init__(self, hidden_dim, dropout=0.1):
super().__init__()
self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)
def forward(self, input, index=None, abs_idx=None):
B, N, L_P, d = input.shape
# temporal embedding
input = self.tem_pe(input.view(B*N, L_P, d), index=index)
input = input.view(B, N, L_P, d)
# absolute positional embedding
return inputTransformer 块
论文使用了4层Transformer ,比计算机视觉和自然语言处理任务中常见的数量低。这里所使用的Transformer 是最基本的也是在原始论文中提到的结构,如下图4所示:
class TransformerLayers(nn.Module):
def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):
super().__init__()
self.d_model = hidden_dim
encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)
self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)
def forward(self, src):
B, N, L, D = src.shape
src = src * math.sqrt(self.d_model)
src = src.view(B*N, L, D)
src = src.transpose(0, 1)
output = self.transformer_encoder(src, mask=None)
output = output.transpose(0, 1).view(B, N, L, D)
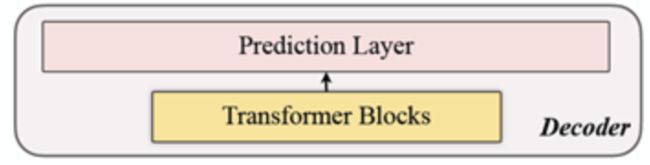
return output3、解码
该解码器包括一系列Transformer块。它适用于所有的patch(相比之下MAE是没有位置嵌入,因为他的patch已经有位置信息),并且层数只有一层,然后使用了简单的MLP,这使得输出长度等于每个patch的长度。
4、重建目标
对每一个数据点(i)进行遮蔽patch的计算,并选择mae (Mean-Absolute-Error)作为主序列和重建序列的损失函数。
这就是整体的架构了
下面是代码实现:
def trunc_normal_(tensor, mean=0., std=1.):
__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)
def unshuffle(shuffled_tokens):
dic = {}
for k, v, in enumerate(shuffled_tokens):
dic[v] = k
unshuffle_index = []
for i in range(len(shuffled_tokens)):
unshuffle_index.append(dic[i])
return unshuffle_index
class TSFormer(nn.Module):
def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):
super().__init__()
self.patch_size = patch_size
self.seleted_feature = selected_feature
self.mode = mode
self.spectral = spectral
self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)
self.pe = PositionalEncoding(out_channel, dropout=dropout)
self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)
self.encoder = TransformerLayers(out_channel, L)
self.decoder = TransformerLayers(out_channel, 1)
self.encoder_2_decoder = nn.Linear(out_channel, out_channel)
self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))
trunc_normal_(self.mask_token, std=.02)
if self.spectral:
self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)
else:
self.output_layer = nn.Linear(out_channel, patch_size)
def _forward_pretrain(self, input):
B, N, C, L = input.shape
# get patches and exec input embedding
patches = self.patch(input)
patches = patches.transpose(-1, -2)
# positional embedding
patches = self.pe(patches)
# mask tokens
unmasked_token_index, masked_token_index = self.mask()
encoder_input = patches[:, :, unmasked_token_index, :]
# encoder
H = self.encoder(encoder_input)
# encoder to decoder
H = self.encoder_2_decoder(H)
# decoder
# H_unmasked = self.pe(H, index=unmasked_token_index)
H_unmasked = H
H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)
H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d
H = self.decoder(H_full)
# output layer
if self.spectral:
# output = H
spec_feat_H_ = self.output_layer(H)
real = spec_feat_H_[..., :int(self.patch_size/2+1)]
imag = spec_feat_H_[..., int(self.patch_size/2+1):]
spec_feat_H = torch.complex(real, imag)
out_full = torch.fft.irfft(spec_feat_H)
else:
out_full = self.output_layer(H)
# prepare loss
B, N, _, _ = out_full.shape
out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]
out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)
label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P
label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()
label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)
# prepare plot
## note that the output_full and label_full are not aligned. The out_full in shuffled
### therefore, unshuffle for plot
unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)
out_full_unshuffled = out_full[:, :, unshuffled_index, :]
plot_args = {}
plot_args['out_full_unshuffled'] = out_full_unshuffled
plot_args['label_full'] = label_full
plot_args['unmasked_token_index'] = unmasked_token_index
plot_args['masked_token_index'] = masked_token_index
return out_masked_tokens, label_masked_tokens, plot_args
def _forward_backend(self, input):
B, N, C, L = input.shape
# get patches and exec input embedding
patches = self.patch(input)
patches = patches.transpose(-1, -2)
# positional embedding
patches = self.pe(patches)
encoder_input = patches # no mask when running the backend.
# encoder
H = self.encoder(encoder_input)
return H
def forward(self, input_data):
if self.mode == 'Pretrain':
return self._forward_pretrain(input_data)
else:
return self._forward_backend(input_data)看完这个论文,我发现这基本上可以说是复制了MAE,或者说是时间序列的MAE,在预测阶段也是与MAE类似,使用编码器的输出作为特征,为下游任务提供特征数据作为输入,有兴趣的可以读读原始论文并且看看论文给的代码。
参考
[1] Makridakis et al., The M5 Accuracy competition: Results, findings and conclusions, (2020)
[2] D. Salinas et al., DeepAR: Probabilistic forecasting with autoregressive recurrent networks, International Journal of Forecasting (2019).
[3] Boris N. et al., N-BEATS: Neural Basis Expansion Analysis For Interpretable Time Series Forecasting, ICLR (2020)
[4] Jake Grigsby et al., Long-Range Transformers for Dynamic Spatiotemporal Forecasting,
[5] Bryan Lim et al., Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting, International Journal of Forecasting September 2020
[6] Seyed Mehran Kazemi et al.,Time2Vec: Learning a Vector Representation of Time, July 2019
[7] Pre-training Enhanced Spatial-temporal Graph Neural Network for Multivariate Time Series Forecasting
[8] Masked Autoencoders Are Scalable Vision Learners
编辑:于腾凯
校对:林亦霖