2015 ICPC 沈阳站M题
M - Meeting
Time Limit:6000MS Memory Limit:262144KB 64bit IO Format:%I64d & %I64u
Submit Status Practice HDU 5521
Appoint description: System Crawler (2016-04-18)
Description
Bessie and her friend Elsie decide to have a meeting. However, after Farmer John decorated his
fences they were separated into different blocks. John's farm are divided into 
blocks labelled from 
to .
Bessie lives in the first block while Elsie lives in the -th one. They have a map of the farm
which shows that it takes they 
minutes to travel from a block in to another block
in where 
is a set of blocks. They want to know how soon they can meet each other
and which block should be chosen to have the meeting.
Input
The first line contains an integer 
, the number of test cases. Then test cases
follow.
The first line of input contains and . 
. The following lines describe the sets . Each line will contain two integers 
and 
firstly. Then integer follows which are the labels of blocks in . It is guaranteed that 
.
Output
For each test case, if they cannot have the meeting, then output "Evil John" (without quotes) in one line.
Otherwise, output two lines. The first line contains an integer, the time it takes for they to meet.
The second line contains the numbers of blocks where they meet. If there are multiple
optional blocks, output all of them in ascending order.
Sample Input
2 5 4 1 3 1 2 3 2 2 3 4 10 2 1 5 3 3 3 4 5 3 1 1 2 1 2
Sample Output
Case #1: 3 3 4 Case #2: Evil John
Hint
In the first case, it will take Bessie 1 minute travelling to the 3rd block, and it will take Elsie 3 minutes travelling to the 3rd block. It will take Bessie 3 minutes travelling to the 4th block, and it will take Elsie 3 minutes travelling to the 4th block. In the second case, it is impossible for them to meet.
题意
有 N个点 n<=100000 ,m《=10000个集合，在同一个集合中的人意两个点的距离都相等，不同的集合时间不一定相同， 一个人从1 出发，一个人从n出发求 二人相遇的最时间
思路：
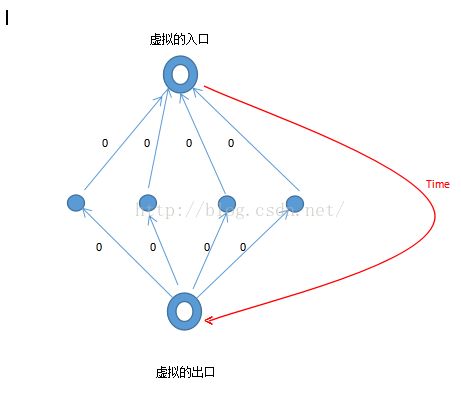
如果按普通的写法 则需要建立很多的边，边太多是存不下的，所以要缩图，缩图的方法
这样就可以了 ，保证了集合内的点人意点都是time 哈
但是 使用普通的SPFA 就会超时！！QAQ
需要是用 dijktra + 优先队列
套了个最短路优化模版 就可以了
#include
#include
#include
#include
#include
#include
#define pb push_back
#define mp make_pair
#define sz(x) ((int)(x).size())
using namespace std;
const int N = 1000100*2;
const long long INF = 1e18;
int n, m;
long long dis[N];
long long dis1[N];
long long dis2[N];
long long f[N];
bool vis[N];
struct Node
{
long long d;
int e;
bool operator < (const Node x) const
{
return x.d < d;
}
Node(long long d, int e):d(d), e(e) {}
};
vector > V[N];
void dijkstra(int s)
{
priority_queue q;
fill(dis + 1, dis + n+2*m + 1, INF);
fill(vis + 1, vis + n+2*m + 1, false);
q.push(Node(0, s));
dis[s] = 0;
while(!q.empty())
{
Node deq = q.top();
q.pop();
if(vis[deq.e])
continue;
vis[deq.e] = true;
for(int i = 0; i < sz(V[deq.e]); i++)
{
int e = V[deq.e][i].first;
long long w = V[deq.e][i].second;
if(dis[deq.e] < dis[e] - w)
{
dis[e] = dis[deq.e] + w;
q.push(Node(dis[e], e));
}
}
}
}
void add_edge(int a,int b,long long c)
{
V[a].push_back(make_pair(b, c));
}
long long max(long long a,long long b)
{
if(a>b)
return a;
return b;
}
long long min(long long a,long long b)
{
if(a>b)return b;
return a;
}
int main()
{
int T;
scanf("%d",&T);
int CASE=1 ;
while(T--)
{
scanf("%d%d",&n,&m);
int fc = n+1;
for(int i = 1; i<=n+m*2+1; i++)
V[i].clear();
long long time ;
int y;
for(int i = 1; i<=m; i++)
{
scanf("%lld%d",&time,&y);
int temp ;
for(int j = 1; j<=y; j++)
{
scanf("%d",&temp);
add_edge(temp,fc,0);
add_edge(fc+1,temp,0);
}
add_edge(fc,fc+1,time);
fc+=2;
}
dijkstra(1);
memcpy(dis1,dis,sizeof(dis));
dijkstra(n);
memcpy(dis2,dis,sizeof(dis));
long long minv = INF;
for(int i =1 ; i<=n; i++)
{
f[i] = max(dis1[i],dis2[i]);
minv = min(minv,f[i]);
}
printf("Case #%d: ",CASE++);
if(minv>=INF)
{
printf("Evil John\n");
}
else
{
printf("%lld\n",minv);
int flagc = 0;
for(int i = 1; i<=n; i++)
{
if(f[i]==minv)
{
if(!flagc)
{
printf("%d",i);
flagc = 1;
}
else
printf(" %d",i);
}
}
printf("\n");
}
}
return 0;
}