基础算法--归并排序

归并排序

归并，先递归，后合并。归并排序（Merge Sort）是建立在归并操作上的一种排序算法。其主要思想是分而治之。

若将两个有序集合并成一个有序表，称为2-路归并，与之对应的还有多路归并。

怎么分

对于排序最好的情况来讲，就是只有两个元素，这时候比较大小就很简单，但是还是需要比较
如果拆分为左右各一个，无需比较，左右各一个，每一个单独即是有序的。

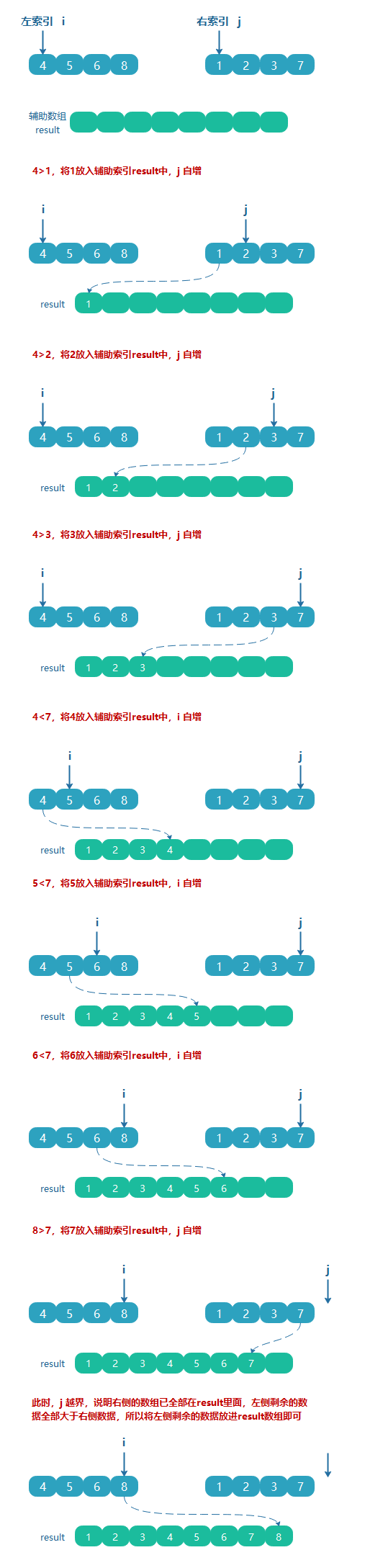
怎么治

借助一个辅助空数组，把左右两边的数组按照大小比较，按顺序放入辅助数组中即可。

算法稳定性理解

合二为一也是归并排序的难点。其实也是一个双指针算法。
当左右指针遇到相同的两个数字，取左右哪一个都可以。
一般情况下是把第一个数字移到后面去，因为这样这样是稳定。
稳定是指原序列中两个值是相同的，在排完序之后，他们的位置如果不发生变化，那么这个排序就是稳定的。
他们的位置可能发生变化的话，那么这个排序就是不稳定的。这个没什么卵用，只是考试可能考到。

以下面两个有序数组为例：

代码实现

acwing C++代码模板:

#include 
using namespace std;

const int N = 1000010;
int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    	if(q[i] <= q[j]) tmp[k ++] = q[i ++];
    	else tmp[k ++] = q[j ++];
    
    while(i <= mid) tmp[k ++] = q[i ++];
    while(j <= r) tmp[k ++] = q[j ++];
    
    for(i = l, j = 0; i <= r; i ++, j ++) q[i] = tmp[j];
    
    
}


int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++) scanf("%d", &q[i]);
        
    merge_sort(q, 0, n - 1);
    
    for(int i = 0; i < n; i++) printf("%d ", q[i]);
    
    return 0;
}

python代码实现：

import random
import sys

# 最大递归深度
sys.setrecursionlimit(10 ** 6)


def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1

    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1

    li[low:high + 1] = ltmp


def merge_sort(li, low, high):
    if low < high:
        mid = (low + high) // 2
        # 分左边
        merge_sort(li, low, mid)  # 闭区间
        # 分右边
        merge_sort(li, mid + 1, high)

        # 合并
        merge(li, low, mid, high)


li = [i for i in range(100)]
random.shuffle(li)
print(li)
merge_sort(li, 0, len(li) - 1)
print(li)

时间复杂度

归并排序方法就是把一组n个数的序列，折半分为两个序列，然后再将这两个序列再分，一直分下去，直到分为n个长度为1的序列。然后两两按大小归并。如此反复，直到最后形成包含n个数的一个数组。

归并排序总时间 = 分解时间 + 子序列排好序时间 + 合并时间

无论每个序列有多少数都是折中分解，所以分解时间是个常数，可以忽略不计，则：

归并排序总时间 = 子序列排好序时间 + 合并时间

假设处理的数据规模大小为 n，运行时间设为：T(n)，则T(n) = n，当 n = 1时，T(1) = 1

由于在合并时，两个子序列已经排好序，所以在合并的时候只需要 if 判断即可，所以n个数比较，合并的时间复杂度为 n。

将 n 个数的序列，分为两个 n/2 的序列，则：T(n) = 2T(n/2) + n
将 n/2 个数的序列，分为四个 n/4 的序列，则：T(n) = 4T(n/4) + 2n
将 n/4 个数的序列，分为八个 n/8 的序列，则：T(n) = 8T(n/8) + 3n
…
将 n/2k 个数的序列，分为2k个 n/2k 的序列，则：T(n) = 2kT(n/2k) + kn
当 T(n/2k) = T(1)时， 即n/2k = 1（此时也是把n分解到只有1个数据的时候），转换为以2为底n的对数：k = log2n，把k带入到T(n)中，得：T(n) = n + nlog2n。

使用大O表示法，去掉常数项 n，省略底数 2，则归并排序的时间复杂度为：O(nlogn)

算法稳定性

从原理分析和代码可以看出，为在合并的时候，如果相等，选择前面的元素到辅助数组，所以归并排序是稳定