【算法系列篇】分治-归并
文章目录
- 前言
- 什么是归并算法
- 1. 排序数组
-
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 数组中逆序对
-
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3. 计算右侧小于当前元素的个数
-
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 翻转对
-
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 总结
前言
上一篇算法文章,我们介绍了分治-快排的算法,今天我将为大家分享关于分治的另外一种算法——归并。
什么是归并算法
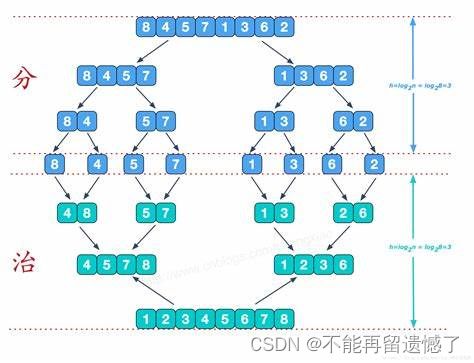
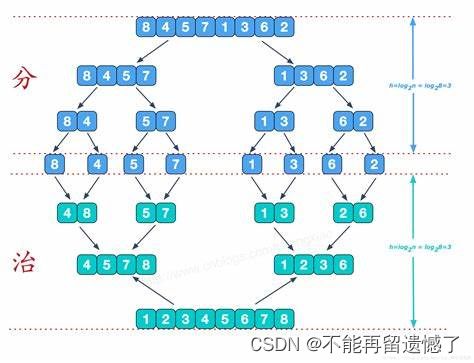
归并算法是一种常用的排序算法,它采用分治策略将待排序的数组分解为更小的子数组,然后逐步合并这些子数组以获得最终的有序数组。归并排序的主要思想是将两个有序的子数组合并成一个有序的数组。
归并算法通常包含以下步骤:
-
分解(Divide):将待排序的数组递归地分解为规模更小的子数组,直到每个子数组只有一个元素或为空。
-
解决(Conquer):通过递归地排序子数组,将其转化为有序的子数组。这通常是通过继续将子数组进一步分解并排序的方式实现的。
-
合并(Merge):将两个有序的子数组合并成一个有序的数组。该步骤的实现方式是比较两个子数组的元素,并按照顺序合并到一个新的数组中,直到所有元素都被合并。
归并排序的时间复杂度是O(nlogn),其中n是待排序数组的长度。它的主要优点包括:
-
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序不会被改变。
-
适用性:归并排序适用于各种数据结构,尤其在外部排序中,它对于大规模数据的排序效果明显。
然而,归并排序也存在一些缺点:
-
额外空间消耗:归并排序需要额外的空间来存储临时的子数组和合并结果,这可能对内存消耗造成一定影响。
-
递归调用:归并排序的实现通常使用递归调用,对于大规模数据的排序可能导致递归深度增加,从而增加了额外的函数调用开销。
总结而言,归并排序是一种高效、稳定的排序算法,通过分治策略将待排序的数组分解为更小的子数组,然后逐步合并这些子数组以获得最终的有序数组。尽管归并排序需要额外的空间和函数调用开销,但它在实践中被广泛使用,特别适用于对大规模数据进行排序。
1. 排序数组
https://leetcode.cn/problems/sort-an-array/
1.1 题目要求
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
- 1 <= nums.length <= 5 * 104
- -5 * 104 <= nums[i] <= 5 * 104
class Solution {
public int[] sortArray(int[] nums) {
}
}
1.2 做题思路
不知道大家是否做过将两个有序数组合并为一个有序数组,我们的归并算法就是通过将两个数组合并为一个有序数组来实现的。而归并的思想就是就一整个数组从中间将数组分为两个数组,然后再继续将这两个数组分别从中间分开,直到将这两部分的数组分为只有一个元素的两部分数组,然后将这两个数组通过合并两个数组的操作来进行合并,合并完成之后的数组就成为了一个有序的数组,然后继续将这两个有序的数组通过合并数组的操作继续进行合并,直到将这些数组合并为一个最大的数组。
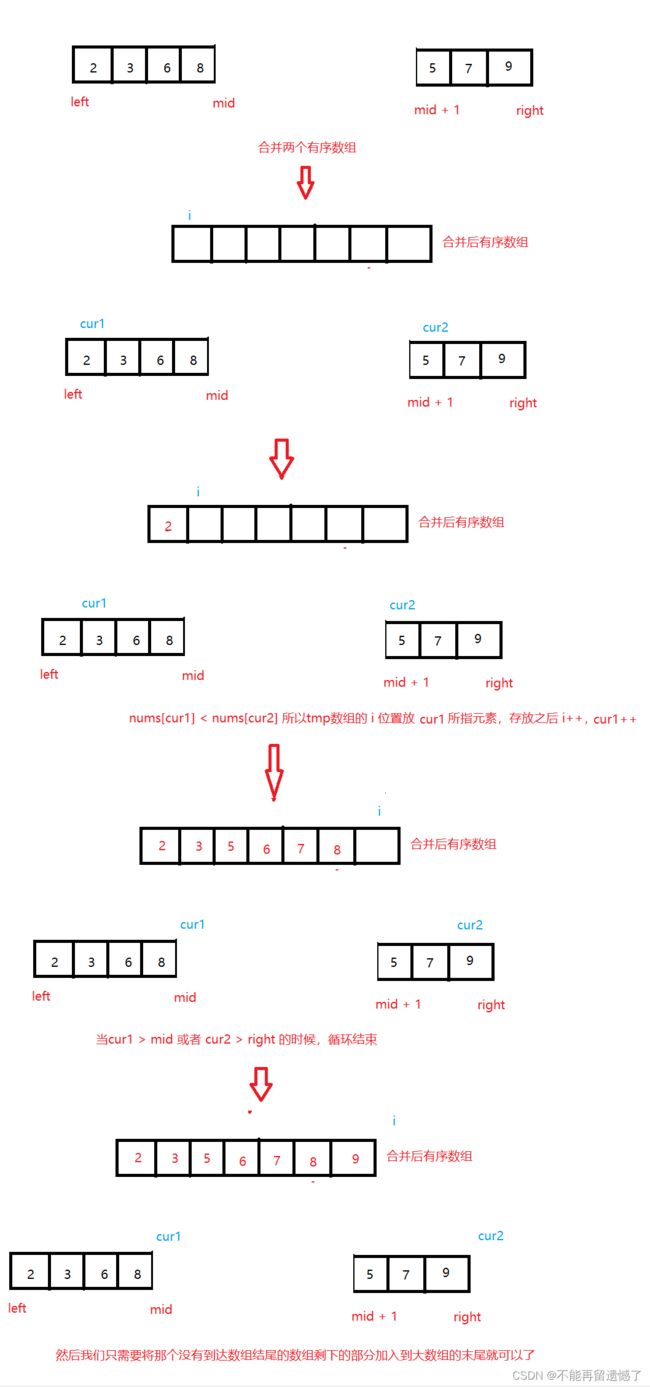
1.3 Java代码实现
class Solution {
//因为每一次递归都需要创建临时的数组来存储两个数组排序之后的结果,
//每次都向申请内存,速度会很慢
//所以我们直接申请一个跟nums同样大小的数组
int[] tmp;
public int[] sortArray(int[] nums) {
int n = nums.length;
tmp = new int[n];
mergeSort(nums,0,n -1);
return nums;
}
private void mergeSort(int[] nums, int left, int right) {
//当数组中只有一个元素或者区间不成立的时候,结束递归
if(left >= right) return;
int mid = left + (right - left) / 2;
//先排序mid左右两边的数组,最后在将左右两边的有序数组进行合并
mergeSort(nums,left,mid);
mergeSort(nums,mid + 1,right);
int cur1 = left,cur2 = mid + 1,i = 0;
while(cur1 <= mid && cur2 <= right) {
tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];
}
//处理没到达数组结尾的数组
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
//将临时排序之后数组的结果更新到我们原本的数组中
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
}
}
2. 数组中逆序对
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
2.1 题目要求
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
限制:
- 0 <= 数组长度 <= 50000
class Solution {
public int reversePairs(int[] nums) {
}
}
2.2 做题思路
我们先来看看如何使用暴力解法来解决这个问题:用两层循环来遍历数组,i 从 0 开始,j 则从 i 的下一个位置开始,看 j 所指向的位置是否小于 i 所指的位置,如果是则逆序对总数加一。这样虽然简单,但是时间复杂度达到了 O(N^2),是跑不过去的,那么我们就需要对暴力解法进行优化,问题就在于我们该如何优化呢?
这样想,如果我们将数组分为两个部分,先计算左边部分的数组中的所有逆序对,然后计算右边部分数组中的所有逆序对,最后在左边数组一次选择一个数字,看右边数组中是否元素能与左边数组中的那个元素构成逆序对,这样的思路其实跟暴力解法是相同的,时间复杂度都是 O(N^2),那么当我们分别在左边数组中和右边数组中找到了符合的逆序对的话,我们是否可以将这两部分数组进行排序呢?当进行了排序之后,再分别在左边数组中依次拿元素与右边数组中的元素进行比较,假设我们按照升序的方式进行排序,当左边部分遇到比右边数组部分大的元素的话,那么左边数组部分从这个元素开始到左边部分数组结束的位置是否都大于右边数组的该元素呢?
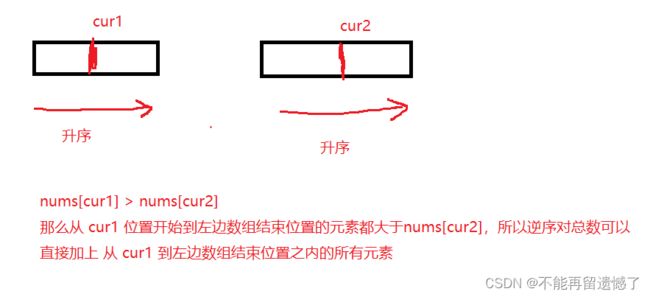
如果nums[cur1] < nums[cur2] 则继续让 cur1 向右移动,直到出现逆序对的情况,这样 cur1 和 cur2 指针都不用返回,就较少了很多的重复比较,使得时间复杂度提升为
O(N*logN)。
2.3 Java代码实现
(1)升序方法
class Solution {
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums,0,n-1);
}
private int mergeSort(int[] nums, int left, int right) {
if(left >= right) return 0;
int mid = left + (right - left) / 2;
//统计逆序对的数量
int ret = 0;
//计算左边数组中逆序对的数量
ret += mergeSort(nums,left,mid);
//计算右边数组中逆序对的数量
ret += mergeSort(nums,mid + 1,right);
int cur1 = left, cur2 = mid + 1,i = 0;
while(cur1 <= mid && cur2 <= right) {
//当nums[cur1] <= nums[cur2] 的时候,只需要进行合并数组的操作
if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur1++];
//当nums[cur1] > nums[cur2] 的时候,需要更新逆序对的数量,同时也需要合并数组
else {
ret += mid - cur1 + 1;
tmp[i++] = nums[cur2++];
}
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
return ret;
}
}
(2)降序方法
我们也可以用降序排列的方式来实现归并排序,只是当使用降序的时候,需要在右边数组中统计逆序对的数量,因为当遇到 nums[cur1] > nums[cur2] 的时候,如果还是统计左边数组 mid - cur1 + 1 作为逆序对的数量的话,那么当 cur2 向后移动的时候,再遇到 nums[cur1] > nums[cur2] 的时候就会出现重复的情况,所以当我们以降序的方式排序的时候需要在右边数组中统计逆序对的数量。
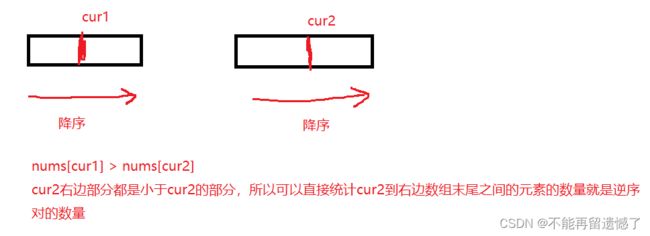
class Solution {
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums,0,n-1);
}
private int mergeSort(int[] nums, int left, int right) {
if(left >= right) return 0;
int mid = left + (right - left) / 2;
//统计逆序对的数量
int ret = 0;
//计算左边数组中逆序对的数量
ret += mergeSort(nums,left,mid);
//计算右边数组中逆序对的数量
ret += mergeSort(nums,mid + 1,right);
int cur1 = left, cur2 = mid + 1,i = 0;
while(cur1 <= mid && cur2 <= right) {
//当nums[cur1] <= nums[cur2] 的时候,只需要进行合并数组的操作
if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur2++];
//当nums[cur1] > nums[cur2] 的时候,需要更新逆序对的数量,同时也需要合并数组
else {
ret += right - cur2 + 1;
tmp[i++] = nums[cur1++];
}
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
return ret;
}
}
3. 计算右侧小于当前元素的个数
https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/
3.1 题目要求
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1,-1]
输出:[0,0]
提示:
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
class Solution {
public List<Integer> countSmaller(int[] nums) {
}
}
3.2 做题思路
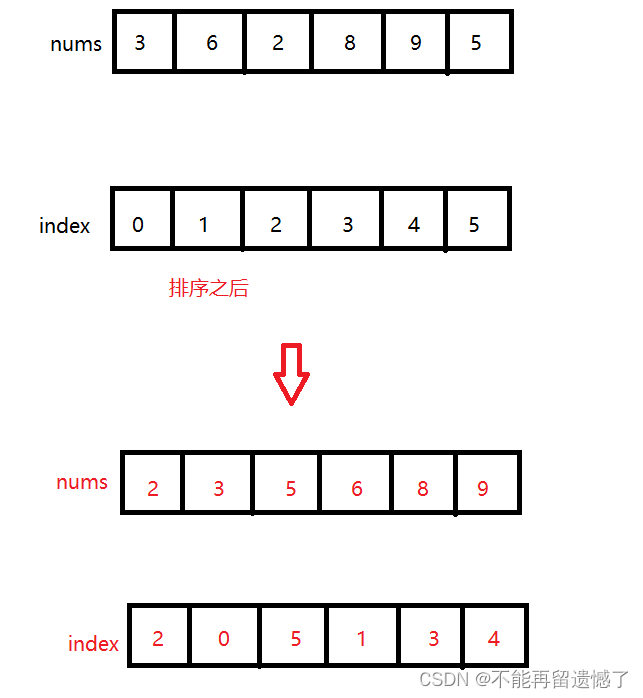
这道题目跟上面的找逆序对的数量是类似的,逆序对是找前面的元素大于后面元素的个数,而这道题是需要找到数组中每个元素的之后的小于该元素的个数,也就是说这个题目返回的是多个数,而不是一个数。那么我们在使用分冶算法的过程中该如何记住对应数字的下标呢?因为在分冶的过程中加上排序,数组中元素的位置是不断变化的,但是这道题目按顺序返回数组中对用位置右边部分大小小于该位置元素的数量,所以这道题目如何记住原本数组对应元素的下标是很重要的。
那么我们如何记住原本数组元素的对应下标呢?我们可以创建一个 index 数组,当数组进行合并排序的时候,相应的 index 数组也跟着变化,这样就能使排序后数组对应位置的 index 数组中存放的是原本数组的下标。
3.3 Java代码实现
class Solution {
int[] ret; //该数组中存放右侧小于当前元素的个数
int[] index; //存放对应元素的下标
int[] tmpNums; //排序后的临时数组
int[] tmpIndex; //排序后对应元素的原本下标
public List<Integer> countSmaller(int[] nums) {
int n = nums.length;
ret = new int[n];
index = new int[n];
//index 数组初始化
for(int i = 0; i < n; i++) index[i] = i;
tmpNums = new int[n];
tmpIndex = new int[n];
mergerSort(nums,0,n-1);
List<Integer> list = new ArrayList<>();
for(int x : ret) list.add(x);
return list;
}
private void mergerSort(int[] nums, int left, int right) {
if(left >= right) return;
int mid = left + (right - left) / 2;
mergerSort(nums,left,mid);
mergerSort(nums,mid + 1,right);
int cur1 = left, cur2 = mid + 1, i = 0;
//降序
while(cur1 <= mid && cur2 <= right) {
if(nums[cur1] <= nums[cur2]) {
tmpNums[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
}else {
//因为前面的递归中可能出现了右侧小于当前位置的数,所以需要使用+=
ret[index[cur1]] += right - cur2 + 1;
tmpNums[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
}
while(cur1 <= mid) {
tmpNums[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
while(cur2 <= right) {
tmpNums[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
}
for(int j = left; j <= right; j++) {
nums[j] = tmpNums[j - left];
index[j] = tmpIndex[j - left];
}
}
}
4. 翻转对
https://leetcode.cn/problems/reverse-pairs/description/
4.1 题目要求
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1]
输出: 2
示例 2:
输入: [2,4,3,5,1]
输出: 3
注意:
- 给定数组的长度不会超过50000。
- 输入数组中的所有数字都在32位整数的表示范围内。
class Solution {
public int reversePairs(int[] nums) {
}
}
4.2 做题思路
这个题目跟前面的的两个题目都是类似的,只是这里不能在我们更新翻转对的时候就进行排序,因为翻转对的判断条件是 i < j 且 nums[i] > 2*nums[j],根据这个判断条件,我们不能判断出 nums[i] 和 nums[j] 哪个大,所以只能在更新完翻转对之后进行归并排序,其他的步骤基本上是类似的。
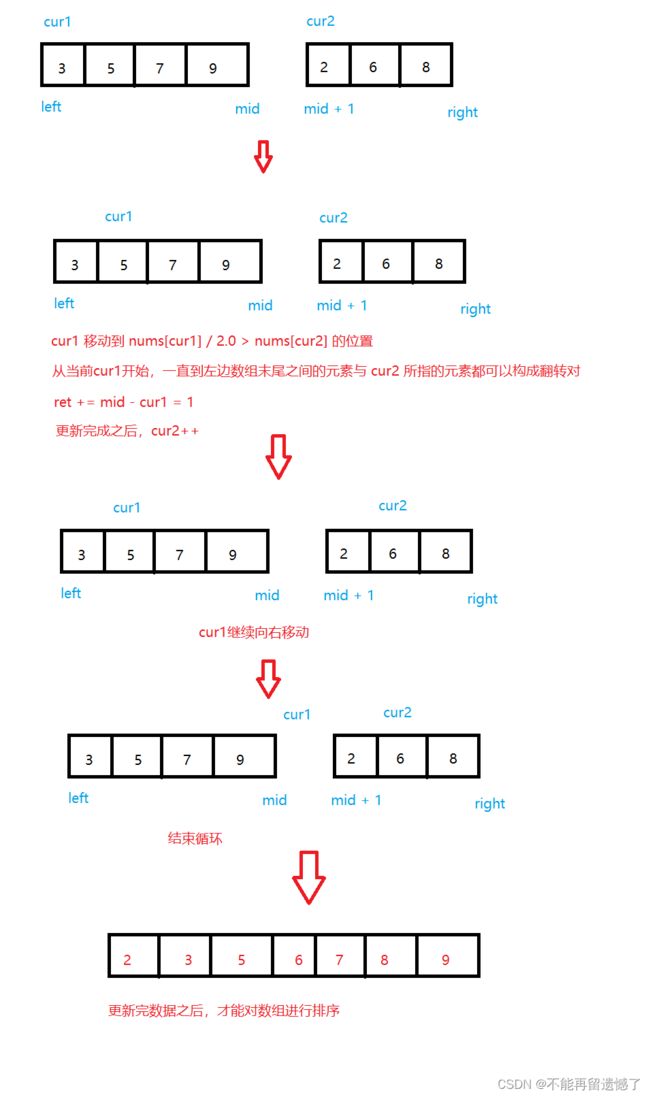
4.3 Java代码实现
(1)升序
class Solution {
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums,0,n-1);
}
private int mergeSort(int[] nums, int left, int right) {
if(left >= right) return 0;
int ret = 0;
int mid = left + (right - left) / 2;
//统计左右两部分数组中翻转对的数量
ret += mergeSort(nums,left,mid);
ret += mergeSort(nums,mid + 1,right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur2 <= right) {
//这里需要使用nums[cur1] / 2.0 而不是nums[cur2] * 2,
//因为可能会导致溢出
while(cur1 <= mid && nums[cur1] / 2.0 <= nums[cur2]) cur1++;
if(cur1 > mid) break;
ret += mid - cur1 + 1;
cur2++;
}
//升序
cur1 = left;
cur2 = mid + 1;
while(cur1 <= mid && cur2 <= right) {
tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
return ret;
}
}
(2)降序
class Solution {
int[] tmp;
public int reversePairs(int[] nums) {
int n = nums.length;
tmp = new int[n];
return mergeSort(nums,0,n-1);
}
private int mergeSort(int[] nums, int left, int right) {
if(left >= right) return 0;
int ret = 0;
int mid = left + (right - left) / 2;
ret += mergeSort(nums,left,mid);
ret += mergeSort(nums,mid + 1,right);
int cur1 = left, cur2 = mid + 1, i = 0;
//降序
while(cur1 <= mid) {
//这里cur1不动,因为cur1向后移动只会越来越小,所以让cur2向后移动
while(cur2 <= right && nums[cur1] / 2.0 <= nums[cur2]) cur2++;
if(cur2 > right) break;
ret += right - cur2 + 1;
cur1++;
}
cur1 = left;
cur2 = mid + 1;
while(cur1 <= mid && cur2 <= right) {
tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++] : nums[cur1++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
return ret;
}
}
总结
归并排序是一种高效而稳定的排序算法,它利用了分治策略,将待排序的数组分解为更小的子数组,并逐步合并这些子数组以获得最终的有序数组。
归并排序算法的核心思想是将待排序数组递归地分解为规模更小、有序的子数组,然后通过合并操作将这些子数组有序地合并成一个大的有序数组。这种分解和合并的过程直到最终合并成排序后的完整数组。
归并排序算法具有以下优点:
-
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序不会被改变。这使得它特别适用于对具有多关键字排序要求的情况。
-
高效性:归并排序的时间复杂度为O(nlogn),其中n是待排序数组的长度。它具有较好的性能表现,并适用于大规模数据的排序。
此外,归并排序算法还具有一定的弹性和灵活性。它可以通过优化合并操作的实现方式,减少额外空间的消耗。此外,归并排序也适用于外部排序,可以处理存储在外部存储介质中的大规模数据。
尽管归并排序算法需要额外的空间和函数调用开销,但由于其稳定性和较好的时间复杂度,它在实际应用中被广泛采用。