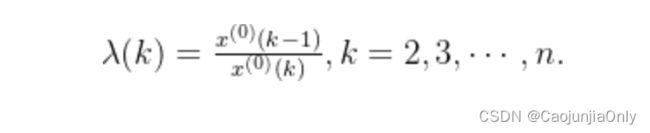【数学建模竞赛】预测类赛题常用算法解析

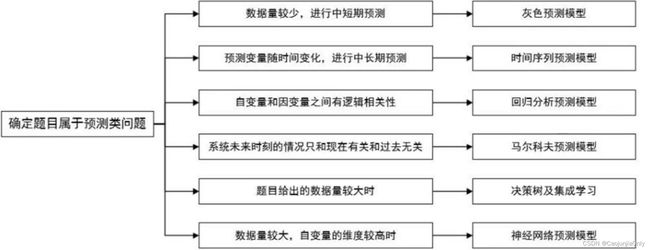
解析常见的预测类算法

灰色预测模型

灰色预测模型是一种利用少量的、不完全的信息，建立数学模型并进行预测的方法。该方法通过对系统行为特征的发展变化规律进行估计预测，同时也可以对行为特征的异常情况发生的时刻进行估计计算，并研究特定时间区间内事件的未来时间分布情况。灰色预测主要使用灰色系统理论中的GM(1,1)模型进行处理。该模型在工业、农业、商业等经济领域，以及环境、社会和军事等领域中都有广泛的应用。它可以根据已有的数据对未来的发展趋势进行预测分析，具有较高的精度和可靠性。

级比检验

级比检验是用来判断原始数据是否满足准指数规律的一种方法。

在灰色预测中，首先需要对原始数据进行级比检验。

级比公式如下，X0表示原始数据。

级比检验的目的是判断数据是否满足准指数规律。 

在级比检验中，首先需要计算级比，即原始数据与其前一期数据的比值。然后对级比进行统计分析，如计算平均值、方差等。根据级比的统计结果，可以判断数据是否满足准指数规律。如果级比的绝对值接近1，则说明数据满足准指数规律；如果级比的绝对值远离1，则说明数据不满足准指数规律。 级比检验是灰色预测中一个重要的步骤，它可以帮助我们判断数据是否适合进行灰色预测分析。根据级比检验的结果，我们可以选择合适的灰色预测模型进行预测。 

x=input('请输入数据');
n=length(x);
jibi = ones(1,n-1);
for i = 2:n
jibi(i-1) = x(i-1)/x(i);
end
max1 = max(jibi);
min1 = min(jibi);
fanwei = exp(2/(n+2))-exp(-2/(n+1))
if max1 - min1 

灰色预测过程 

1.首先生成累加数列。

2.再通过加权邻值生成等权邻值生成数。

3.通过推导可知我们生成的等权邻值生成数满足一定的指数规律，我们的目标就是求出下列灰微分方程中a,b的值：

4.得到灰微分方程后我们就可以对数据进行预测了。

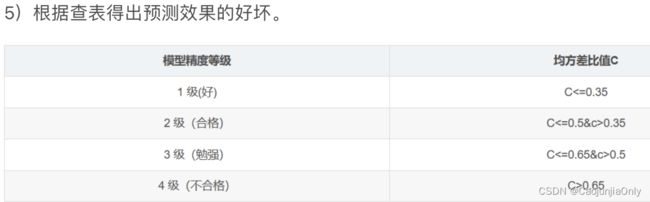
5.最后进行检验，本文用了两种常见的检验方式。

x=input('请输入数据');%x表示原数据
n=length(x);
x1 = ones(1,n);
x1(1)=x(1);
%%生成一次累加数列
for i=2:n
x1(i)=x1(i-1)+x(i)% x1表示累加后的数据
end
z=ones(n-1,2);
%%加权生成数列z
for i=1:(n-1)
z(i,1)=-(x1(i)+x1(i+1))/2;
z(i,2)=1;
end
B=z';
for i=1:(n-1)
x0(i)=x(i+1);%x0表示初始数据的2-n项
end
x0=x0';
U=inv(B*z)*B*x0;
a=U(1);
b=U(2);
t=b/a;
t_test=input('输入需要预测的个数');
i=1:t_test+n;
yucezhi1(i+1)=(x(1)-t).*exp(-a.*i)+t;
yucezhi1(1)=x(1);
yucezhi0 = x(1);
for j=n+t_test:-1:2
yucezhi0(j)=yucezhi1(j)-yucezhi1(j-1);
end
x_init = x;
x=1:n;
xs=2:n+t_test;
yn=yucezhi0(2:n+t_test);
plot(x,x,'^r',xs,yn,'*-b');
% det=0;
% for i=2:n
% det=det+abs(yn(i)-x(i));
% end
% det=det/(n-1);
% disp(['百分绝对误差为：',num2str(det),'%']);
x0 = x0';
%%进行普通的残差检验
for i = 1:n
cancha0(i) = abs((x_init(i)-yucezhi0(i))/x_init(i));
end
cancha_max = max(cancha0);
if cancha_max<0.1
disp(['数据达到较高的要求'])
elseif cancha_max<0.2
disp(['数据达到一般的要求'])
else
disp(['数据不满足要求'])
end
%%进行后验差检验
cancha1(i) = (x_init(i)-yucezhi0(i));
s1 = 0;
s2 = 0;
x_average = sum(x_init)/n;
e_average = sum(cancha1)/n;
for i = i:n
s1 = s1+(x_init(i)-x_average)^2;
s2 = s2+(cancha1(i)-e_average)^2;
end
s1 = s1/n;
s2 = s2/n;
C = s2/s1;
if C<=0.35
disp(['一级，效果好']);
elseif C<=0.5 &C>0.35
disp(['二级，合格']);
elseif C<=0.65 &C>0.5
disp(['三级，勉强']);
else
disp(['四级，不合格']);
end
disp(['预测值为：',num2str(yucezhi0(n+1:n+t_test))]);

回归预测方法

回归预测方法包括线性回归、逻辑回归以及其他常见的回归模型。线性回归和逻辑回归通常是人们学习预测模型的第一个算法，而了解更多的学者会知道它们只是所有回归模型的主要两种形式。事实上，回归模型有很多种形式，每种回归都有其特定的适用场合。

在实际应用中，我们可以根据具体需求选择合适的回归模型。除了线性回归和逻辑回归，还有其他常见的回归模型，如多项式回归、岭回归、Lasso回归、弹性网络回归、决策树回归以及随机森林回归等。逐步回归是一种常见的逐步拟合回归模型的方法，通过观察统计值和指标来辨别重要的变量，并逐步增加或删除协变量来优化回归模型。对于有创造力的人来说，也可以根据需要对回归参数进行组合或创造出新的回归模型。但在实际应用中，我们通常会使用最常见的几种回归模型来进行预测和分析。

 时间序列分析法

时间序列分析法是一种通过对时间序列中的观察值进行描述和分析来预测未来值或理解序列中的模式和趋势的方法。根据时间序列的不同观察时间，可以是年份、季度、月份或其他任何时间形式。这种方法可以帮助我们了解序列中的趋势、季节性、周期性以及其他可能的影响因素。传统的时间序列分析方法可以将序列中的各个成分分离出来，并通过数学关系式进行分析。这样可以更好地理解序列中的成分之间的关系，并帮助我们做出合理的预测。 时间序列分析法具有简洁、实用的特点，对于利用人力、物力、财力、资源等方面的决策和规划具有很大的帮助。

ARIMA模型 

ARIMA模型是一种用于时间序列分析和预测的经典模型。它是由自回归(AR)、移动平均(MA)和差分(I)组成的。ARIMA模型可以用来分析具有一定趋势和季节性的时间序列数据。AR模型是指自回归模型，它用过去观测值的线性组合来预测未来观测值。MA模型是指移动平均模型，它使用白噪声误差的线性组合来预测未来观测值。ARIMA模型可以使用AR、MA或I模型的组合来进行模型配置，以便适应特定的时间序列数据模式。

如果想了解更详细的ARIMA模型的具体内容，可以参考Duke大学的网站，他们提供了关于ARIMA模型的详细解释和应用示例。

在ARIMA模型中，参数值为0可以用来表示不使用该模型的某个部分。这意味着ARIMA模型可以被配置为执行ARMA模型的功能，甚至是简单的AR、I或MA模型。

一旦我们得到了一个平稳的时间序列，下一步就是选择合适的ARIMA模型，也就是模式识别。这一步一般涉及对数据进行模型拟合和参数估计，以及用信息准则来选择最佳模型。通过这些步骤，我们可以得到一个适合时间序列数据的ARIMA模型，从而进行进一步的分析和预测。

AR - 自回归

自回归模型，顾名思义，就是及时地“回顾”过去，分析数据中先前的值，并对它们做出假设。这些先前的值称为“滞后”。一个例子是显示每月铅笔销售的数据。每个月的销售总额将被认为是数据集中的一个“进化变量”。这个模型是作为“利益的演化变量根据其自身的滞后值(即先验值)进行回归”而建立的。

I - 表示综合

与类似的“ARMA”模型相反，ARIMA中的“I”指的是它的综合方面。当应用差分步骤时，数据是“综合”的，以消除非平稳性。表示原始观测值的差异，以允许时间序列变得平稳，即数据值被数据值和以前的值之间的差异替换。

MA - 移动平均线

该模型的移动平均方面，是将观测值与应用于滞后观测值的移动平均模型的残差之间的相关性合并。

ARIMA用于使模型尽可能地符合时间序列数据的特殊形式。

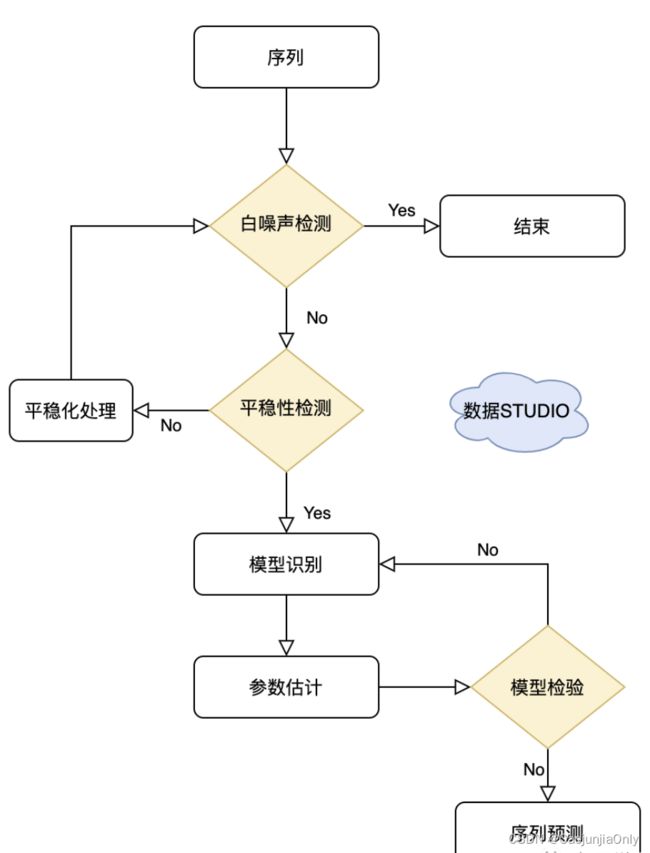
一般步骤

① 首先需要对观测值序列进行平稳性检测，如果不平稳，则对其进行差分运算直到差分后的数据平稳；
② 在数据平稳后则对其进行白噪声检验，白噪声是指零均值常方差的随机平稳序列；
③ 如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARMA等模型识别；
④ 对已识别好的模型，确定模型参数，最后应用预测并进行误差分析。

微分方程