图 - Java实现有向带权图的邻接表表示法

图 - Java实现有向带权图的邻接表表示法

1.邻接表

1.1 邻接表的介绍

上一篇文章我们已经介绍了图的定义，邻接矩阵的定义，以及通过Java实现无向带权图的邻接矩阵表示法，这一篇我将会展示通过Java实现有向带权图的邻接表表示法

• 用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间

• 对于无向图来说，如果 A[i][j]等于 1，那 A[j][i]也肯定等于 1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了

• 还有，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就三五百个而已。如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了

• 针对上面邻接矩阵比较浪费内存空间的问题，我们来看另外一种图的存储方法，邻接表（Adjacency List）

1.2 邻接表的存储形式

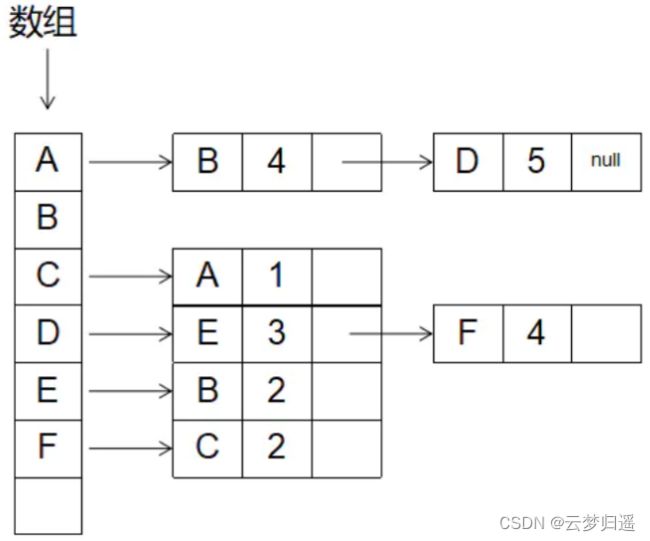
• 前面的数组存储的是所有的顶点，每一个顶点后面连接的块代表前面顶点所指向的顶点和路线的权值。如果该点还指向其他顶点，则继续在块后面添加。例如A指向了B权值是4，那么A后面就加上一块，之后发现A还指向D权值是5，那么就在块尾继续添加一块。其实也就是数组+链表的结构
  

2.Java实现有向带权图的邻接表表示法

package com.lagou;

import java.util.ArrayList;
import java.util.List;

/**
 * @author 云梦归遥
 * @date 2022/5/20 13:33
 * @description 有向带权图 - 邻接表法
 */
public class YesDirectionWeightTuMethod {
    public class TuNode{
        private String name; // 节点名称
        private int weight; // 边的权重
        private TuNode node; // 子节点

        public TuNode(String name){
            this.name = name; this.weight = 0; this.node = null;
        }
        public TuNode(String name, int weight){
            this.name = name; this.weight = weight; this.node = null;
        }
        public TuNode(String name, int weight, TuNode node){
            this.name = name; this.weight = weight; this.node = node;
        }
    }

    private List<Object> nodeList; // 节点的集合
    private TuNode[] adjacencyMatrix; // 邻接表中左侧所有节点

    public YesDirectionWeightTuMethod(int num){
        this.nodeList = new ArrayList<>(num);
        this.adjacencyMatrix = new TuNode[num];
    }

    // 插入节点
    public YesDirectionWeightTuMethod insert(String name){
        for (int i = 0; i < adjacencyMatrix.length; i++){
            if(adjacencyMatrix[i] == null){
                TuNode tuNode = new TuNode(name);
                adjacencyMatrix[i] = tuNode;
                nodeList.add(name);
                break;
            }
        }
        return this;
    }

    // 查询节点
    public String select(){
        TuNode tuNode = null;
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = 0; i < adjacencyMatrix.length; i++){
            if (adjacencyMatrix[i] != null){
                tuNode = adjacencyMatrix[i];
                stringBuilder.append("【" + tuNode.name + " (" + tuNode.weight + ")" + "】");
                TuNode temp = tuNode.node;
                while (temp != null){
                    if (temp.node != null){
                        stringBuilder.append("<" + temp.name + " (" + temp.weight + ")" + "> => ");
                    } else {
                        stringBuilder.append("<" + temp.name + " (" + temp.weight + ")" + ">");
                    }
                    temp = temp.node;
                }
                stringBuilder.append("\n");
            } else {
                break;
            }
        }
        return stringBuilder.toString();
    }

    // 添加边
    public YesDirectionWeightTuMethod addEdge(String firstNode, String secondNode, int weight){
        boolean firstNodeBoolean = nodeList.contains(firstNode);
        boolean secondNodeBoolean = nodeList.contains(secondNode);
        if (firstNodeBoolean && secondNodeBoolean){
            for (int i = 0; i < adjacencyMatrix.length; i++){
                if (adjacencyMatrix[i] != null && adjacencyMatrix[i].name.equals(firstNode)){
                    TuNode temp = adjacencyMatrix[i];
                    boolean exist = false;
                    while (temp.node != null){
                        if (temp.name.equals(secondNode)){
                            exist = true;
                            break;
                        }
                        temp = temp.node;
                    }
                    // 要进行建立边的节点之前没有建立过连接
                    if (!exist && !temp.name.equals(secondNode)){
                        TuNode tuNode = new TuNode(secondNode, weight);
                        temp.node = tuNode;
                        adjacencyMatrix[i].weight++;
                    }
                    break;
                }
            }
        }
        return this;
    }

    // 获取权重
    public int getWeight(String firstNode, String secondNode){
        boolean firstNodeBoolean = nodeList.contains(firstNode);
        boolean secondNodeBoolean = nodeList.contains(secondNode);
        int result = Integer.MAX_VALUE;
        if (firstNodeBoolean && secondNodeBoolean){
            for (int i = 0; i < adjacencyMatrix.length; i++){
                if (adjacencyMatrix[i] != null && adjacencyMatrix[i].name.equals(firstNode)){
                    TuNode temp = adjacencyMatrix[i];
                    boolean exist = false;
                    while (temp.node != null){
                        if (temp.name.equals(secondNode)){
                            exist = true;
                            break;
                        }
                        temp = temp.node;
                    }
                    // 要进行建立边的节点之前没有建立过连接
                    if (exist || temp.name.equals(secondNode)){
                        result = temp.weight;
                    }
                    break;
                }
            }
        }
        return result;
    }

    // 获取边
    public String getEdge(String firstNode){
        boolean firstNodeBoolean = nodeList.contains(firstNode);
        StringBuilder stringBuilder = new StringBuilder();
        if (firstNodeBoolean){
            for (int i = 0; i < adjacencyMatrix.length; i++){
                if (adjacencyMatrix[i] != null && adjacencyMatrix[i].name.equals(firstNode)){
                    TuNode temp = adjacencyMatrix[i];
                    stringBuilder.append("【" + temp.name + " (" + temp.weight + ")" + "】");
                    temp = temp.node;
                    boolean exist = false;
                    while (temp != null){
                        stringBuilder.append("<" + temp.name + " (" + temp.weight + ")> => ");
                        temp = temp.node;
                    }
                    break;
                }
            }
        }
        String string = stringBuilder.toString();
        string = string.substring(0, string.lastIndexOf(" => "));
        return string;
    }
}

进行测试

package com.lagou.test;

import com.lagou.YesDirectionWeightTuMethod;

/**
 * @author 云梦归遥
 * @date 2022/5/21 17:36
 * @description
 */
public class YesDirectionWeightTuMethodTest {
    public static void main(String[] args) {
        YesDirectionWeightTuMethod yesDirectionWeightTuMethod = new YesDirectionWeightTuMethod(5);
        yesDirectionWeightTuMethod.insert("A").insert("B").insert("C").insert("D").insert("E");
        yesDirectionWeightTuMethod
                .addEdge("A", "B", 1)
                .addEdge("A", "C", 2)
                .addEdge("A", "D", 3)
                .addEdge("A", "E", 4)
                .addEdge("B", "C", 5)
                .addEdge("B", "E", 6)
                .addEdge("C", "D", 7)
                .addEdge("D", "E", 8);
        String a = yesDirectionWeightTuMethod.getEdge("A");
        System.out.println(a);
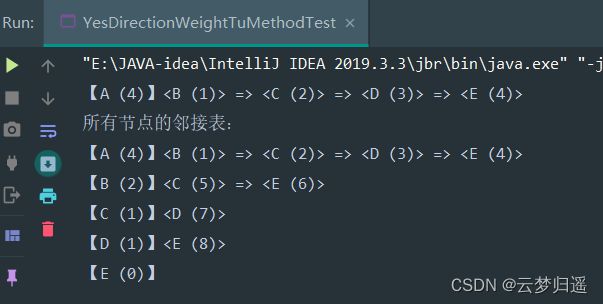
        String a1 = yesDirectionWeightTuMethod.select();
        System.out.println("所有节点的邻接表：\n" + a1);
    }
}

3.总结

• 邻接表的实现主要是通过一维数组 + 链表组成。
• 数组中存储着所有的节点
• 每个节点后面挂着一个链表，链表中的每个节点都是与节点有边的关系