pytorch——conv2d函数使用
卷积操作——理论实现
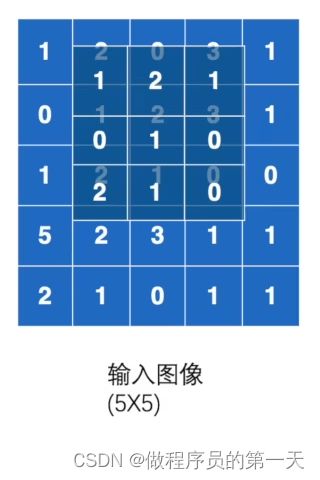
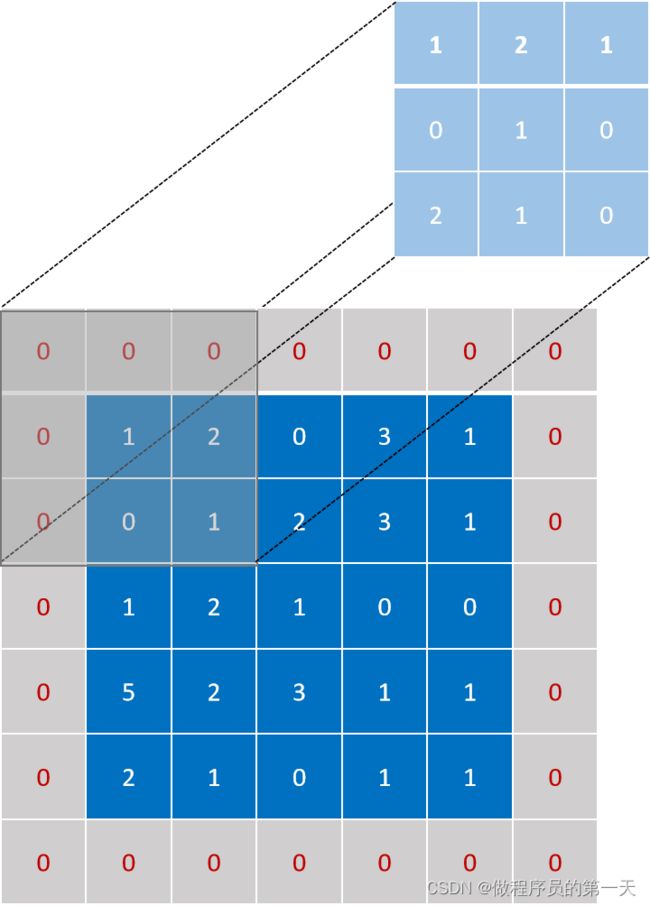
我们给出一道例题首先来说明卷积操作的流程,如下所示。下面给出了输入图像以及卷积核,输入图像的尺寸是5✖5的,而卷积核的尺寸是3✖3的。问:该图像经过如下卷积核操作后,其输出结果为多少?
执行流程如下:
首先,将卷积核与输入图像的前3×3大小的地方进行匹配,随后对应位置相乘并将 9 个相乘结果累加在一起,得到第一个输出的结果。
即有,1✖1+2✖2+0✖1+0✖0+1✖1+2✖0+1✖2+2✖1+1✖0=10
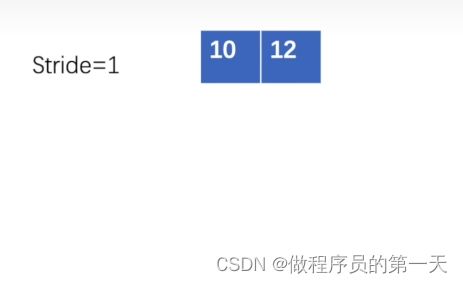
假使步长Stride = 1,则第二步匹配结果为:
即有,2✖1+0✖2+3✖1+1✖0+2✖1+3✖0+2✖2+1✖1+0✖0=12
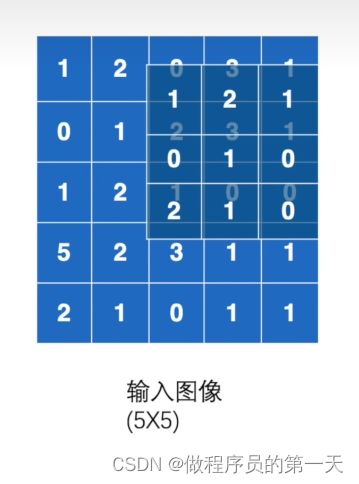
第三步匹配结果为:
即有,0✖1+3✖2+1✖1+2✖0+3✖1+1✖0+1✖2+0✖1+0✖0=12
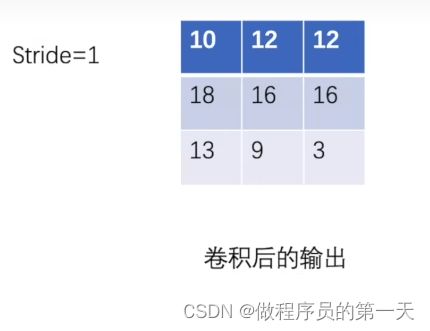
按照上述步骤,卷积核移动 9 次,最后得到结果为如下所示。
上图便是5✖5输入图像经过3×3卷积核卷积后的结果。
代码实现
首先来介绍一下conv2d函数,该函数主要作用为:在由多个输入平面组成的输入图像上应用2D卷积。
torch.nn.functional.conv2d(input, weight, bias=None,
stride=1, padding=0, dilation=1, groups=1,
padding_mode='zeros') → Tensorconv2d函数相关参数释义如下所示。
input:表示输入的图像张量,该张量包含四个维度,即:[ 输入图片数,输入图片的图层数(通道数),高,宽 ] 。
minibatch:batch中的样例个数
in_channels:每个样例数据的通道数
iH :每个样例的高(行数)
iW :每个样例的宽(列数)
weight:表示权重,也可以说成是卷积核。
out_channels:卷积核的个数
in_channels/groups:每个卷积核的通道数
kH :每个卷积核的高(行数)
kW :每个卷积核的宽(列数)
groups作用:对input中的每个样例数据,将通道分为groups等份,即每个样例数据被分成了groups个大小为 ( in_channel/groups, iH, iW ) 的子数据。对于这每个子数据来说,卷积核的大小为 ( in_channel/groups, kH, kW ) 。这一整个样例数据的计算结果为各个子数据的卷积结果拼接所得。
bias:偏置,tensor类型,大小是输出通道的大小。Default: None。
stride:表示卷积核每移动一次要跨越的长度,即卷积核的步长。
padding:输入图像周围的隐式填充。可以是单个数字或元组(padH、padW)。默认值:0,此时表示不填充。
其余参数不常用,后续遇到在解读。
给出程序进行验证:
import torch
import torch.nn.functional as F
# 输入图像信息
input = torch.tensor([[1, 2, 0, 3, 1],
[0, 1, 2, 3, 1],
[1, 2, 1, 0, 0],
[5, 2, 3, 1, 1],
[2, 1, 0, 1, 1]])
# 卷积核
kernel = torch.tensor([[1, 2, 1],
[0, 1, 0],
[2, 1, 0]])
input = torch.reshape(input, (1, 1, 5, 5)) # 输入数据:batch中只有一个样例数据,该样例数据有1个通道,高5,宽5。
kernel = torch.reshape(kernel, (1, 1, 3, 3)) # 卷积核:有1个卷积核,大小为:1个通道,高3,宽3。
output = F.conv2d(input, kernel, stride=1) # 卷积核步长为 1
print(output)
结果为:
tensor([[[[10, 12, 12],
[18, 16, 16],
[13, 9, 3]]]])这与我们前述理论部分得到的答案一致。
若将卷积核步长改为2,则结果又当如何?
output2 = F.conv2d(input, kernel, stride=2) # 卷积核步长为 2
print(output2)结果为:
tensor([[[[10, 12],
[13, 3]]]])padding参数理论概述及代码验证:
我们设置padding参数为1,则会在原输入图像周围拓展一行一列,且填充数据默认为0,如下图所示。
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
2 |
0 |
3 |
1 |
0 |
| 0 |
0 |
1 |
2 |
3 |
1 |
0 |
| 0 |
1 |
2 |
1 |
0 |
0 |
0 |
| 0 |
5 |
2 |
3 |
1 |
1 |
0 |
| 0 |
2 |
1 |
0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
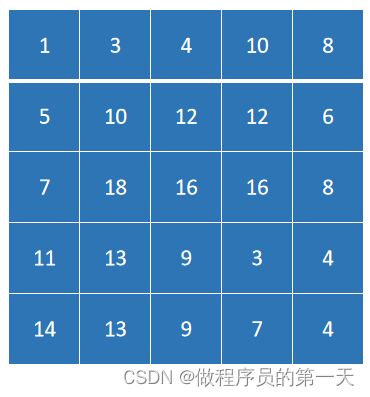
卷积核不变,按照前述规则,先匹配,再计算,最后得到结果。下图为第一次匹配结果。
卷积之后的结果为:
来看看代码运行结果。
output3 = F.conv2d(input, kernel, padding=1, stride=1)
# padding=1 :四周填充尺寸多一行一列,且填充数据默认为0
print(output3)结果为:
tensor([[[[ 1, 3, 4, 10, 8],
[ 5, 10, 12, 12, 6],
[ 7, 18, 16, 16, 8],
[11, 13, 9, 3, 4],
[14, 13, 9, 7, 4]]]])程序运行结果与理论计算得到的结果一致。
部分参考自:https://blog.csdn.net/jingOlivia/article/details/104728222