算法通关村第十六关:青铜挑战-滑动窗口其实很简单
青铜挑战-滑动窗口其实很简单
1. 滑动窗口基本思想
数组引入双指针的背景:
很多算法会大量移动数组中的元素,频繁移动元素会导致执行效率低下或者超时,使用两个变量能比较好的解决很多相关问题
数组双指针,之前介绍过 对撞型 和 快慢型 两种,滑动窗口思想就是快慢型的特例
滑动窗口
示例:
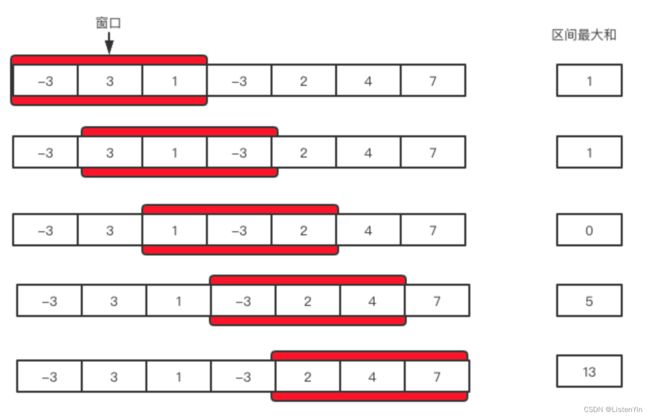
如下图所示,假设窗口是3,当不断有新数据来时,维护一个大小为3的一个区间,超过3就将新的放入,老的移走。
过程有点像火车在铁轨上跑。原始数据:铁轨,小区间:长度固定的火车。
有了区间,可以造题了,如找序列上连续3个数组的最大和是多少?
所谓窗口,就是建立两个索引left和right,保持 {left,right} 之间一共有3个元素,然后一边遍历序列,一边寻找,每改变一下就标记一下当前区间的最大和
掌握窗口和滑动的概念
窗口
- 两个变量left和right之间的元素,可以理解为一个区间
- 窗口可能固定,也可能变化
如果固定,需要先确定窗口是否越界
如果不固定,先判断是否满足要求,在执行逻辑处理
滑动
- 说明窗口是移动的,移动的是left和right两个变量,而不是序列中的元素
- left和right变量移动时,区间内元素发现变化
实际问题,窗口大小固定与不固定的两种场景
- 窗口大小固定:火车行驶
- 窗口大小不固定:两个老师带队学生外出,一个开路,一个断后,中间学生。两位老师之间的距离时大时小。
根据窗口大小固定与否,两种类型的题
- 固定:一般求哪个窗口的元素最大、最小、平均值、和最大、和最小等
- 不固定:一般求一个序列里最大、最小窗口是什么等
滑动窗口解题吃力的原因:
- 解题最终要落实到数组,特别是边界处理容易晕
- 有些元素的比较、判断比较麻烦,不仅要借助集合等工具,而且处理过程中还有一些技巧,不熟悉会导致解题难度大
- 堆!堆结构非常适合在流数据中找固定区间内的最大、最小等问题。因此滑动窗口经常和堆一起使用解决复杂的问题
滑动窗口和双指针的区别
- 滑动窗口是双指针的一种类型;
- 滑动窗口主要关注两个指针之间元素的情况,应用范围更小一些;
- 双指针的应用范围更大,花样也更多。
2. 两个入门题
2.1 子数组最大平均数
LeetCode 643
https://leetcode.cn/problems/maximum-average-subarray-i/
思路分析
典型的滑动窗口,窗口大小固定了,就是K
先读取K个,然后逐步让窗口向前走就可以了
代码实现
class Solution:
def findMaxAverage(self, nums: List[int], k: int) -> float:
window_sum = 0
# 第一步:求第一个窗口的和
for i in range(k):
window_sum += nums[i]
# 第二步:遍历,每次右边增加一个,左边减去一个,重新计算窗口的最大值
res = window_sum
left = 0
for right in range(k, len(nums)):
window_sum = window_sum + nums[right] - nums[left]
res = max(res, window_sum)
left += 1
return res/k
2.2 最长连续递增序列
LeetCode674
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/
思路分析
方法1:滑动窗口
这是一个窗口大小变化的题目
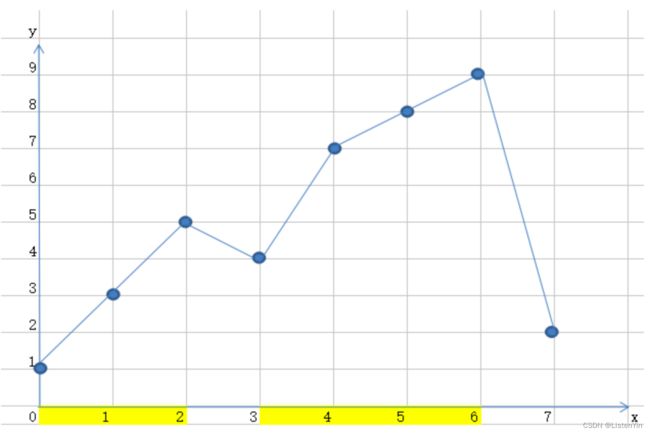
如图所示,实例序列 1,3,5,4,7,8,9,2 最长递增子序列 4,7,8,9 结果应返回4
我们可以从第2个元素开始,定义 [left, right] 区间来表示当前的递增区间,执行如下操作
- 当前遍历的元素比它左边的元素大,right增加
- 否则就将left跳到right的起始位置,重新开始计算
方法2:
一边遍历,一边统计每个递增区间的长度,如果长度超过之前左右区间的长度,将其保留
代码实现
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
# 方法1:滑动窗口
res = 1
left = 0
for right in range(1, len(nums)):
if nums[right] <= nums[right - 1]:
left = right
res = max(right - left + 1, res)
return res
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
# 方法2
cur_len = 1
res = 1
for i in range(1, len(nums)):
if nums[i] > nums[i-1]:
cur_len += 1
else:
cur_len = 1
res = max(res, cur_len)
return res