第66步 时间序列建模实战:ARIMA建模(SPSS)
基于WIN10的64位系统演示
一、写在前面
从这一期,我们使用SPSS进行SARIMA模型的构建。
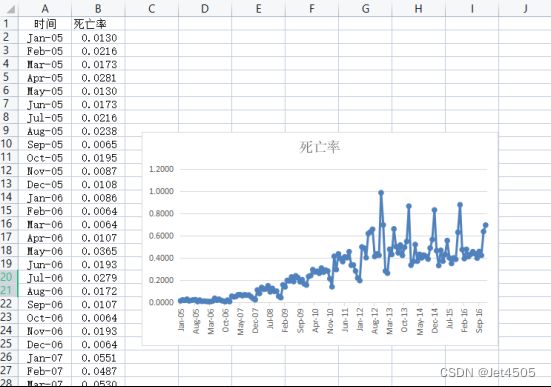
同样,使用某省2005年1月至2016年12月AIDS死亡率的时间序列数据。
二、SPSS建立SARIMA实战
(1)录入数据和格式调整
双击打开IBM SPSS Statistics 27软件,把数据复制进SPSS界面:
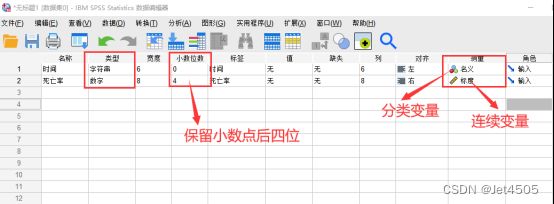
数据格式调整:打开“变量视图”,按需调整,如“小数位数”、“数据类型”、“测量”等。
(2)时间序列数据转变
我们需要把“时间”这一列,转变成SPSS软件能识别的时间序列信息。
打开“定义日期和时间”面板,定义“年”和“月”还有“周期”:
点击确认后,可以看到。软件自动生成了“YEAR”、“MONTH”和“DATE”三列,说明时间序列转换完毕。
(3)自相关和偏相关图
虽然说只是看看而已,但是文章中还是得放的,所以还是得展示。
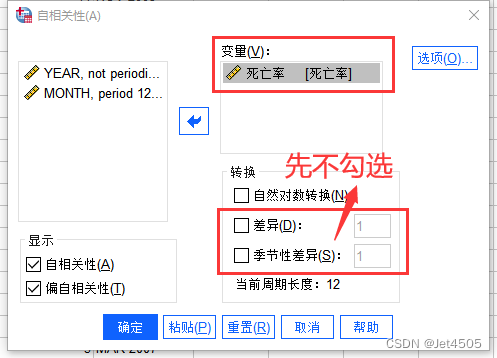
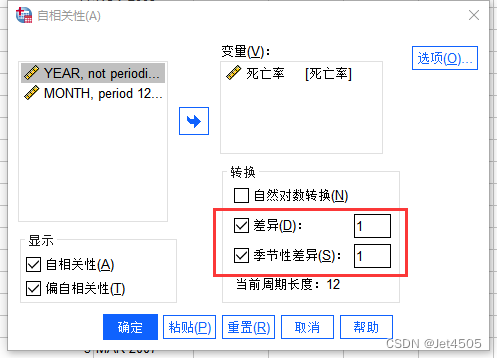
打开“自相关”对话框,先看不拆分的:
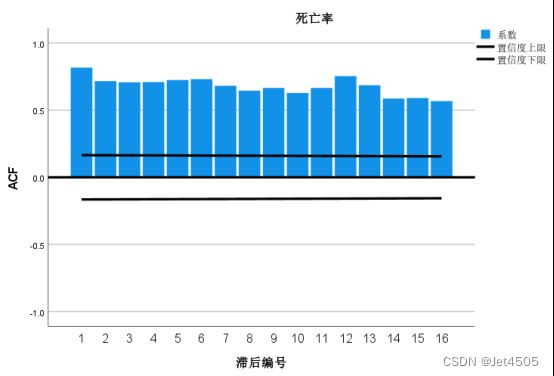
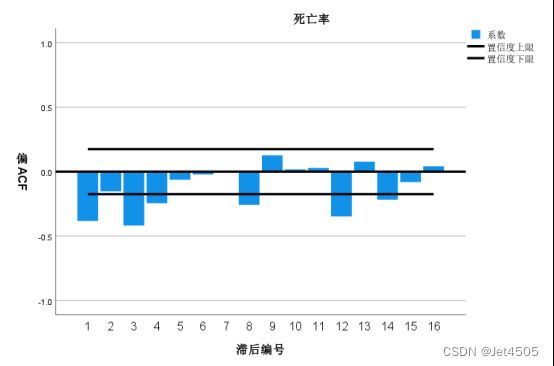
由图可知,在自相关图和偏相关图中,在12、24对应的柱子均处于高水平,由此可判断该序列具有季节性(周期为12个月)。另外,从自相关图中可以看到,均超过虚线,因此该序列为不平稳序列,应该进行拆分运算。
进行了拆分运算,分为一般拆分和季节拆分,进行一次一般拆分,则d = 1,进行一次季节拆分,则D = 1。看着图,就先这样吧。
(4)ARIMA建模
策略还是一样的:采用逐个参数尝试的方法,根据一般经验来看,疾病发病率ARIMA模型的p、q、P和Q选取的范围为0、1和2即可,因此需要尝试81(3×3×3×3=81)个ARIMA模型,再根据AIC和SBC准则以及参数是否通过假设检验来选出最佳的模型。
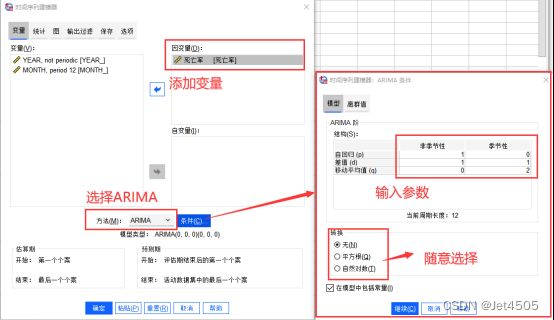
展示软件如何操作,这里以构建ARIMA(1,1,0)(0,1,2)12模型为例子:
结果解析:
由于有一个参数没差异,因此不考虑此模型,也可以填入下表,不然容易混乱。
继续下一个,ARIMA(1,1,1)(0,1,1)12模型:
按照这个流程,把81个模型全部撸一遍,找出最终的模型。
(5)最优ARIMA建模拟合和预测
假设ARIMA(1,1,1)(0,1,1)12是最优模型(我盲猜的,不过大概率是),如何得出拟合值和预测值呢?
先看拟合值,只需要在构建模型的时候勾选“保存”的选项,即可:
打开数据面板,可以发现多出了四列数据,复制到作图软件作图即可:
再看预测值,比如说我们要预测2017年1月到2017年12月的数据。先在数据面板填好这三列:
(6)评估模型的拟合和预测性能
计算mean square error (MSE)(均方差), mean absolute error (MAE)(平均绝对误差) 和mean absolute percentage error (MAPE)(平均相对误差)公式如下:
其中,Xt为实际值,Xt^为预测值,n为总数。
计算以上误差可以在excel中实现,最后的结果如下:
| 拟合误差 |
预测误差 |
|||||
| MAE |
MAPE |
MSE |
MAE |
MAPE |
MSE |
|
| ARIMA |
自己算 |
自己算 |
自己算 |
算不出 |
算不出 |
算不出 |
我们没有对已知数据进行拆分,所以只能算出拟合误差。
一般来说,2005年1月至2016年12月的数据,会用2005年1月至2015年12月的数据建模,去预测2016年1月至2016年12月的数据,这样就会得到拟合误差和预测误差了。
一般认为,MAPE小于0.1则预测效果优秀。
三、写在后面
(1)SPSS不能算单位根检验,而且SPSS的算法跟Eviews也有些区别,所以不同模型在同一个数据的建模,结果是不一样的。甚至不同版本都是这个情况,所以在写文章的时候,要注明软件和版本号!!!
(2)关于杨-博克斯Q(18)统计检验:它对模型中残差误差的随机检验,当其显著性小于0.05时说明残差误差不是随机的。在我们的例子中,它是小于0.05的,说明原始数据中有些信息还没提取出来。可以考虑进一步优化模型,比如调整拆分、自然对数处理等,实在不行,说明ARIMA处理不完全这个数据,那得用组合模型来处理了。毕竟ARIMA模型只能提取数据的线性信息。
四、数据
链接:https://pan.baidu.com/s/1WKNmpFA4ySE09tTSN8uvrw?pwd=wfyt
提取码:wfyt