目标识别基础知识总结
目标识别基础知识
文章目录
- 目标识别基础知识
-
-
- 一、IOU定义
- 二、非极大值抑制
-
- 非极大值抑制流程:
- 三、有监督预训练与无监督预训练
- 四、超参数
- 五、[均值平均精度Map(Mean Average Precision)](https://www.cnblogs.com/zongfa/p/9783972.html)
- 六、[感受野(Receptive field)](https://iphysresearch.github.io/posts/receptive_field.html)
-
- 感受野的计算方式:
- 七、[随机梯度下降(SGD)](https://blog.csdn.net/zb123455445/article/details/78832557)
- 八、图像金字塔
-
一、IOU定义
物体检测需要定位出物体的bounding box,就像下图中,我们不仅要定位出bounding box,还要是被出bounding box中的物体就是车辆。对于bounding box的定位精度有一个很重要的概念,因为我们的算法不可能百分百与人工标注的数据完全匹配,因此就存在一个定位精度的评价公式:IOU
![]()
IOU即为两个bounding box的重叠程度,如下图所示:
![]()
矩形框A,B的重合度IOU的计算公式为:
I O U = ( A ∩ B ) / ( A ∪ B ) \mathrm{IOU}=(\mathrm{A} \cap \mathrm{B}) /(\mathrm{A} \cup \mathrm{B}) IOU=(A∩B)/(A∪B)
即A,B重叠面积:
I O U = S I / ( S A + S B − S I ) \mathrm{IOU}=S I /(S A+S B-S I) IOU=SI/(SA+SB−SI)
二、非极大值抑制
(参考自:https://www.jianshu.com/p/d452b5615850)
以目标检测为例:目标检测的过程中在同一目标的位置上会产生大量的候选框,这些候选框相互之间可能会有重叠,此时我们需要利用非极大值抑制找到最佳的目标边界框,消除冗余的边界框。
![]()
如上左图为不采用非极大值抑制,则图中中有多个候选框结果,每个边界框都有一个置信度(confidence score)。而右图为采用非极大值抑制后的结果,更符合我们在检测中的要求。
非极大值抑制流程:
- 将候选框根据置信度得分进行排序;
- 选择置信度最高的候选框添加到最终的输出列表中,将其从候选框列表中删除;
- 计算置信度最高的边界框与其他候选框的IOU;
- 删除IOU大于阈值,且置信度小于最高置信度的候选框;
- 重复上述过程。
例如:
- 阈值为0.6
- 阈值为0.5
- 阈值为0.4
三、有监督预训练与无监督预训练
1.有监督预训练
又称为迁移学习,即将训练好的参数拿到另一个任务中作为神经网络初始值,相比于采用随机初始化的方法可以提升很高的精度。
2.无监督预训练
预训练阶段不需要人工标注数据,就叫做无监督预训练。
四、超参数
超参数是开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,给学习机选择一组最优超参数,以提高学习的性能和效果。模型参数是根据数据自动估算的。但模型超参数是手动设置的,并且在过程中用于帮助估计模型参数。
超参数也是一种参数,它具有参数的特性,比如未知,也就是它不是一个已知常量。一种手工可配置的设置,需要为它根据已有或现有的经验指定“正确”的值,也就是人为为它设定一个值,它不是通过系统学习得到的。
五、均值平均精度Map(Mean Average Precision)
通过IOU值与设定的IOU阈值进行比较,可以计算出每个图像的正确检测次数(A),且对于每个图像,我们都知道其真实目标信息,也就是知道了该图像中给定类别的实际目标(B)的数量。即可以用下式来衡量该模型的精度。
Precesion C = N ( TruePositives ) C N ( TotalObjects ) C \text {Precesion}_{C}=\frac{N(\text {True} \text {Positives})_{C}}{N(\text {TotalObjects})_{C}} PrecesionC=N(TotalObjects)CN(TruePositives)C
即,给定图像的C类Precision等于图像正确预测(True Positives)的数量除以在图像这一类的总的目标数量。
将一定图片数量的精度值求和,除以图片数量即该类的平均精度值。如下式:
AveragePrecision C = ∑ Precision C N ( Totallmages ) C \text {AveragePrecision}_{C}=\frac{\sum \text {Precision}_{C}}{N(\text {Totallmages})_{C}} AveragePrecisionC=N(Totallmages)C∑PrecisionC
即一个C类的平均精度等于在验证集上所有的图像对于类C的精度值的和除以有C类这个目标的所有图像的数量。
将每一类的平均精度值求和,除以类的数量,即MAP(均值平均精度)。如下式:
Mean Average Precision = ∑ AveragePrecision C N ( Classes ) \text {Mean Average Precision}=\frac{\sum \text {AveragePrecision}_{C}}{N(\text {Classes})} Mean Average Precision=N(Classes)∑AveragePrecisionC
在使用MAP时,需要满足以下条件:
- MAP总是在固定的数据集上计算。
- 它不是量化模型输出的绝对度量,但是是一个比较好的相对度量。当我们在流行的公共数据集上计算这个度量时,这个度量可以很容易的用来比较不同目标检测方法。
- 根据训练中类的分布情况,平均精度值可能会因为某些类别(具有良好的训练数据)非常高(对于具有较少或较差数据的类别)而言非常低。所以我们需要MAP可能是适中的,但是模型可能对于某些类非常好,对于某些类非常不好。因此建议在分析模型结果的同时查看个各类的平均精度,这些值也可以作为我们是不是需要添加更多训练样本的一个依据。
六、感受野(Receptive field)
八股式定义:在卷积神经网络CNN中,决定某一层输出结果中一个元素所对应的输入层的区域大小,被称作感受野receptive field。
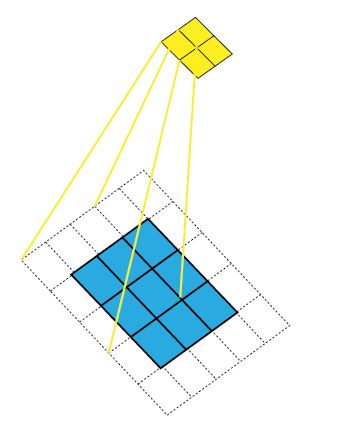
通俗解释为:feature map上的一个点对应输入图上的区域。
对5x5的绿色特征图采用卷积核(kernel size)大小k=3x3,填充(padding size)大小p=1x1,步长(stride)s=2x2,进行卷积生成蓝色特征图,如上图。
对生成的3x3蓝色特征图采用相同卷积操作生成黄色特征图,如上图。
此时我们生成了2x2的黄色部分特征图,但是只看特征图,我们无法得知特征的位置(感受野的中心位置)和区域大小(感受野的大小),
感受野的计算方式:
这里提供感受野的计算器:Fomoro AI
某一层特征上的感受野大小依赖的要素有:每一层的卷积核大小 k,填充大小 p,步长 s。在推导某层的感受野时,还需要考虑到该层之前各层上特征的的感受野大小 r,以及各层相邻特征之间的距离 j(jump)。
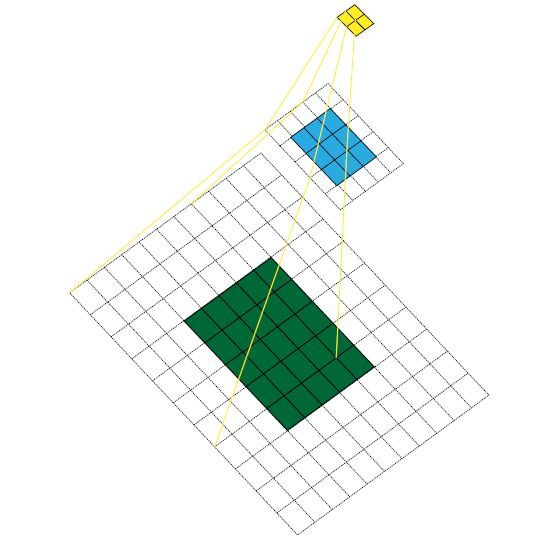
![]()
上图中5x5的蓝色特征图采用卷积核(kernel size)大小k=3x3,填充(padding size)大小p=1x1,步长(stride)s=2x2,进行卷积生成3x3绿色部分特征图,对生成的3x3绿色特征图采用相同卷积操作生成2x2黄色特征图。
- Layer 0:绿色特征图对应的感受野由阴影部分来表示,即绿色特征块对应的感受野大小为3x3,
start1表示几何半径为0.5(对应于阴影面积覆盖到的绿色面积的几何半径)。 - Layer 1:黄色特征图对应的感受野由阴影部分表示,特征野大小为7x7,start2表示几何半径为0.5。
对于某一卷积层(卷积核(kernel size)大小 k,填充(padding size)大小 p,步长(stride) s)上某一特征的感受野大小公式为:
j out = j i n ∗ s j_{\text { out }}=j_{i n} * s j out =jin∗s
该公式计算相邻特征之间的距离(jump)。各层中的特征之间的距离依赖于 stride ,并且逐层累积。(注意:输入图像的作为起始像素特征,它的特征距离(jump) 为1。)
r out = r i n + ( k − 1 ) ∗ j i n r_{\text { out }}=r_{i n}+(k-1) * j_{i n} r out =rin+(k−1)∗jin
该公式计算某层的特征的感受野大小。它依赖于上一层的特征的感受野大小rin和特征之间的距离jin,以及该层的卷积核大小 k。输入图的每个像素作为特征的感受野就是其自身,为1。
s t a r t o u t = s t a r t i n + ( k − 1 2 − p ) ∗ j i n s t a r t_{\mathrm{out}}=s t a r t_{\mathrm{in}}+\left(\frac{k-1}{2}-p\right) * j_{\mathrm{in}} startout=startin+(2k−1−p)∗jin
该公式计算特征感受野的几何半径。对于处于特征图边缘处的特征来说,这类特征的感受野并不会完整的对应到原输入图像上的区域,都会小一些。初始特征的感受野几何半径为 0.5。
七、随机梯度下降(SGD)
八、图像金字塔
图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低的图像集合。金字塔的底部是待处理图像的高分辨率表示,而顶部是低分辨率的近似。当向金字塔的上层移动时,尺寸和分辨率就降低。