ABtest笔记
一. 统计学原理(知识预备)
1. 三大抽样分布、第一/二类错误
- 卡方分布
参考资料:卡方分布_LittleDorcas博客-CSDN博客_卡方分布、《概率论与数理统计》
定义:
设是来自标准正态分布的样本,则称统计量
服从自由度为n的卡方分布,记为,其概率密度曲线pdf:
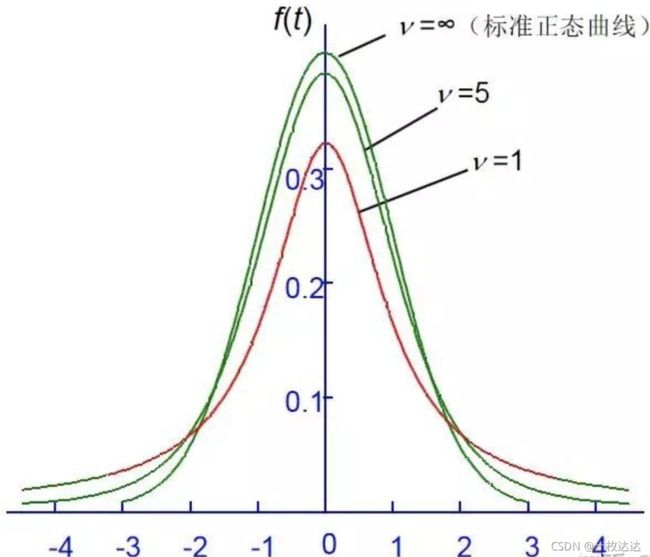
当自由度n逐渐增大,曲线逐渐接近正态分布。
- t分布
参考资料:统计学-t分布 - 知乎、《概率论与数理统计》
定义:
设,且X, Y相互独立,则称随机变量
服从自由度为n的t分布,记为,其概率密度曲线pdf:
当自由度n逐渐增大,曲线逐渐接近标准正态分布。
- F分布
参考资料:《概率论与数理统计》
定义:
设,且U, V相互独立,则称随机变量
服从自由度为的F分布,记为,概率密度曲线pdf:
- 一二类错误
参考资料:《概率论与数理统计》
一二类错误的定义是基于假设为![]() 的情况;
的情况;
第一类错误是指“实际上![]() 成立,但我们犯错认为应该拒绝
成立,但我们犯错认为应该拒绝![]() ”,也就是我们常遇到的显著性水平
”,也就是我们常遇到的显著性水平![]() 。
。
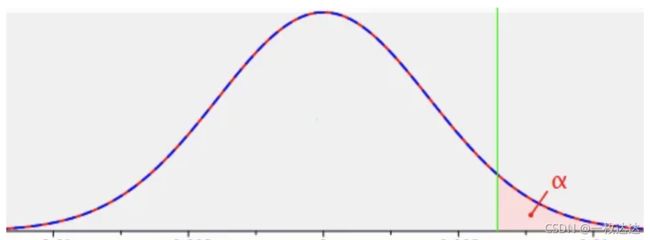
举例,如果华人的身高服从正态分布,当![]() 设置为0.05,绿线对应身高为1米9,此时抽样刚好抽到了姚明,他的身高超过了显著性水平对应的身高临界值,从而你判断成“姚明不是华人”,那么你就犯了第一类错误。
设置为0.05,绿线对应身高为1米9,此时抽样刚好抽到了姚明,他的身高超过了显著性水平对应的身高临界值,从而你判断成“姚明不是华人”,那么你就犯了第一类错误。
第二类错误是指“实际上![]() 不成立,但我们犯错认为应该接受
不成立,但我们犯错认为应该接受![]() ”,这在abtest中常用到,表示为
”,这在abtest中常用到,表示为![]() (power)。需要注意的是,power通常要搭配显著性水平alpha看才有意义。
(power)。需要注意的是,power通常要搭配显著性水平alpha看才有意义。
举例,你想研究欧美人是否平均体重比亚洲人高,假设实际上亚洲人(红曲线)、欧美人(蓝虚线)的体重均服从正态分布,方差相同,但欧美人体重均值稍高点。![]() 假如设置为40%,绿线对应的体重是75kg,那在这里的意思是假如你抽样得到的体重低于75kg的欧美人占比超过40%,你就相信欧美人并没有明显高于亚洲人,反之则相信欧美人明显较高。
假如设置为40%,绿线对应的体重是75kg,那在这里的意思是假如你抽样得到的体重低于75kg的欧美人占比超过40%,你就相信欧美人并没有明显高于亚洲人,反之则相信欧美人明显较高。
注意,这里你只知道亚洲人的体重分布,并不知道欧美人的体重分布。
你此时抽了10个欧美人做样本,发现有5个人体重低于75kg,5个人大于75kg,基于你的样本计算出的,你就接受了![]() 猜想,认为欧美人没有明显高于亚洲人,那么你就犯了第二类错误。
猜想,认为欧美人没有明显高于亚洲人,那么你就犯了第二类错误。
特别说明,这种第二类错误在产品改版的商业场景里往往是不能容忍的。假如红曲线是上一代产品每个用户使用时长的分布,蓝曲线是你准备全量上线的产品的表现,那么你造成的错误是“产品的使用体验收到影响,但你认为没有影响”,这是很恐怖的。
2. 最小样本量测算
参考文献:《Fundamentals of Biostatistics》,链接:Fundamentals of Biostatistics
第228页,7.6 Sample-size Determination
- 首先,为什么需要计算最小样本量?
如果你顺着看下来,在上面体重的例子中你就看到了,为什么我们会犯第二类错误?因为你只抽样了10个样本,太少了,缺乏科学性,你有很大可能会得到错误的结论,这肯定是不能接受的。因此我们需要一个能支持我们信服结论的最小样本量。
- 基于t分布近似正态分布的最小样本量推算
假设X服从正态分布![]() ,那么统计量
,那么统计量
会服从的t分布,其中![]() 是样本的均值,样本方差
是样本的均值,样本方差![]() 是
是![]() 的无偏估计。
的无偏估计。
证明过程:
当n足够大时,t分布近似为标准正态分布,因此得到
![]() 或
或 ![]()
 图参考自《Fundamentals of Biostatistics》,需要注意的是,这幅图的虚线是原分布即上一代产品,实线才是你要研究的下一代产品。
图参考自《Fundamentals of Biostatistics》,需要注意的是,这幅图的虚线是原分布即上一代产品,实线才是你要研究的下一代产品。
推导过程:
先根据原分布的显著性水平,算出接受域和拒绝域的界值为![]()
再基于下一代产品的分布曲线,算出此时浅灰色+深灰色部分的总面积为![]()
那有![]()
算吧,最后你可以得到最小样本量:![]()
第一大节讲的是abtest实验的理论基础,即怎么科学判断产品的迭代是否真的有影响,通常X会选择一些你关心的实验指标,比如一些商业化指标、用户体验指标。
二. 分层分流策略
随机化、为什么对全局的推算不会被稀释
可参考的资料:一文搞懂AB Testing的分层分流 | 人人都是产品经理
- 通常实验背景
对于APP和WEB的实验来说,ab实验的各个分组都是同时进行的,也就是我日均有100万个用户,我是对这100万个用户实时不同的策略/分组,来产生同步的对比;而不是我100万个用户,直接全量上线新版本,然后对前后版本的用户表现进行异步对比。
通常的分组方式有AB、AAB,A是对照组,B是实验组。AB类型的分组需要设置空跑期,即实验组B先保持和A一样的原策略不变,看实验指标是否发生显著性变化,如果是,则说明分组的随机化不够理想;AAB类型的分组,则可以通过两组对照组A1/A2的对比,来估计分组的随机化是否得到保证。AAB节省空跑期的时间,但其实AA随机化效果理想依然很难说服别人AB组的随机化也是理想的,这个时间成本和实验严谨性的balance要视业务情况而定。
- 分层分流机制
实验分组带来了第一个问题:流量不够用!
平常一个实验每个组可能占用5%的流量,即100万占用5万,简单的AAB就已经占用15%,更别说有些实验需求是AABCD多个实验组;但一个APP内可能会同时有数十个实验的需求,显然流量是不够的。
因此,引进了分层分流机制,以充分利用流量。
对于分层分流机制的基本介绍,上面的参考资料中有较详细的阐述,这里我做补充和举例。
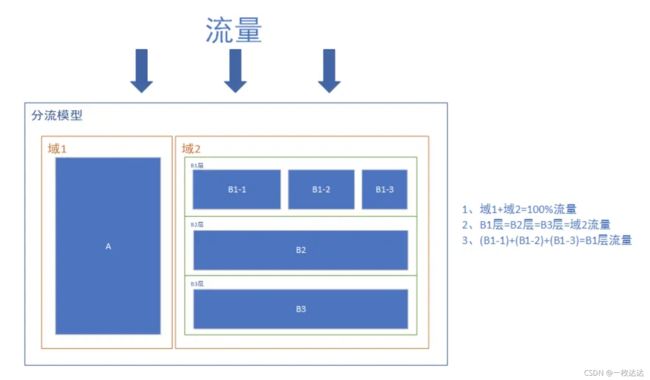
对应上图,拿支付宝举个例子(请打开支付宝享用下文),注意流量的流向是向下的。
域1是开了支付宝黑金会员的用户,马老师希望域2中对非黑金会员的用户实施的任何策略/改版,都不要影响到黑金会员这边的流量,因此单独划开;又或者,也可以划分出域3,这部分流量不使用任何策略,当作所有实验的一个对照的基准,也就是“让我看看你捣鼓半天到底跟原封不动有啥分别”。他们是互斥的流量。
B1:UI设计层
B2:决定给你推荐哪种广告的广告层
B3:决定给你推荐哪种内容的内容层
B1-1:UI设计层-安卓域
B1-2:UI设计层-苹果域
B1-3:UI设计层-其他终端域
这里,B1-1、B1-2、B1-3也是域,是互斥的流量,因此层和域之间可以互相嵌套。
你现在针对苹果端的UI界面想做一些改版,比如把“我的”里面的logo放大10%的实验。也许此时B2广告层打算把推荐算法的超参数进行一些调整,你的实验和他们的实验互不干扰,因为层之间的流量经过了正交,分层分流机制会把B1-1/B1-2/B1-3的流量整合并重新打散,再进入B2层。
如此,假如域1占了10%的总流量,那可能你在B1-2的实验用了30%总流量,B2层的广告算法实验用了90%总流量,就实现了流量的充分利用。
- 分流与实验分组的时机、推全逻辑
举例说明
实验:对非会员用户的“我的”界面进行改版,不分终端类型(安卓、苹果等)
经测算最小样本量:3000个
总流量:100万
假定非会员用户中,会打开“我的”界面的用户占a%
分流与分组逻辑:
1) 先在非会员域(域2),UI层进行实验,抽两组5%流量(5万);
2) 后在这两组5%流量的用户,当用户的终端显示出“我的”界面时,被分到对应的对照/实验组中,如此产生了真正意义的对照组、实验组。注意需要保证样本数大于最小样本量。
产生两个疑问:
1) 为什么要先抽流量再分流,而不是直接分流(当有B1-UI层的用户终端显示出“我的”界面时直接随机加入对照组A或者实验组B)?
答:我认为这样做,一方面是保证实验所在的层或域中的其他流量同质,先抽流量再分流,则B1层中其他用户打开“我的”界面的比例还是a%,即其他流量与B1层在经过分组前的整体流量的特征都是相同的;另一方面有利于实验结束时对于实验效果进行推全计算,即你需要保证5%*a%的最终样本量大于最小样本量,在你得到实验组B的总体用户使用APP时长比实验组A多了10,000分钟的同时,你可以直接除以5%,得到实验B策略推全后可以让整个APP的用户使用时长多200,000分钟,但如果你是直接分流,则你需要知道a%的具体数值,才能得到推全的结果。
2) 分流时机为什么突出是显示“我的”界面时,而不是打开“我的”界面时?有什么不同吗?
答:分流时机不准常会带来样本量不够、流量不均的问题。你需要保证你分流的时机,正好是用户是否被策略影响到的时机。
我们通常说打开,指的是一个触发时机,即你点击了支付宝右下角的“我的”按钮,但这跟“我的”界面显示在手机上,是前后的两个事件,他们相隔的时间可能很短所以平时你没有感知到。
倘若,假如,你点击“我的”按钮后,“我的”界面需要相隔十秒钟再显示出来,而相当部分用户因为不厌其烦退出了支付宝,那当你将点击“我的”按钮作为分流策略的触发时机时,实际上被新的页面策略影响到的用户要明显小于这部分被安排进对照组/实验组的用户;甚至,因为现实中并没有完完全全的随机化,这两组5%流量中显示“我的”界面的用户并不一定都是相等的a%,因此会造成最终实际上被策略影响到的对照组A和实验组B的用户数有相当的gap。
鸣谢
文章最后,鸣谢alan家乐老师对本文的大力指导和支持!