如何利用贝叶斯模型做广告投放策略优化?
1. 背景介绍
假设你是一家电子商务公司的市场营销团队成员,负责广告投放的策略优化。你希望利用历史广告投放数据来构建一个模型,以了解不同因素如广告预算(Budget)和广告类型(AdType)对投放效果(Effect)的影响,并预测未来的广告投放效果(Conversion)。
2. 实现方法
2.1 概率图
Budget能取两个值,概率如下:
| Budget_0 | Budget_1 |
|---|---|
| 0.7 | 0.3 |
AdType能取两个值,概率如下:
| AdType_0 | AdType_1 |
|---|---|
| 0.8 | 0.2 |
Conversion能取两个值,与Budget和AdType的概率如下:
| Budget | Budget_0 | Budget_0 | Budget_1 | Budget_1 |
|---|---|---|---|---|
| AdType | AdType_0 | AdType_1 | AdType_0 | AdType_1 |
| Effect_0 | 0.9 | 0.7 | 0.7 | 0.4 |
| Effect_1 | 0.1 | 0.3 | 0.3 | 0.6 |
Conversion能取两个值,与Effect的概率如下:
| Effect | Effct_0 | Effect_1 |
|---|---|---|
| Conversion_0 | 0.85 | 0.6 |
| Conversion_1 | 0.15 | 0.4 |
2.2 业务流程
对2.1中的信息进行梳理,简单画出对应的业务逻辑图,如下所示:
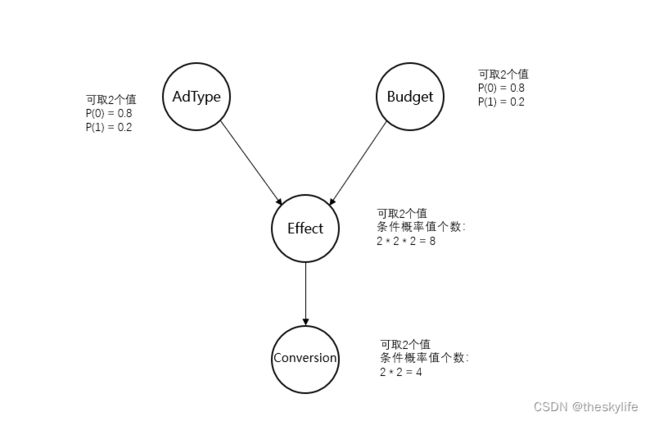
2.3 实现代码
基于2.1和2.2中的信息,为求Budget为0,AdType为1时,对Conversion的影响,以及其概率。实现代码如下:
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
# 创建一个贝叶斯网络
# budge为广告预算,adType为广告类型 Effect为投放效果,Conversion为转化率
# 可以参考2.2中的图像
model = BayesianNetwork([('Budget', 'Effect'), ('AdType', 'Effect'),
('Effect', 'Conversion')])
# 定义节点的条件概率分布(CPD)
cpd_budget = TabularCPD(variable='Budget',
variable_card=2,
values=[[0.7], [0.3]])
cpd_adtype = TabularCPD(variable='AdType',
variable_card=2,
values=[[0.8], [0.2]])
cpd_effect = TabularCPD(variable='Effect',
variable_card=2,
values=[[0.9, 0.7, 0.7, 0.4], [0.1, 0.3, 0.3, 0.6]],
evidence=['Budget', 'AdType'],
evidence_card=[2, 2])
cpd_conversion = TabularCPD(variable='Conversion',
variable_card=2,
values=[[0.85, 0.6], [0.15, 0.4]],
evidence=['Effect'],
evidence_card=[2])
# 将CPD添加到模型中
model.add_cpds(cpd_budget, cpd_adtype, cpd_effect, cpd_conversion)
# 验证模型的结构和CPD是否一致
assert model.check_model()
# 创建VariableElimination对象,用于推理
inference = VariableElimination(model)
# 进行变量推理
result = inference.query(variables=['Conversion'],
evidence={
'Budget': 0,
'AdType': 1
})
- 先利用已知信息,求得Effect为0的概率为0.7,为1的概率为0.3
- 再利用上面的Effect概率,求出对应的Conversion概率。
- Conversion为0:0.7 * 0.85 + 0.3 * 0.6 = 0.775
- Conversion为1: 0.7 * 0.15 + 0.3 * 0.4 = 0.225
3.后记
贝叶斯分析,一般需要的数据比较多,计算起来会较为复杂,适合处理一些简单的问题,但是对于复杂的问题,在处理时会比较麻烦;另外贝叶斯分析需要使用到一些主观概率,如果这些概率有问题,难免会影响对应的结果。虽说贝叶斯有以上缺点,但是能对结果的可能性进行数量化评价。
因此,在使用贝叶斯分析时,要注意考虑问题的场景。
