MATLAB实现数据插值

目录

一.理论知识

二.一维插值实例

三.二维插值实例

---

一.理论知识

所谓插值，顾名思义，插入数值。很多时候，我们仅有离散点上的数据，这时如果我们想要分析变量之间的函数关系，则无法实现。但如果通过插值处理，当精度足够高时，离散点便可以变成连续的曲线~这就是插值的实用意义。

如下是插值法的原理，大家看一下就好了

常见的插值法有4种：拉格朗日插值、分段线性插值、埃尔米特(Hermite)插值 、三次样条插值

二.一维插值实例

 

p = interp1 (x, y, new_x, 'spline');

如上的代码即可实现一维插值，不同插值方式只需要修改第4个参数即可。

已知人口数：

年份	人口(万）
2009	133126
2010	133770
2011	134413
2012	135069
2013	135738
2014	136427
2015	137122
2016	137866
2017	138639
2018	139538

 

x=2009:1:2018;
y=[133126
133770
134413
135069
135738
136427
137122
137866
138639
139538
];
new_x=2009:0.1:2018;
p = interp1 (x, y, new_x, 'spline');
plot(new_x,p)

三.二维插值实例 

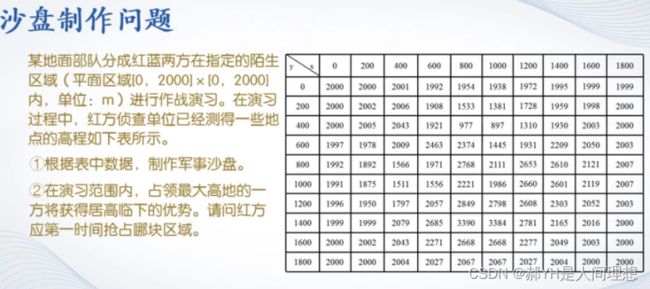
首先分享一个沙盘制作问题：

实现代码：

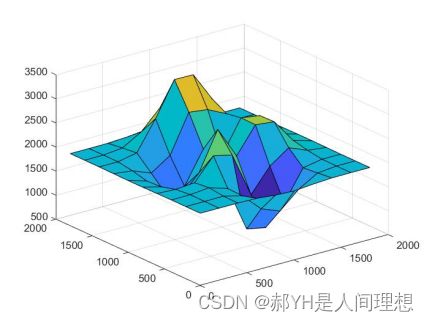
z=[2000,2000,2001,1992,1954,1938,1972,1995,1999,1999;2000,2002,2006,1908,1533,1381,1728,1959,1998,2000;2000,2005,2043,1921,977,897,1310,1930,2003,2000;1997,1978,2009,2463,2374,1445,1931,2209,2050,2003;1992,1892,1566,1971,2768,2111,2653,2610,2121,2007;1991,1875,1511,1556,2221,1986,2660,2601,2119,2007;1996,1950,1797,2057,2849,2798,2608,2303,2052,2003;1999,1999,2079,2685,3390,3384,2781,2165,2016,2000;2000,2002,2043,2271,2668,2668,2277,2049,2003,2000;2000,2000,2004,2027,2067,2067,2027,2004,2000,2000];
x=0:200:1800;
y=x'
surf(x,y,z);

如上图，未经二维插值处理的图像表面很粗糙。

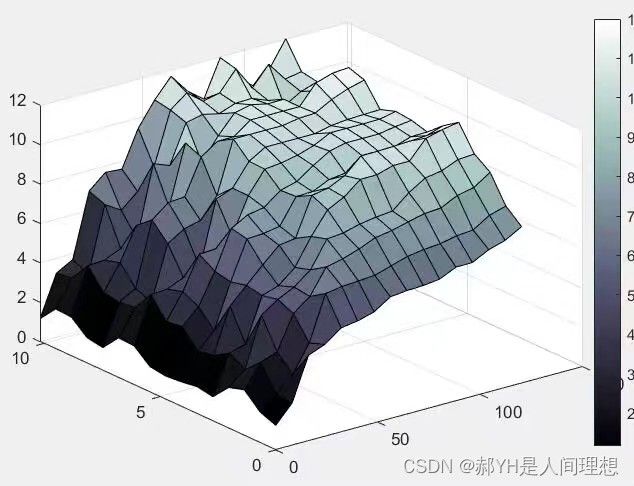
x1=0:100:1800;
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
surf(x1,y1,z1)

 

而经过插值处理后， 表面变得光滑。

如上图，进一步提高插值精度（为上一张的2倍精度），表面变得更加光滑。

 再来看另一个例子，如下图是一个关于油耗数值的散点图：

经过插值处理，三维图变得光滑（数据找不到了唉~，大家只要会套用代码就行）

x1=10:1:120;
n1=interp1(x,y1,x1,'spline');
n2=interp1(x,y2,x1,'spline');
n3=interp1(x,y3,x1,'spline');


figure(1)
plot(x1,n1);
hold on
plot(x1,n2);
hold on
plot(x1,n3);
hold off