MATLAB实现TopSis优劣解距离法——分析《世界征服者3》将领排名
问题背景
世界征服者3游戏中有150+的将领角色,每个将领都有自己的兵种优势、军阶、技能等不同的属性,如何教务客观、综合全面地选拔出其中排名前50的将领?基于TOPSIS优劣解距离法以及聚类算法,给出大家较为客观的排名。
一.问题描述
在世界征服者3游戏中,共有来自多个国家超过150位将领。游戏以全世界为地图进行战争游戏,在占领城市的过程中消灭敌军、支援友军,共有步兵、坦克、炮兵、空军、海军五大军种,此外不同将领的军阶、指挥部队的机动能力也不尽相同,将领们的技能也各有千秋。那么如何可以得到一个比较客观综合的排名顺序呢?
二.模型建立
考虑到在多指标中选择最优方案,简单做法是AHP层次分析法,但该方法过于主观,在较复杂的影响因素之下,不利于得到客观公正的结果。因此此处选择较为公平合理、且能充分利用原始数据信息的优劣解距离法——TOPSIS,来计算较为客观公正的将领得分。在将领数据已知的情况下,我们使用TOPSIS优劣解距离法可以更为客观的给出排名。
三.TOPSIS计算将领综合得分
1.确定评价将领优劣的指标:
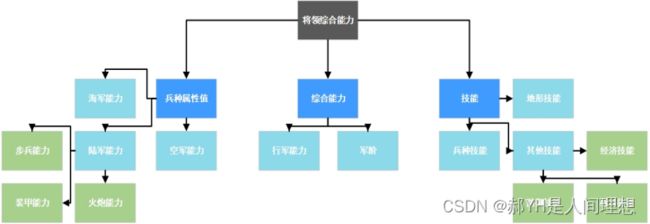
评价一个将领强悍与否,与属性加成、技能、HP值等很多因素有关,具体可以体现在以下层次图中:
综合上图,由于指标个数较多,且之间的相关性错综复杂,因此在计算大致得分时,逐一考虑并不现实,所用在第一步中大致计算得分的过程中,选择如下几个指标:
- 对于兵种属性值,由于兵种属性太多,且不同的兵种之间的优劣无法直接比较,我们在这里去兵种属性的最高值、总和两个指标来衡量,保证按照复合属性排名的准确性。
- 对于两个综合能力,则直接作为影响指标考虑。
- 对于技能,直接按照技能等级之和来进行第一步考虑。
故,在本次TOPSIS方法中,影响指标有如下5项:
| 指标 |
| 兵种最高属性点数 |
| 兵种属性总和 |
| 行军能力 |
| 军阶 |
| 技能点数之和 |
全部将领的指数在附录部分,此处仅给出一部分数据,全部数据在附录之中。(直接按照国籍划分)
| ID |
姓名 |
国籍 |
最强兵种 |
最强属性值 |
属性总和 |
行军能力 |
军阶 |
技能点数和 |
| 1 |
蒙哥马利 |
英国 |
装甲 |
4 |
14 |
3 |
280 |
14 |
| 2 |
道丁 |
英国 |
空军 |
5 |
8 |
1 |
230 |
9 |
| 3 |
亚历山大 |
英国 |
火炮 |
4 |
9 |
0 |
200 |
6 |
| 4 |
斯利姆 |
英国 |
步兵 |
4 |
10 |
2 |
170 |
8 |
| 5 |
坎宁安 |
英国 |
海军 |
5 |
10 |
0 |
140 |
8 |
| 6 |
蒙巴顿 |
英国 |
海军 |
3 |
8 |
2 |
170 |
7 |
| 7 |
韦维尔 |
英国 |
装甲 |
3 |
7 |
2 |
120 |
5 |
2.正向化处理
结合TOPSIS的思想,我们首先要对指标类型进行判断,根据分析不难得知,上述6个指标均为极大型指标(效益型指标),即,数值本身越大则代表越好。
故此处不需要对指标进行正向化处理。
3.标准化处理
此外,考虑到6个指标的单位不尽相同,此处采用标准化处理的方式,去除量纲的影响。
具体过程如下:
此处通过MATLAB进行计算,代码在附录中,结果保留5位小数,得到的数据结果在附件中,此处不一一给出。
4.计算得分
完成正向化和标准化处理后,通过MATLAB对数据矩阵进行得分计算。
通过上述方法,计算出155位将领的得分,并进行全排名,结果如下(仅展示前10名):
| 排名 |
ID |
姓名 |
国籍 |
最强兵种 |
| 1 |
24 |
曼施坦因 |
德国 |
装甲 |
| 2 |
115 |
艾森豪威尔 |
美国 |
海军 |
| 3 |
75 |
朱可夫 |
苏联 |
火炮 |
| 4 |
116 |
麦克阿瑟 |
美国 |
步兵 |
| 5 |
117 |
巴顿 |
美国 |
装甲 |
| 6 |
138 |
山下奉文 |
日本 |
步兵 |
| 7 |
1 |
蒙哥马利 |
英国 |
装甲 |
| 8 |
26 |
隆美尔 |
德国 |
装甲 |
| 9 |
25 |
古德里安 |
德国 |
装甲 |
| 10 |
27 |
邓尼茨 |
德国 |
海军 |
至此,通过TOPSIS计算将领的大致排名步骤均已完成。
5.局限性
仅仅用TOPSIS处理150位将领的排名还非常牵强,考虑到实际影响因素之多,靠TOPSIS中的六种指标给出的150+的全排名非常具有局限性。
四.实现代码
%注意:老问题,直接导入的数据总是table型
%而并非Double型的矩阵
X1=[4,14,3,280,14;5,8,1,230,9;4,9,0,200,6;4,10,2,170,8;5,10,0,140,8;3,8,2,170,7;3,7,2,120,5;3,6,1,80,6;4,7,1,80,5;3,7,1,100,4;3,4,0,35,8;2,5,1,50,4;3,6,1,50,5;2,5,1,65,3;2,6,1,35,3;3,5,2,50,3;2,7,0,230,7;3,9,2,140,5;3,9,0,200,6;2,7,1,120,6;2,5,1,140,5;3,7,1,80,2;2,5,1,35,3;5,16,5,280,18;5,11,4,170,17;5,13,3,200,17;5,10,4,200,17;4,12,3,140,13;5,13,2,230,7;5,12,2,280,11;4,13,1,170,11;5,10,1,140,10;4,10,1,200,7;4,10,2,120,10;4,11,2,140,7;4,10,3,100,4;4,8,2,100,10;4,7,1,120,8;4,9,1,80,5;3,7,2,65,5;3,6,1,100,7;2,6,1,50,6;3,5,2,65,3;2,6,2,120,2;2,6,1,50,3;4,7,0,65,2;2,3,0,35,6;3,3,0,35,4;2,4,1,80,3;4,11,0,230,8;4,6,2,170,8;4,7,2,100,8;3,9,1,80,6;2,7,1,35,2;2,6,0,35,2;3,4,0,35,4;5,9,2,200,12;2,8,0,170,9;2,4,0,120,4;3,8,0,65,4;3,4,1,50,3;2,5,0,65,7;3,5,0,80,4;2,3,2,35,4;3,5,1,80,1;2,5,0,50,4;2,6,0,35,2;2,3,0,50,4;2,3,0,35,4;2,6,0,65,3;2,4,0,65,2;2,4,0,50,2;2,4,0,35,2;1,3,0,35,3;5,17,3,280,19;4,11,4,280,11;5,10,3,170,14;4,9,5,230,7;4,10,2,200,10;5,10,1,200,10;5,8,1,120,11;5,7,1,120,9;3,9,2,140,7;3,5,4,100,6;3,9,2,120,5;3,6,1,50,5;3,7,2,80,3;3,7,1,65,3;3,7,0,65,4;3,6,1,35,3;2,5,1,35,3;3,4,0,35,3;1,3,0,35,2;2,2,1,35,2;5,9,1,200,7;3,7,4,170,10;3,7,3,140,11;2,7,1,230,12;3,7,4,170,8;3,10,4,120,9;4,7,3,120,11;3,5,1,230,8;4,8,3,100,8;4,9,1,100,6;3,6,3,80,5;3,6,3,50,2;2,4,2,65,5;2,4,0,35,4;2,2,2,35,2;2,5,0,80,5;3,4,1,65,3;2,4,2,50,2;2,5,1,35,2;1,4,0,36,2;5,24,3,280,19;4,14,5,230,14;5,15,3,200,18;5,12,2,280,16;4,13,2,200,13;5,7,4,230,11;4,15,1,170,11;5,11,3,140,9;4,10,2,100,7;5,10,2,120,6;3,6,4,80,5;4,9,1,100,6;4,5,2,120,6;4,7,3,65,3;3,9,1,65,8;3,7,2,140,4;2,3,2,80,5;2,5,1,35,5;3,7,1,65,3;2,4,1,35,5;2,5,1,35,3;2,4,0,35,5;2,4,0,50,3;4,12,5,200,14;5,12,3,230,12;5,13,1,280,9;5,11,1,120,12;4,10,2,140,8;4,11,1,170,8;4,12,2,140,10;3,9,1,80,9;3,8,0,100,5;3,9,2,100,5;4,8,1,100,4;3,6,0,65,4;2,5,2,50,2;3,6,0,35,2;2,4,2,35,2;4,2,1,35,3;2,3,0,35,3;2,3,1,50,2];
Z = X1 ./ repmat(sum(X1.*X1) .^ 0.5, 155, 1);
disp('标准化矩阵 Z = ');
disp(Z);
D_P = sum(((Z - repmat(max(Z),155,1)) .^ 2 ),2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum(((Z - repmat(min(Z),155,1)) .^ 2 ),2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S);
disp(stand_S);写在最后:结果同样具有主观性,但比AHP降低很多。本贴旨在说明Topsis的原理,大家可以去下载游戏自己试着分析一下排名~