二维坐标系极角排序的应用(POJ1696)
Space Ant
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3170 | Accepted: 2029 |
Description
The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
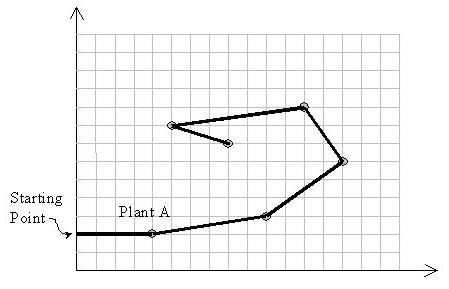
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.
- It can not turn right due to its special body structure.
- It leaves a red path while walking.
- It hates to pass over a previously red colored path, and never does that.
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.

Input
The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.
Output
Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.
Sample Input
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
题意:在二维平面坐标系中给出n个不同的点,然后一个人可以从任何点为起点,然后走下个点,保证不会向右转弯,如果连个点在一条直线上,可以一直走,问最多可以经过多少点,并输出路径?
分析:其实给出的n个点都是可以走的,首先找到y坐标最小的点,即一定是凸包上的点,然后极角排序,走排序后的第2个点,然后删除第一个点,在以刚才走的点为标志,进行极角排序,取第2个点,以此类推;
#include"string.h" #include"stdio.h" #include"iostream" #include"algorithm" #include"queue" #include"stack" #define M 1000 #define N 100009 #include"stdlib.h" #include"math.h" #define inf 10000000000000000LL #define INF 0x3f3f3f3f const double PI=acos(-1.0); #define eps 1e-10 using namespace std; struct node { double x,y; int id; node (){} node (double xx,double yy):x(xx),y(yy){} node operator -(node p) { return node (x-p.x,y-p.y); } double operator *(node p) { return x*p.y-y*p.x; } double operator ^(node p) { return x*p.x+y*p.y; } }p[M]; struct line { node s,e; int id; line(){} line(double x1,double y1,double x2,double y2) { s.x=x1; s.y=y1; e.x=x2; e.y=y2; } line(node a,node b) { s=a; e=b; } }l[M],L[M]; double max(double a,double b) { return a>b?a:b; } double min(double a,double b) { return a<b?a:b; } double cross(node a,node b,node c) { return (b-a)*(c-a); } double dot(node a,node b,node c) { return (b-a)^(c-a); } double len(node a) { return sqrt(a^a); } double dis(node a,node b) { return len(b-a); } int judge(line a,line b) { if(fabs(cross(a.s,a.e,b.s))<eps&&fabs(cross(a.s,a.e,b.e))<eps)//重合 return 1; else if(fabs((a.e-a.s)*(b.e-b.s))<eps)//平行 return -1; else return 0;//相交 } node intersection(line a,line b) { double a1=a.s.y-a.e.y; double b1=a.e.x-a.s.x; double c1=(a.e.y-a.s.y)*a.s.x+a.s.y*(a.s.x-a.e.x); double a2=b.s.y-b.e.y; double b2=b.e.x-b.s.x; double c2=(b.e.y-b.s.y)*b.s.x+b.s.y*(b.s.x-b.e.x); node ret; ret.x=(c2*b1-c1*b2)/(a1*b2-a2*b1); ret.y=(c2*a1-c1*a2)/(a2*b1-a1*b2); return ret; } int paichi(line a,line b)//快速排斥,若通过快速排斥进行跨立实验,否则无交点; { if(max(a.e.x,a.s.x)>=min(b.s.x,b.e.x) &&max(b.s.x,b.e.x)>=min(a.s.x,a.e.x) &&max(a.s.y,a.e.y)>=min(b.s.y,b.e.y) &&max(b.s.y,b.e.y)>=min(a.s.y,a.e.y)) return 1; else return 0; } int kuali(line a,line b)//跨立实验(通过相互跨立则可确定两线段相交返回1) { if(cross(a.s,a.e,b.s)*cross(a.s,a.e,b.e)<eps &&cross(b.s,b.e,a.s)*cross(b.s,b.e,a.e)<eps) return 1; return 0; } int cmp(node a,node b)//极角排序 { double temp=cross(p[0],a,b);//逆时针排序 if(temp>0) return 1; else if(fabs(temp)<eps&&dis(p[0],a)<dis(p[0],b))//角度相同则按照距离排序 return 1; else return 0; } int main() { int n,i,a; int T; cin>>T; while(T--) { scanf("%d",&n); int nn=n; node start(INF,INF); int id; for(i=0;i<n;i++) { scanf("%d%lf%lf",&a,&p[i].x,&p[i].y); p[i].id=a; if(start.y>p[i].y||(fabs(start.x-p[i].x)<eps&&start.x>p[i].x)) { start=p[i]; id=i; } } p[id]=p[0]; p[0]=start; queue<int>q; q.push(start.id); while(n>1) { sort(p+1,p+n,cmp); q.push(p[1].id); //printf("%d\n",p[1].id); swap(p[0],p[n-1]); n--; swap(p[0],p[1]); } printf("%d",nn); while(!q.empty()) { printf(" %d",q.front()); q.pop(); } printf("\n"); } }