LeetCode 刷题记录——从零开始记录自己一些不会的
1. 最多可以摧毁的敌人城堡数目
- 题意
- 思路
两层循环,太low了
用一个变量记录前一个位置
- 代码
class Solution {
public:
int captureForts(vector<int>& forts) {
int ans = 0, pre = -1;
for (int i = 0; i < forts.size(); i++) {
if (forts[i] == 1 || forts[i] == -1) {
if (pre >= 0 && forts[i] != forts[pre]) {
ans = max(ans, i - pre - 1);
}
pre = i;
}
}
return ans;
}
};
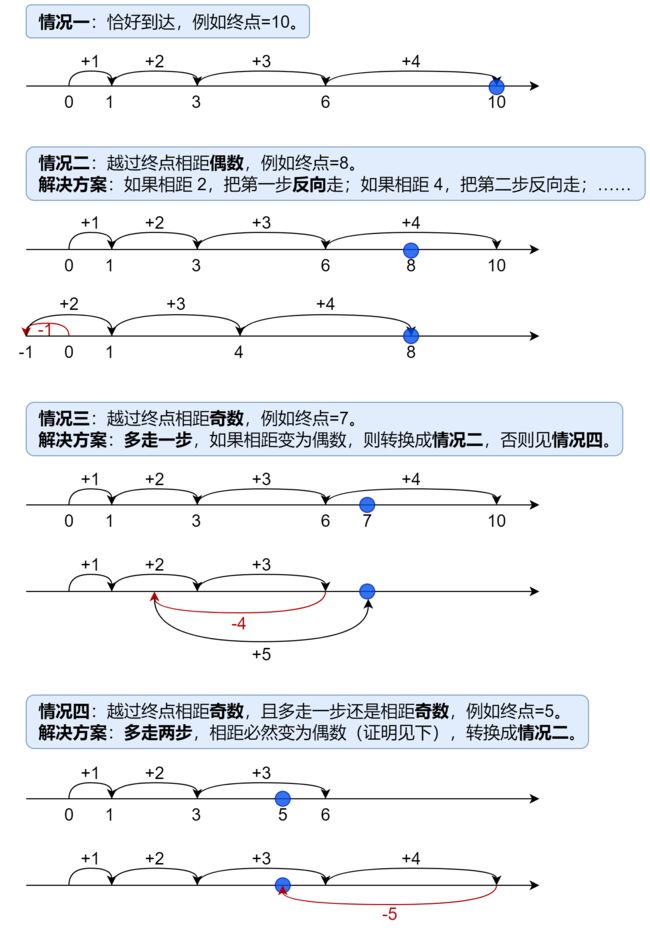
2. 到达终点的数字
- 题意
- 思路
- 代码
class Solution {
public:
int reachNumber(int target) {
target = abs(target);
int s = 0, n = 0;
while (s < target || (s - target) % 2) // 没有到达(越过)终点,或者相距奇数
s += ++n;
return n;
}
};
3. 单词的压缩编码
- 题意
- 思路
- 代码
class Solution {
public:
int minimumLengthEncoding(vector<string>& words) {
unordered_set<string> good(words.begin(), words.end());
for (const string& word: words) {
for (int k = 1; k < word.size(); ++k) {
good.erase(word.substr(k));
}
}
int ans = 0;
for (const string& word: good) {
ans += word.size() + 1;
}
return ans;
}
};
- 思路2
去找到是否不同的单词具有相同的后缀,我们可以将其反序之后插入字典树中。例如,我们有 “time” 和 “me”,可以将 “emit” 和 “em” 插入字典树中。
然后,字典树的叶子节点(没有孩子的节点)就代表没有后缀的单词,统计叶子节点代表的单词长度加一的和即为我们要的答案。
- 代码
class TrieNode{
TrieNode* children[27];
public:
int count;
TrieNode() {
for (int i = 0;i < 26;i ++)
children[i] = NULL;
count = 0;
}
TrieNode* get(char c) {
if (children[c-'a'] == NULL) {
children[c-'a'] = new TrieNode();
count ++;
}
return children[c-'a'];
}
};
class Solution{
public:
int minimumLengthEncoding(vector<string>& words) {
TrieNode* trie = new TrieNode();
unordered_map<TrieNode*,int> nodes;
for (int i = 0;i < (int)words.size();i ++) {
string word = words[i];
TrieNode* cur = trie;
for (int j = word.length()-1;j >= 0;j --)
cur = cur->get(word[j]);
nodes[cur] = i;
}
int ans = 0;
for (auto& [node,idx] : nodes) {
if (node->count == 0) {
ans += words[idx].length() + 1;
}
}
return ans;
}
};
字典树
4. 逃脱阻碍着
- 题意
- 思路
另:
- 代码
class Solution {
public:
int manhattanDistance(vector<int>& point1, vector<int>& point2) {
return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1]);
}
bool escapeGhosts(vector<vector<int>>& ghosts, vector<int>& target) {
vector<int> source(2);
int distance = manhattanDistance(source, target);
for (auto& ghost : ghosts) {
int ghostDistance = manhattanDistance(ghost, target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
};
5. 寻找两个正序数组的中位数 O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n))
- 题意
- 思路
主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
这里的 “/” 表示整除
s1 中小于等于 pivot1 的元素有 nums1[0 … k/2-2] 共计 k/2-1 个
- nums2 中小于等于 pivot2 的元素有 nums2[0 … k/2-2] 共计 k/2-1 个
ivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个- 这样 pivot 本身最大也只能是第 k-1 小的元素
pivot = pivot1,那么 nums1[0 … k/2-1] 都不可能是第 k 小的元素。把这些元素全部 “删除”,剩下的作为新的 nums1 数组- 如果 pivot = pivot2,那么 nums2[0 … k/2-1] 都不可能是第 k 小的元素。把这些元素全部 “删除”,剩下的作为新的 nums2 数组
们 “删除” 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
- 代码
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m) {
return nums2[index2 + k - 1];
}
if (index2 == n) {
return nums1[index1 + k - 1];
}
if (k == 1) {
return min(nums1[index1], nums2[index2]);
}
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
};
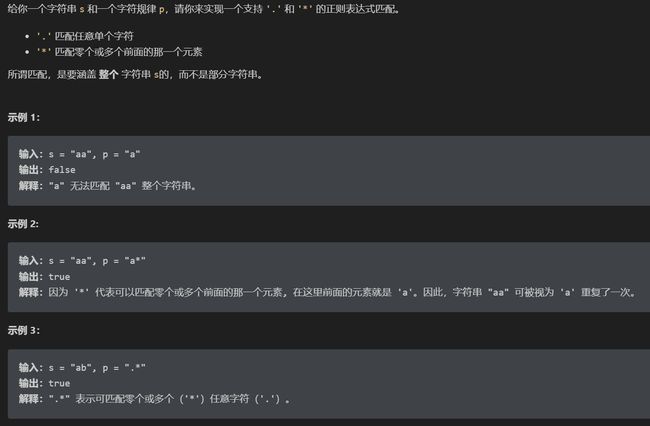
6. 正则表达式匹配
- 题意
- 思路
点号通配符其实很好实现,
s中的任何字符,只要遇到.通配符,无脑匹配就完事了。主要是这个星号通配符不好实现,一旦遇到*通配符,前面的那个字符可以选择重复一次,可以重复多次,也可以一次都不出现,这该怎么办?对于这个问题,答案很简单,对于所有可能出现的情况,全部穷举一遍,只要有一种情况可以完成匹配,就认为
p可以匹配s。那么一旦涉及两个字符串的穷举,我们就应该条件反射地想到动态规划的技巧了。
- 代码
待补
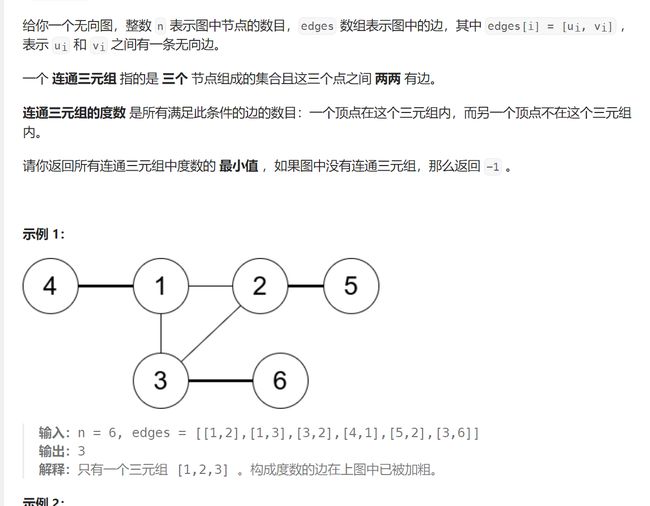
7. 一个图中联通三元组的最小度数
- 题意
待补
8. 只出现一次的数字Ⅱ 位运算
- 题意
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
- 思路
- 代码
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = 0;
for (int i = 0; i < 32; ++i) {
int total = 0;
for (int num: nums) {
total += ((num >> i) & 1);
}
if (total % 3) {
ans |= (1 << i);
}
}
return ans;
}
};
9. 数字范围按位与
- 题意
给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。
- 思路
m和n的二进制串的最长公共前缀
- 代码
class Solution {
public:
int rangeBitwiseAnd(int m, int n) {
while (m < n) {
// 抹去最右边的 1
n = n & (n - 1);
}
return n;
}
};
Brian Kernighan 算法
10. 阶乘后的零
- 题意
- 思路
- 代码
class Solution {
public:
int trailingZeroes(int n) {
int ans = 0;
while (n) {
n /= 5;
ans += n;
}
return ans;
}
};
11. 最深叶节点的最近公共祖先
- 题意
给你一个有根节点 root 的二叉树,返回它最深的叶节点的最近公共祖先。
- 思路
- 代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
pair<TreeNode*,int> f(TreeNode* root) {
if (!root) {
return {root,0};
}
auto left = f(root->left);
auto right = f(root->right);
if (left.second > right.second) {
return {left.first,left.second+1};
}
if (left.second < right.second) {
return {right.first,right.second+1};
}
return {root,left.second+1};
}
TreeNode* lcaDeepestLeaves(TreeNode* root) {
return f(root).first;
}
};
12. 连续整数求和
- 题意
- 思路
- 代码
class Solution {
public:
int consecutiveNumbersSum(int n) {
int ans = 0;
int bound = 2 * n;
for (int k = 1; k * (k + 1) <= bound; k++) {
if (isKConsecutive(n, k)) {
ans++;
}
}
return ans;
}
bool isKConsecutive(int n, int k) {
if (k % 2 == 1) {
return n % k == 0;
} else {
return n % k != 0 && 2 * n % k == 0;
}
}
};
13. 构造最长非递减子数组
- 题意
- 思路
动态规划
- 代码
class Solution {
public:
int maxNonDecreasingLength(vector<int>& nums1, vector<int>& nums2) {
int ans = 1, n = nums1.size();
vector<vector<int>> dp(n, vector<int>(2, 1));
for (int i = 1; i < n; ++i) {
if (nums1[i] >= nums1[i-1]) dp[i][0] = dp[i-1][0] + 1;
if (nums1[i] >= nums2[i-1]) dp[i][0] = max(dp[i][0], dp[i-1][1] + 1);
if (nums2[i] >= nums1[i-1]) dp[i][1] = dp[i-1][0] + 1;
if (nums2[i] >= nums2[i-1]) dp[i][1] = max(dp[i][1], dp[i-1][1] + 1);
ans = max(ans, max(dp[i][0], dp[i][1]));
}
return ans;
}
};
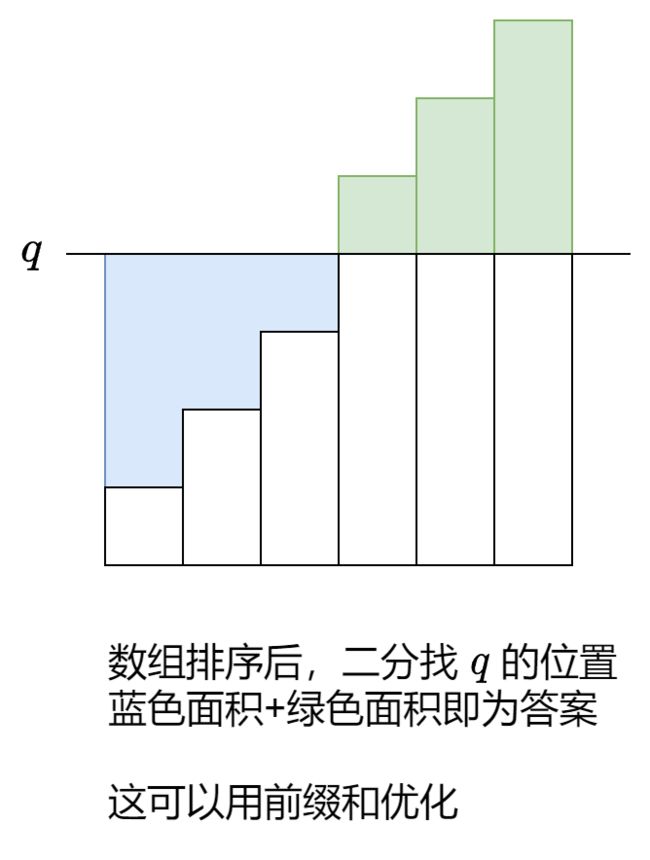
14. 等值距离和
- 题意
- 思路
分组+前缀和
- 代码
class Solution {
public:
vector<long long> distance(vector<int> &nums) {
int n = nums.size();
unordered_map<int, vector<int>> groups;
for (int i = 0; i < n; ++i)
groups[nums[i]].push_back(i); // 相同元素分到同一组,记录下标
vector<long long> ans(n);
long long s[n + 1];
s[0] = 0;
for (auto &[_, a]: groups) {
int m = a.size();
for (int i = 0; i < m; ++i)
s[i + 1] = s[i] + a[i]; // 前缀和
for (int i = 0; i < m; ++i) {
long long target = a[i];
long long left = target * i - s[i]; // 蓝色面积
long long right = s[m] - s[i] - target * (m - i); // 绿色面积
ans[target] = left + right;
}
}
return ans;
}
};
15. 使数组元素全部相等的最少操作次数
- 题意
- 思路
- 代码
class Solution {
public:
vector<long long> minOperations(vector<int> &nums, vector<int> &queries) {
sort(nums.begin(), nums.end());
int n = nums.size();
long long sum[n + 1]; // 前缀和
sum[0] = 0;
for (int i = 0; i < n; ++i)
sum[i + 1] = sum[i] + nums[i];
int m = queries.size();
vector<long long> ans(m);
for (int i = 0; i < m; ++i) {
int q = queries[i];
long long j = lower_bound(nums.begin(), nums.end(), q) - nums.begin();
long long left = q * j - sum[j]; // 蓝色面积
long long right = sum[n] - sum[j] - q * (n - j); // 绿色面积
ans[i] = left + right;
}
return ans;
}
};