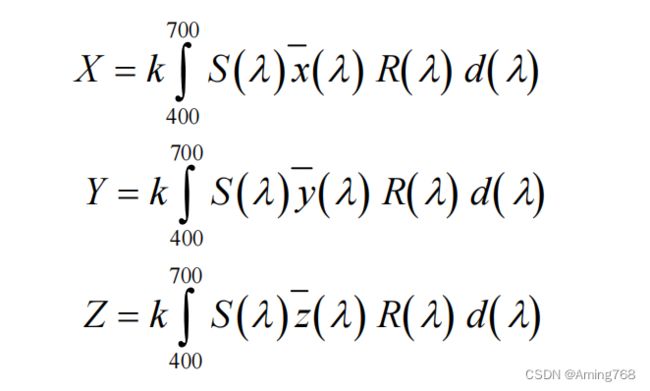2023 华数杯全国大学生数学建模竞赛B题详解
目录
一、问题背景及要求
二、问题分析
1、问题一(线性拟合)
2、问题二(单目标优化模型)
3、问题三(多目标优化模型)
4、问题四(多目标优化模型)
三、模型建立与求解
1、问题一(线性拟合)
a )数据分析
2、问题二(单目标优化模型)
3、问题三(多目标优化模型)
4、问题四(多目标优化模型)
一、问题背景及要求
日常生活中五彩缤纷的不透明有色制品是由着色剂染色而成。因此,不透明制品的配色对其外观美观度和市场竞争力起着重要作用。然而,传统的人工配色存在一定的局限性,如主观性强、效率低下等。因此,研究如何通过计算机方法来实现不透明制品的配色具有重要意义。
光通过物体传播有吸收、反射和透射三种方式。对于不透明制品来说,大部分光线会被其表面吸收或反射。吸收和反射的光线在经过透明度等校正后按波长分解成不同的颜色成分,形成光谱图。该光谱图通常由 400–700nm 波段的各色光组成。为简化计算,最终配色后的颜色的反射率以 20nm 为间隔的光谱数据来表示。对于不透明材料而言,吸收系数 K/散射系数 S 的比值与反射率 R 之间存在一定关系,具体请参考文献【1】《计算机配色理论及算法的研究》中的 K-M光学模型。
基于光学模型得到的颜色参数,可应用于色差的计算。通常,使用色差(不超过 1)来作为配色效果好坏的标准。色差计算方法参考文献【2】《基于 CIELAB均匀颜色空间和聚类算法的混纺测色研究》中的 CIELAB 色彩空间的总色差计算方法。其中颜色参数 L*(明度)、a*(红绿色度)和 b*(黄蓝色度)计算中出现的三刺激值 XYZ 的计算方法如下:
其中, S ( λ ) 为光谱能量分布,![]() 为观察者光谱三刺激值,S ( λ ) 分别与x ( λ ) , y ( λ ) ,z ( λ ) 相乘为固定值见附件 1。R ( λ ) 为光谱反射率,k值约为 0.1,d ( λ )为测量物体反射率波长间隔,本题d(λ) =20nm。
为观察者光谱三刺激值,S ( λ ) 分别与x ( λ ) , y ( λ ) ,z ( λ ) 相乘为固定值见附件 1。R ( λ ) 为光谱反射率,k值约为 0.1,d ( λ )为测量物体反射率波长间隔,本题d(λ) =20nm。
不透明制品配色问题,就是基于光学模型,设计不透明制品的配色模型。相较于人工配色,节省大量人力、物力和财力,对减少能耗具有重要意义。
针对某一不透明制品,已知红、黄、蓝 3 种着色剂在不同浓度不同波长的 K/S 值以及基底材料在不同波长下的 K/S 值,见附件 2。其中,浓度=着色剂克重/基材重量。每个着色剂的吸收系数 K/散射系数 S 的比值具有加和性,详见文献【1】《计算机配色理论及算法的研究》中的 K-M 单常数理论。现有 10 个目标样(二到三种着色剂混合制成)的 R 值,见附件 3。结果展示请保留 4 位小数。
请建立数学模型解决如下几个问题:
问题 1:请分别计算附件 2 中三种着色剂在不同波长下 K/S 与浓度的关系,并将关系式与拟合系数填写在表格中。
问题 2:请建立不透明制品配色的优化模型。在已知目标样的 R 值(附件 3)的前提下,基于光谱三刺激值加权表(附件 1)与着色剂 K/S 基础数据库(附件 2),运用优化模型配出与目标样的色差最为接近的 10 个不同配方,要求色差小于 1。
问题 3:在问题 2 的基础上,考虑成本控制和批量配色,改进配色模型。对 2kg 的基底材料进行配色,求出与目标样(附件 3)之间色差最为接近的 10 个不同配方,要求色差小于 1。色母粒单位克重价格见附件 4。
问题 4:在实际生产中,配色所需要的着色剂越少越好,基于此,在问题 3的基础上,寻找附件 3 中前 5 个样本的最优的配色方案,要求每个样本配出 5个不同的配方且色差小于 1。
二、问题分析
1、问题一(线性拟合)
2、问题二(单目标优化模型)
3、问题三(多目标优化模型)
4、问题四(多目标优化模型)
问题四在问题三的基础上,进一步考虑着色剂数量。
三、模型建立与求解
1、问题一(线性拟合)
a )数据分析
为了获得三种着色剂在不同波长下 K/S 与浓度的函数关系式,我们首先需要判断不同波长下 K/S 与浓度的关系为线性还是非线性。因此,我们基于附件二中给出的三种着色剂在不同波长下/值与浓度关系的数据进行可视化得下图:
b )模型建立与求解
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
df = pd.read_excel('附件2.xlsx')
X = np.array([0.05, 0.1, 0.5, 1.0, 2.0, 3.0, 4.0, 5.0])
X = X.reshape(-1, 1)
val = 400
for i in range(2, 18):
print(f"波长{val}")
print("红色")
y1 = df[df.columns[i]][2:10]
model = LinearRegression()
model.fit(X, y1)
slope = model.coef_[0]
intercept = model.intercept_
r_squared = model.score(X, y1)
slope1 = ('%.4f' % slope)
intercept1 = ('%.4f' % intercept)
print(f"K/S = {slope:.4f} C + {intercept:.4f}")
print(f"{r_squared:.4f}")将数据填入表格,问题一处理完毕。
2、问题二(单目标优化模型)
a )目标函数推导
以上公式在题目所给的参考文献中均有涉及,通过推导可得到由配方到色差的相关程序。
具体程序如下:
import openpyxl
K_Sbase = [0.039492, 0.025906, 0.017964, 0.015092,
0.011439, 0.009515, 0.007961, 0.006947,
0.006284, 0.005889, 0.005238, 0.004948,
0.004626, 0.004247, 0.004100, 0.003617] # 基材的K/S
def get_K_S(x):
wb1 = openpyxl.load_workbook("浓度与KR比值的拟合函数表.xlsx")
sheets1 = wb1.worksheets # 获取当前所有的sheet
sheet11 = sheets1[0]
cr = x[0] # cr = r/base
cy = x[1]
cb = x[2]
K_Sr = [] # 各颜色的K/S
K_Sy = []
K_Sb = []
K_S = [] # 混合色的K/S
for i in range(2, 18): # 根据浓度求K/S
k = sheet11.cell(row=i, column=2).value
k = float(k)
K_Sr.append(k)
k = sheet11.cell(row=i, column=4).value
k = float(k)
K_Sy.append(k)
k = sheet11.cell(row=i, column=6).value
k = float(k)
K_Sb.append(k)
for i in range(0, 16):
K_S.append(K_Sbase[i]+cr*K_Sr[i]+cy *
K_Sy[i]+cb*K_Sb[i]) # 求出K/S在第i波长时的值
return K_S
def get_R(K_S):
R = [] # 各波长的反射率
for i in range(0, 16):
R.append(1 + K_S[i] - (K_S[i]*K_S[i]+2*K_S[i])**(1/2))
return R
def get_XYZ(R):
wb2 = openpyxl.load_workbook("附件1.xlsx")
sheets2 = wb2.worksheets # 获取当前所有的sheet
sheet12 = sheets2[0]
X = 0
Y = 0
Z = 0
d = 20
k = 0.1
for row in range(4, 20):
SX = sheet12.cell(row=row, column=2).value
SY = sheet12.cell(row=row, column=3).value
SZ = sheet12.cell(row=row, column=4).value
X += SX * R[row-4] * d
Y += SY * R[row-4] * d
Z += SZ * R[row-4] * d
X = X * k
Y = Y * k
Z = Z * k
return X, Y, Z
def XYZ_to_Lab(X, Y, Z):
X0 = 94.83
Y0 = 100.00
Z0 = 107.38
X_X0 = X / X0
Y_Y0 = Y / Y0
Z_Z0 = Z / Z0
if X_X0 <= 0.008856 or Y_Y0 <= 0.008856 or Z_Z0 <= 0.008856:
L = 903.3 * Y_Y0
a = 3893.5 * (X_X0 - Y_Y0)
b = 1557.4 * (Y_Y0 - Z_Z0)
else:
L = 116 * pow(Y_Y0, 1 / 3) - 16
a = 500 * (pow(X_X0, 1 / 3) - pow(Y_Y0, 1 / 3))
b = 200 * (pow(Y_Y0, 1 / 3) - pow(Z_Z0, 1 / 3))
return L, a, b
def get_sample_Lab(sample):
# 获取样本的Lab
wb3 = openpyxl.load_workbook("样品Lab值.xlsx")
sheets3 = wb3.worksheets # 获取当前所有的sheet
sheet13 = sheets3[0]
L_sample = 0
a_sample = 0
b_sample = 0
L_sample = sheet13.cell(row=sample+1, column=2).value
a_sample = sheet13.cell(row=sample+1, column=3).value
b_sample = sheet13.cell(row=sample+1, column=4).value
return L_sample, a_sample, b_sample
def get_E(L, L_sample, a, a_sample, b, b_sample):
# 计算色差
# 明度差
Ls_L = L_sample - L
# 饱和度差
Cs = pow(a_sample*a_sample+b_sample*b_sample, 1/2)
C = pow(a*a+b*b, 1/2)
Cs_C = Cs-C
# 色度差
tmp = (a_sample-a)*(a_sample-a)+(b_sample-b)*(b_sample-b)
Cc_C = tmp**(1/2)
# 色相差
tmp = Cc_C*Cc_C-Cs_C*Cs_C
H = tmp**(1/2)
# 总色差
tmp = Ls_L*Ls_L+Cs_C*Cs_C+H*H
E = tmp**(1/2)
return E
def evaluate(x, sample):
K_S = get_K_S(x)
R = get_R(K_S)
X, Y, Z = get_XYZ(R)
L, a, b = XYZ_to_Lab(X, Y, Z)
L_sample, a_sample, b_sample = get_sample_Lab(sample)
E = get_E(L, L_sample, a, a_sample, b, b_sample)
# print(E)
return E
# evaluate([1, 1, 1], 1)
b )模型建立与求解
由于这是单目标优化问题,我们采用SLSQP 算法求解,可用网格化的方法,在在[0.05,5]的浓度区间设置猜测值,不断进行二次规划,最后当约束条件与结果达到目标精度或到达最大迭代次数时,停止优化迭代。
计算得到的部分解如下:
3、问题三(多目标优化模型)
a )目标函数
由于问题三在问题二的基础上进一步考虑成本控制和批量配色,因此我们加入计算价格的cost()函数:
def cost(x):
return 60*x[0]+65*x[1]+63*x[2]目标函数数学描述如下:
b )模型建立与求解
# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea
import rate_to_E_problem3
"""
问题类定义
"""
size =200
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 2 # 初始化M(目标维数)
maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 3 # 初始化Dim(决策变量维数)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [0] * Dim # 决策变量下界
ub = [1] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界
ubin = [1] * Dim # 决策变量上边界
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def aimFunc(self, pop): # 目标函数
x1 = pop.Phen[:, [0]]
x2 = pop.Phen[:, [1]]
x3 = pop.Phen[:, [2]]
pop.ObjV = np.zeros((pop.Phen.shape[0], self.M))
ans1=np.empty([size,1])
ans2=np.empty([size,1])
k = x1**4-10*x1**2+x1*x2+x2**4-x1**2*x2**2
t = k.shape[0]
for i in range(0,t):
ans1[i][0]=rate_to_E_problem3.evaluate_E([x1[i][0],x2[i][0],x3[i][0]],6)
for i in range(0,t):
ans2[i][0]=rate_to_E_problem3.cost([x1[i][0],x2[i][0],x3[i][0]])
pop.ObjV[:,[0]] = ans1
pop.ObjV[:,[1]] = ans2
"""
执行脚本
"""
if __name__ == '__main__':
problem = MyProblem() # 生成问题对象
# 构建算法
algorithm = ea.moea_NSGA2_templet(problem,
ea.Population(Encoding='RI', NIND=size),
MAXGEN=80, # 最大进化代数。
logTras=0) # 表示每隔多少代记录一次日志信息,0表示不记录。
# 求解
algorithm.mutOper.Pm = 0.2 # 修改变异算子的变异概率
algorithm.recOper.XOVR = 0.9 # 修改交叉算子的交叉概率
res = ea.optimize(algorithm, verbose=False, drawing=0, outputMsg=True, drawLog=False, saveFlag=False, dirName='result')
# print(res)
# print(res['hv'])
# print(res['spacing'])
wb1 = openpyxl.load_workbook("问题三数据.xlsx")
sheets1 = wb1.worksheets # 获取当前所有的sheet
sheet11 = sheets1[5]
tmpphen = res['optPop'].Phen
tmpobvj = res['optPop'].ObjV
sheet11.cell(row=2, column=4).value = res['hv']
sheet11.cell(row=2, column=5).value = res['spacing']
ii = 2
for i in range(0,tmpobvj.shape[0]):
tmpphen[i][0] = ('%.4f' % tmpphen[i][0])
tmpphen[i][1] = ('%.4f' % tmpphen[i][1])
tmpphen[i][2] = ('%.4f' % tmpphen[i][2])
tmpobvj[i][0]=('%.4f' % tmpobvj[i][0])
tmpobvj[i][1] = ('%.4f' % tmpobvj[i][1])
if tmpobvj[i][0]< 1:
tmp = '[{},{},{}]'.format(tmpphen[i][0],tmpphen[i][1],tmpphen[i][2])
sheet11.cell(row=ii, column=1).value=tmp
sheet11.cell(row=ii, column=2).value = tmpobvj[i][0]
sheet11.cell(row=ii, column=3).value = tmpobvj[i][1]
ii+=1计算得到的问题三样本一部分配方如下:
4、问题四(多目标优化模型)
问题四在问题三的基础上,进一步考虑着色剂数量。因此,加入目标函数:着色剂数量,并对问题三相关代码进行相应修改,即可获得问题四答案。
计算得到的问题三样本一部分配方如下:
四、后记
缺点:1、问题三中模型求解相关代码在种群数目和迭代次数增加时运行时间较长(种群200,迭代次数80下要跑将近20分钟)。
2、我们使用的色差计算方法与专家点评中的计算方法存在出入,因此数据结果上可能存在偏差,但是方法上各位可以大胆借鉴(获奖了)!!
解决方法:1、多进程同时跑,但是电脑负载较大。
2、可进行相应优化,经过优化后的代码,速度可跃升到5s(同样种群200,迭代次数80)
如有问题,恳请各位能提出批评建议,不胜感激。
如有疑惑,也欢迎私聊博主。