机器学习——逻辑回归(LR)
机器学习——逻辑回归(LR)
文章目录
- 前言
- 一、原理介绍
- 二、代码实现
-
- 2.2. 混淆矩阵
- 2.3. 分类报告
- 2.4. 可视化分类结果
- 三、额外(先划分数据集再降维与先降维再划分数据集)
-
- 3.1. 先划分数据集再降维
- 3.2. 先降维再划分数据集
- 3.3. 比较
- 总结
前言
在机器学习的分类算法中,逻辑回归是一个基础的分类算法,本文将简单介绍一下逻辑回归算法。
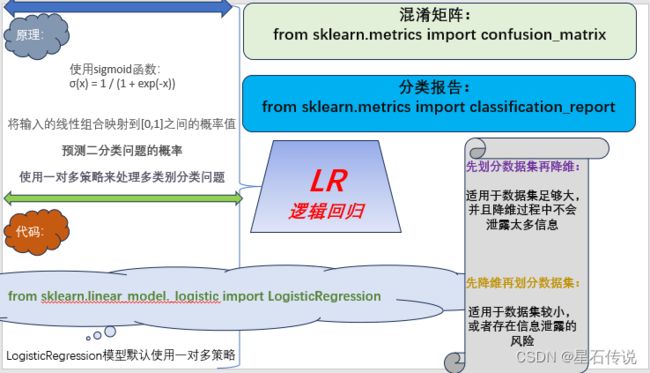
一、原理介绍
尽管名字中带有"回归"这个词,但逻辑回归其实是一种用于分类问题的算法,而不是回归问题。
逻辑回归是一种广义线性模型,它通过使用逻辑函数(也称为sigmoid函数)将输入的线性组合映射到[0,1]之间的概率值,用于预测二分类问题的概率。在逻辑回归中,我们根据预测的概率值来判断样本属于哪个类别。 σ(x) = 1 / (1 + exp(-x))
通常情况下,我们将概率大于等于阈值的样本划分为正类,将概率小于阈值的样本划分为负类(阈值可自行设置,一般情况下为0.5)
然而,逻辑回归算法也可以用于多分类问题。一种常见的方法是使用一对多策略,将多分类问题转化为多个二分类问题
在sklearn库中,LogisticRegression模型默认使用一对多(OvR)策略来处理多类别分类问题。
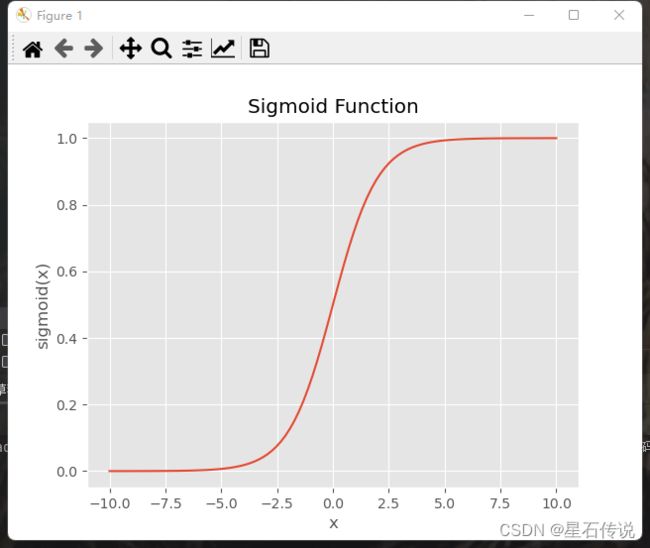
sigmoid函数图如下所示:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = sigmoid(x)
# 绘制sigmoid函数图形
plt.style.use("ggplot")
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.title('Sigmoid Function')
plt.show()
二、代码实现
使用鸢尾花数据集
#加载iris数据集
from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.3,random_state=41)
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)
#逻辑回归
from sklearn.linear_model._logistic import LogisticRegression
model = LogisticRegression(max_iter= 1000)
model.fit(x_train,y_train)
#计算分类的正确率
print(model.score(x_test,y_test))
0.8888888888888888
#查看分类的概率值
#print(model.predict_proba(x_test))
#在测试集上实现预估
y_pred = model.predict(x_test)
#print(y_pred,y_test)
2.2. 混淆矩阵
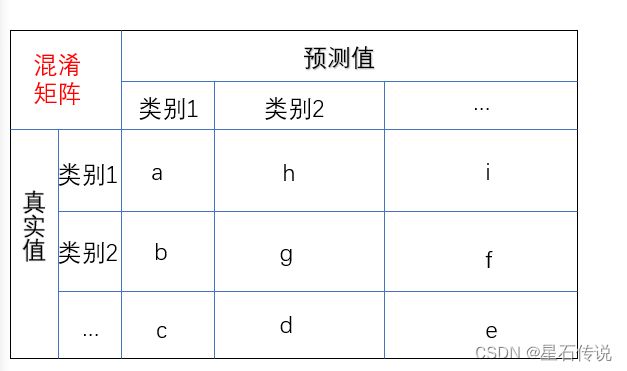
使用混淆矩阵,观察每种类别被错误分类的情况(以矩阵形式将数据集中的记录按真实的类别与分类模型预测的类别判断两个标准进行汇总)
如图所示:
例如:图中a 代表真实值为类别1,预测值也为类别1的正确分类的样本数; 图中b 代表真实值为类别2,预测值却为类别1的错误分类的样本数
#混淆矩阵
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_true=y_test,y_pred=y_pred))
[[11 0 0]
[ 0 16 2]
[ 0 3 13]]
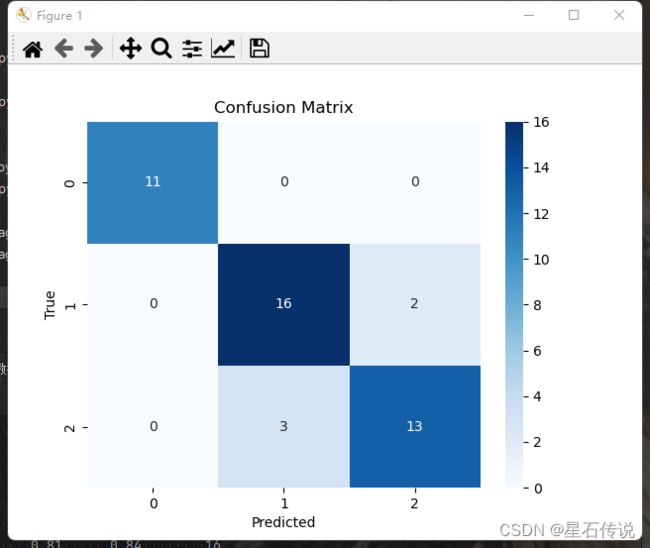
混淆矩阵的可视化
import seaborn as sns
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()
2.3. 分类报告
使用分类报告来查看一下针对每个类别的预测准确性
-
precision : 精确度,表示模型正确预测为某个类别的样本数量与所有预测为该类别的样本数量的比例
-
recall:召回率,表示模型正确预测为某个类别的样本数量与所有实际属于该类别的样本数量的比例
-
f1-score : f1分数,可视为精确度与召回率的加权平均值。取值范围为 0 到 1,越接近 1 表示模型的性能越好。F1 = (precision * recall ) / (precision + recall )
-
support:支持数量,属于某个类别的样本数量
-
accuracy:准确率,指模型在整个测试数据集上的分类正确率。即预测正确的样本数量与总样本数量的比例
-
宏平均(macro avg)和加权平均(weighted avg)
#分类报告
from sklearn.metrics import classification_report
print(classification_report(y_test,y_pred,target_names= iris["target_names"]))
precision recall f1-score support
setosa 1.00 1.00 1.00 11
versicolor 0.84 0.89 0.86 18
virginica 0.87 0.81 0.84 16
accuracy 0.89 45
macro avg 0.90 0.90 0.90 45
weighted avg 0.89 0.89 0.89 45
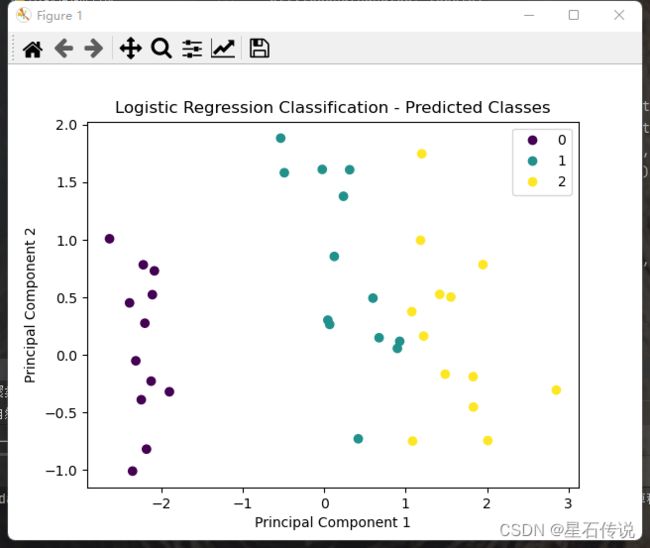
2.4. 可视化分类结果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
# 加载数据集
from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data
y = iris.target
# 数据的划分
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=20)
# 标准化
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)
# 使用PCA进行降维
pca = PCA(n_components=2)
x_train_pca = pca.fit_transform(x_train)
x_test_pca = pca.transform(x_test)
# 创建逻辑回归模型
clf = LogisticRegression()
clf.fit(x_train_pca, y_train)
# 使用模型进行预测
y_pred = clf.predict(x_test_pca)
# 绘制散点图
plt.scatter(x_test_pca[:, 0], x_test_pca[:, 1], c=y_pred)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('Logistic Regression Classification - Predicted Classes')
plt.show()
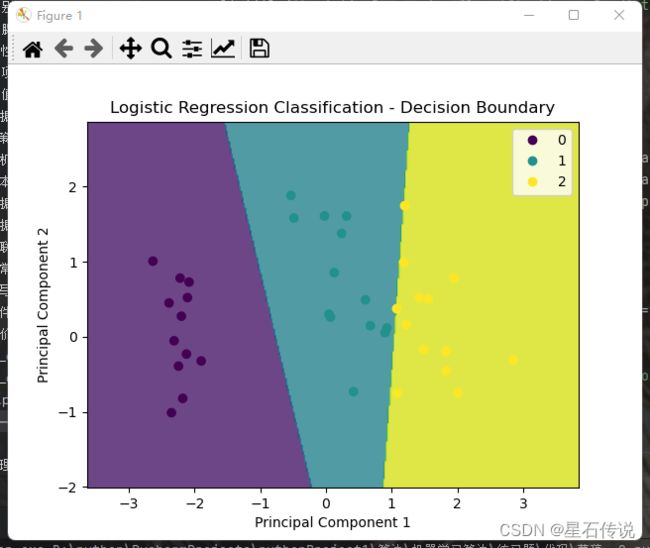
# 绘制决策边界图
h = 0.02 # 步长
x1_min, x1_max = x_test_pca[:, 0].min() - 1, x_test_pca[:, 0].max() + 1
x2_min, x2_max = x_test_pca[:, 1].min() - 1, x_test_pca[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, h), np.arange(x2_min, x2_max, h))
Z = clf.predict(np.c_[xx1.ravel(), xx2.ravel()])
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.8)
plt.scatter(x_test_pca[:, 0], x_test_pca[:, 1], c=y_pred)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('Logistic Regression Classification - Decision Boundary')
plt.show()
三、额外(先划分数据集再降维与先降维再划分数据集)
先划分数据集再降维与先降维再划分数据集这两种方法有一些区别。
3.1. 先划分数据集再降维
先划分数据集再降维:数据集首先被划分为训练集和测试集,然后在训练集上进行降维操作,然后将降维后的特征应用于测试集。
这种方法的优点是可以在训练集上学习降维的变换,并将这个变换应用于测试集,以获得测试集上的一致性。然而,这种方法可能会导致信息泄露,因为降维过程中使用了测试集的信息,可能会对模型的性能产生偏向。
3.2. 先降维再划分数据集
先降维再划分数据集:首先在整个数据集上进行降维操作,然后再将降维后的数据集划分为训练集和测试集。
这种方法的优点是可以避免信息泄露问题,因为降维过程中没有使用测试集的信息。然而,这种方法可能会**导致训练集和测试集之间的不一致性,**因为降维过程是在整个数据集上进行的,而不是在训练集上进行的。
3.3. 比较
哪种方法更好取决于具体的情况。如果数据集足够大,并且降维过程中不会泄露太多信息,那么先划分数据集再降维可能是一个更好的选择,因为可以在训练集上学习到更好的降维变换。
如果数据集较小,或者存在信息泄露的风险,那么先降维再划分数据集可能是一个更好的选择,以确保训练集和测试集之间的一致性。
最好是根据具体问题和数据集的特点进行实验和比较,选择最适合的方法。
总结
本文从逻辑回归算法的原理介绍到代码实现中的回归模型的构建以及混淆矩阵和分类报告的介绍,还有对分类结果的可视化。详细介绍了LR算法,还有最后的先划分数据集再降维还是先降维再划分数据集的讨论。
明月几时有,把酒问青天
–2023-9-5 筑基篇