球谐函数原理
参考:球谐函数极其应用
球谐函数是什么
球谐函数是傅里叶级数的高维类比,由一组表示球体表面的基函数构成。
同时,球谐函数是Laplace算子角动量在三个维度上的特征函数。
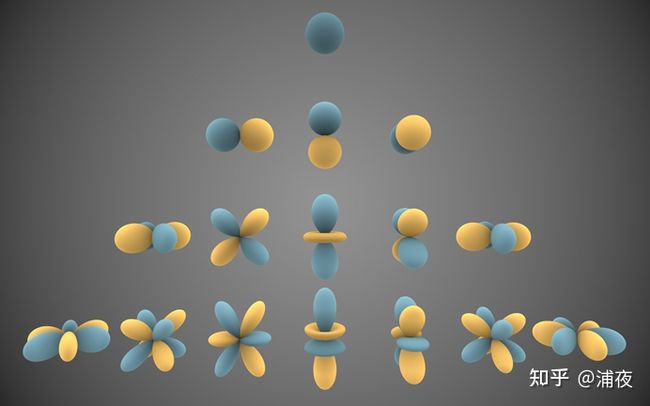
文章目录
- 球谐函数是什么
- 球坐标下的Laplace方程
-
- Laplace方程(Laplace’s equation)
- 三维直角坐标系下的Laplace方程
- 将其转化为球坐标系
- 将球坐标函数分离
- 勒让德多项式
- 连带勒让德多项式
-
- 连带勒让德多项式的前几阶表达式
- 将勒让德多项式代入球谐函数
- 球谐函数的性质
- 球谐函数的使用
- 球谐函数的实现
球坐标下的Laplace方程
Laplace方程(Laplace’s equation)
拉普拉斯算符(Laplacian) ▽ 2 \bigtriangledown^2 ▽2被定义为梯度的散度( ▽ ⋅ ▽ \bigtriangledown \cdot \bigtriangledown ▽⋅▽或 △ \bigtriangleup △ ),有点类似于单变量函数的2阶导数。
对于函数 u ( x 1 , x 2 , . . . ) u(x_1,x_2,...) u(x1,x2,...), Laplace方程为:
∑ i = 1 n ∂ 2 u ∂ x i 2 = 0 \sum_{i=1}^n{\frac{\partial^2 u}{\partial x_i^2}} = 0 i=1∑n∂xi2∂2u=0
它表示一个函数在它各个变量的二阶偏导下都为0。
在一维情况下,在如下方程中可以理解为,当函数为Laplace方程时,加速度为0.
x ( t ) = v t + 1 2 a t 2 x(t) = vt + \frac{1}{2}at^2 x(t)=vt+21at2
其他适用的场景包括:
- 室内均衡的气温的Laplacian等于0。
- 平衡水膜下受力的Laplacian等于0。
- 静电场中的电压场的Laplacian等于0。
综上,我们得出Laplacian等于0的函数可看作一种平衡状态,因此也被称为谐波函数(Harmonic)
三维直角坐标系下的Laplace方程
▽ 2 u = ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 = 0 ( 1 ) \bigtriangledown^2 u = \frac{\partial^2 u }{\partial x^2} + \frac{\partial^2 u }{\partial y^2} + \frac{\partial^2 u }{\partial z^2} =0\quad (1) ▽2u=∂x2∂2u+∂y2∂2u+∂z2∂2u=0(1)
我们要做的就是求出三维Laplace方程的通解。
将其转化为球坐标系
将如下球面坐标表示代入 ( 1 ) (1) (1)式
{ x = r sin θ cos φ y = r sin θ sin φ z = r cos θ ( 2 ) \left\{\begin{array}{c} x=r \sin \theta \cos \varphi \\ y=r \sin \theta \sin \varphi \\ z=r \cos \theta \end{array}\right. \quad (2) ⎩ ⎨ ⎧x=rsinθcosφy=rsinθsinφz=rcosθ(2)
得到
1 r 2 ∂ ∂ r ( r 2 ∂ f ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ f ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 f ∂ φ 2 = 0 ( 3 ) \frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial f}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial f}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} f}{\partial \varphi^{2}}=0\quad (3) r21∂r∂(r2∂r∂f)+r2sinθ1∂θ∂(sinθ∂θ∂f)+r2sin2θ1∂φ2∂2f=0(3)
推导原理可参照:Laplacian in Spherical Coordinates
将球坐标函数分离
u ( r , θ , ψ ) = R ( r ) Y ( θ , φ ) u(r,\theta,\psi ) = R(r)Y(\theta,\varphi) u(r,θ,ψ)=R(r)Y(θ,φ)
- R ( r ) R(r) R(r)表示距离部分
- Y ( θ , φ ) Y(\theta,\varphi) Y(θ,φ)就是球谐函数
分离后得到:
1 R d d r ( r 2 d R d r ) = − 1 sin ( θ ) Y ∂ ∂ θ ( sin ( θ ) ∂ Y ∂ θ ) − 1 Y 1 sin 2 ( θ ) ∂ 2 Y ∂ φ 2 ( 4 ) \frac{1}{R} \frac{d}{d r}\left(r^{2} \frac{d R}{d r}\right)=-\frac{1}{\sin (\theta) Y} \frac{\partial}{\partial \theta}\left(\sin (\theta) \frac{\partial Y}{\partial \theta}\right)-\frac{1}{Y} \frac{1}{\sin ^{2}(\theta)} \frac{\partial^{2} Y}{\partial \varphi^{2}}\quad\quad (4) R1drd(r2drdR)=−sin(θ)Y1∂θ∂(sin(θ)∂θ∂Y)−Y1sin2(θ)1∂φ2∂2Y(4)
方程的左边是关于R的函数,右边是关于 φ , θ \varphi,\theta φ,θ的函数,两边等式成立,需要两边都等于一个常数。
设这个常数为 l ( l + 1 ) l(l+1) l(l+1)得到两个新方程
d d r ( r 2 ∂ Y ∂ θ ) − l ( l + 1 ) R = 0 1 sin ( θ ) ∂ ∂ θ ( sin ( θ ) ∂ Y ∂ θ ) + 1 sin 2 ( θ ) ∂ 2 Y ∂ φ 2 + l ( l + 1 ) Y = 0 \begin{array}{c} \frac{d}{d r}\left(r^{2} \frac{\partial Y}{\partial \theta}\right)-l(l+1) R=0 \\ \quad\\ \frac{1}{\sin (\theta)} \frac{\partial}{\partial \theta}\left(\sin (\theta) \frac{\partial Y}{\partial \theta}\right)+\frac{1}{\sin ^{2}(\theta)} \frac{\partial^{2} Y}{\partial \varphi^{2}}+l(l+1) Y=0 \end{array} drd(r2∂θ∂Y)−l(l+1)R=0sin(θ)1∂θ∂(sin(θ)∂θ∂Y)+sin2(θ)1∂φ2∂2Y+l(l+1)Y=0
- 第一个方程是距离方程
- 第二个方程是球函数方程
我们将球面谐波函数继续分离
Y ( θ , ψ ) = Θ ( θ ) Φ ( φ ) Y(\theta,\psi) = \Theta (\theta) \Phi (\varphi) Y(θ,ψ)=Θ(θ)Φ(φ)
得到
( 1 − x 2 ) d 2 Θ d x 2 − 2 x d Θ d x + [ l ( l + 1 ) − m 2 1 − x 2 ] Θ = 0 \left(1-x^{2}\right) \frac{d^{2} \Theta}{d x^{2}}-2 x \frac{d \Theta}{d x}+\left[l(l+1)-\frac{m^{2}}{1-x^{2}}\right] \Theta=0 (1−x2)dx2d2Θ−2xdxdΘ+[l(l+1)−1−x2m2]Θ=0
这个方程是一个特殊的方程,叫做:l阶连带勒让德方程
勒让德多项式
勒让德方程:
d d x [ ( 1 − x 2 ) d d x P l ( x ) ] + l ( l + 1 ) P l ( x ) = 0 \frac{\mathrm{d}}{\mathrm{d} x}\left[\left(1-x^{2}\right) \frac{\mathrm{d}}{\mathrm{d} x} P_{l}(x)\right]+l(l+1)P_{l}(x)=0 dxd[(1−x2)dxdPl(x)]+l(l+1)Pl(x)=0
我们仅在区间 x ∈ [ − 1 , 1 ] x\in[-1,1] x∈[−1,1] 上考虑 l l l 为非负整数的情况,方程的解 P l ( x ) P_l(x) Pl(x) 是关于 x x x 的 l l l 阶多项式。
P l ( x ) = 1 2 l ∑ s = 0 [ l / 2 ] ( − 1 ) s ( 2 l − 2 s ) ! s ! ( l − s ) ! ( l − 2 s ) ! x l − 2 s P_{l}(x)=\frac{1}{2^{l}} \sum_{s=0}^{[l / 2]} \frac{(-1)^{s}(2 l-2 s) !}{s !(l-s) !(l-2 s) !} x^{l-2 s} Pl(x)=2l1s=0∑[l/2]s!(l−s)!(l−2s)!(−1)s(2l−2s)!xl−2s
也可写作
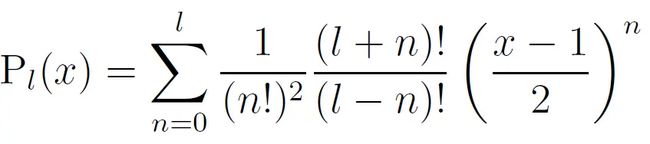
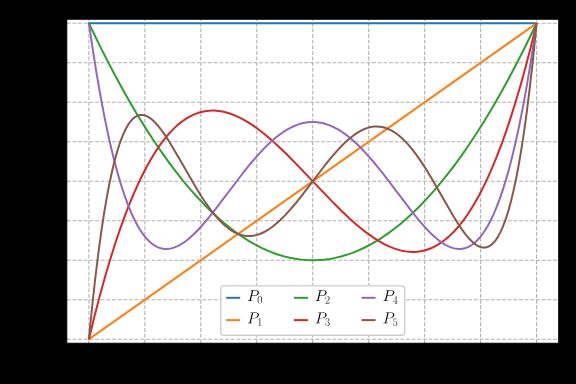
这里列出了勒让德多项式的前6项结果,其他项可以根据公式自推。
也可参照勒让德多项式的基本介绍和MATLAB绘图
P 0 ( x ) = 1 P 1 ( x ) = x P 2 ( x ) = 1 2 ( 3 x 2 − 1 ) P 3 ( x ) = 1 2 ( 5 x 3 − 3 x ) P 4 ( x ) = 1 8 ( 35 x 4 − 30 x 2 + 3 ) P 5 ( x ) = 1 8 ( 63 x 5 − 70 x 3 + 15 x ) P_0(x) = 1\\\quad\\ P_1(x) = x\\\quad\\ P_2(x) = \frac{1}{2}(3x^2-1)\\\quad\\ P_3(x) = \frac{1}{2}(5x^3-3x)\\\quad\\ P_4(x) = \frac{1}{8}(35x^4-30x^2+3)\\\quad\\ P_5(x) = \frac{1}{8}(63x^5-70x^3+15x)\\\quad\\ P0(x)=1P1(x)=xP2(x)=21(3x2−1)P3(x)=21(5x3−3x)P4(x)=81(35x4−30x2+3)P5(x)=81(63x5−70x3+15x)
勒让德多项式也可以用罗德里格斯公式表示
P l ( x ) = 1 2 l l ! d l d x l ( x 2 − 1 ) l P_l(x) = \frac{1}{2^ll!}\frac{d^l}{dx^l}(x^2-1)^l Pl(x)=2ll!1dxldl(x2−1)l
连带勒让德多项式
连带勒让德方程来源于在球坐标系中使用分离变量法解拉普拉斯方程(球坐标系中的拉普拉斯方程)中
连带勒让德方程为
d d x [ ( 1 − x 2 ) d d x P l m ( x ) ] + [ l ( l + 1 ) − m 2 1 − x 2 ] P l m ( x ) = 0. \frac{\mathrm{d}}{\mathrm{d} x}\left[\left(1-x^{2}\right) \frac{\mathrm{d}}{\mathrm{d} x} P_{l}^{m}(x)\right]+\left[l(l+1)-\frac{m^{2}}{1-x^{2}}\right] P_{l}^{m}(x)=0 . dxd[(1−x2)dxdPlm(x)]+[l(l+1)−1−x2m2]Plm(x)=0.
当 m = 0 m = 0 m=0时,该方程变为勒让德方程。
d d x [ ( 1 − x 2 ) d d x P l ( x ) ] + l ( l + 1 ) P l ( x ) = 0 \frac{\mathrm{d}}{\mathrm{d} x}\left[\left(1-x^{2}\right) \frac{\mathrm{d}}{\mathrm{d} x} P_{l}(x)\right]+l(l+1)P_{l}(x)=0 dxd[(1−x2)dxdPl(x)]+l(l+1)Pl(x)=0
连带勒让德方程的解可用勒让德多项式 P l ( x ) P_l(x) Pl(x)生成
P l m = ( − 1 ) m ( 1 − x 2 ) m / 2 d m d x m P l ( x ) P_l^m = (-1)^m(1-x^2)^{m/2}\frac{d^m}{dx^m}P_l(x) Plm=(−1)m(1−x2)m/2dxmdmPl(x)
式中 ( − 1 ) m (-1)^m (−1)m叫做 S h o r t l e y − C o n d o n Shortley-Condon Shortley−Condon 相位,通常只有在量子力学中会使用这个相位,不包含这个相位同样满足微分方程
将 P l ( x ) P_l(x) Pl(x)对于 x x x的 m m m次导数,记为 P l m ( x ) P_l^m(x) Plm(x)。
P l m ( x ) = Θ = ( 1 − x 2 ) m 2 P l [ m ] ( x ) P_l^m(x) = \Theta = (1-x^2)^{\frac{m}{2}}P_l^{[m]}(x) Plm(x)=Θ=(1−x2)2mPl[m](x)
- P l ( x ) P_l(x) Pl(x)是连带勒让德函数,定义域为[-1,1]
- l , m l,m l,m分别是两带勒让德函数的阶(degree)和次(order), m ∈ ( 0 , l ) m\in (0,l) m∈(0,l)
- P l [ m ] ( x ) P_l^{[m]}(x) Pl[m](x)是对 P l m ( x ) P_l^{m}(x) Plm(x)求导。
- 广义勒让德多项式是复数,连带勒让德多项式是指实数部分。
连带勒让德多项式的前几阶表达式
1 − 1 2 P 1 1 ( x ) x − ( 1 − x 2 ) 1 2 1 24 P 2 2 ( x ) 1 6 P 2 1 ( x ) 1 2 ( 3 x 2 − 1 ) − 3 x ( 1 − x 2 ) 1 2 3 ( 1 − x 2 ) 1\\ \quad\\ -\frac{1}{2}P_1^1(x)\quad\quad x \quad\quad -(1-x^2)^{\frac{1}{2}}\\ \quad\\ \frac{1}{24}P_2^2(x)\quad\quad \frac{1}{6}P_2^1(x)\quad\quad \frac{1}{2}(3x^2-1) \quad\quad -3x(1-x^2)^{\frac{1}{2}}\quad\quad 3(1-x^2) 1−21P11(x)x−(1−x2)21241P22(x)61P21(x)21(3x2−1)−3x(1−x2)213(1−x2)
将勒让德多项式代入球谐函数
将勒让德多项式代入如下球谐函数中,即可得到球坐标系下的解 Y ( θ , φ ) Y(\theta,\varphi) Y(θ,φ)
Y ( θ , ψ ) = Θ ( θ ) Φ ( φ ) Y(\theta,\psi) = \Theta (\theta) \Phi (\varphi) Y(θ,ψ)=Θ(θ)Φ(φ)
这个解就是球谐函数
Y l m ( θ , φ ) = P l m ( c o s θ ) { s i n ( m φ ) , c o s ( m φ ) } = P l m ( c o s θ ⋅ e i m φ ) Y_l^m(\theta,\varphi) = P_l^m(cos\theta)\{sin(m\varphi),cos(m\varphi)\} = P_l^m(cos\theta \cdot e^{im\varphi}) Ylm(θ,φ)=Plm(cosθ){sin(mφ),cos(mφ)}=Plm(cosθ⋅eimφ)
利用上面的连带勒让德函数的结论,可推导出前2阶球面谐波函数的表达式。

球谐函数的性质
正交性:基函数两两正交
完备性:线性叠加可以逼近任意一个球体函数
旋转不变性:只与 θ , φ \theta,\varphi θ,φ有关,与半径无关。故球谐函数是旋转对称的。
球谐函数的使用
SH,球谐函数,归根到底只是一组基函数
有了基函数,就可以把任意一个函数,描述成几个基函数的加权和了。
例如
y ≈ 0.1 y 0 + 0.3 y 1 + 0.8 y 2 + 0.001 y 3 + . . . y \approx 0.1y_0 + 0.3y_1 + 0.8 y_2 + 0.001y_3+... y≈0.1y0+0.3y1+0.8y2+0.001y3+...
球谐基函数构成了一个函数空间(Y0,Y1,Y2,…),对于给定球面函数 f ( θ , φ ) f(\theta,\varphi) f(θ,φ),我们可以将它投影到这个空间里去,求出其在此空间中的坐标(c0,c1,c2,…),即系数。
f ( θ , φ ) f(\theta,\varphi) f(θ,φ) 在球面S上的展开式为:
f ( θ , φ ) = ∑ l = 0 ∞ ∑ m = − l l C l m Y l m ( θ , φ ) f(\theta,\varphi) = \sum_{l=0}^{\infty} \sum_{m=-l}^{l} C_l^mY_l^m(\theta,\varphi) f(θ,φ)=l=0∑∞m=−l∑lClmYlm(θ,φ)
其中 Y l m ( θ , φ ) Y_l^m(\theta,\varphi) Ylm(θ,φ) 已知,即为球谐基函数。 f ( θ , φ ) f(\theta,\varphi) f(θ,φ)为我们需要分解的函数。
需要我们计算的便是系数 C l m C_l^m Clm
根据上式变换,得到系数计算公式:
C l m = ∫ Ω f ( s ) Y l m ( s ) d s , Ω 为球面积分 C_l^m = \int_\Omega{f(s)Y_l^m(s)ds},\Omega为球面积分 Clm=∫Ωf(s)Ylm(s)ds,Ω为球面积分
也就是频域上的系数 C l m C_l^m Clm要求我们:求原函数 f f f与球谐函数 Y l m Y_l^m Ylm在球面上的乘积的积分。一般我们把这个求系数的过程叫做投影(Projection)。
在实际操作中,我们写程序时不可能会有对无穷级数进行储存和卷积的操作,一般展开项只能是有限项,也就是:
f ( s ) = ∑ l = 0 n − 1 ∑ m = − l l C l m Y l m ( s ) = ∑ i = 0 n 2 c i y i ( s ) f(s) = \sum_{l=0}^{n-1} \sum_{m=-l}^{l} C_l^mY_l^m(s) = \sum_{i=0}^{n^2}c_iy_i(s) f(s)=l=0∑n−1m=−l∑lClmYlm(s)=i=0∑n2ciyi(s)
球谐函数的实现
参照下一篇blog