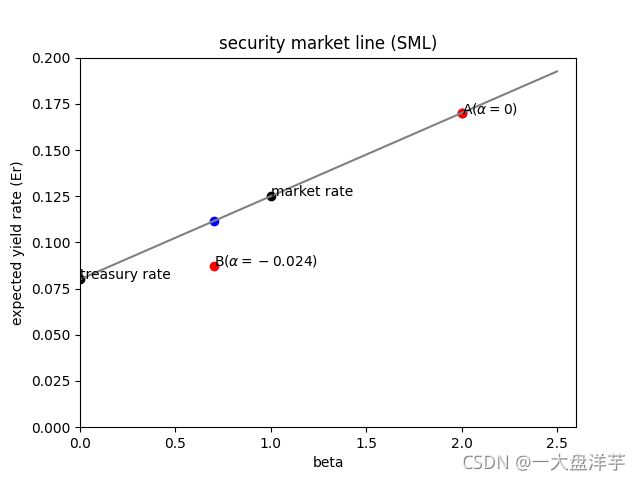
python绘制证券市场线（SML）

本文使用python绘制证券市场线（SML）。

在给定市场收益的两支股票收益率为：（国债利率为8%，市场收益可能性分别为50%）

市场收益	激进型股票A	防守型股票
5%	2%	3.5%
20%	32%	14%

1.计算两支股票的值

rM=[0.05,0.2] #市场收益率
rA=[0.02,0.32] #股票A的收益率
rB=[0.035,0.14] #股票B的收益率
betaA=round((rA[1]-rA[0])/(rM[1]-rM[0]),2) #计算股票A的beta值
betaB=round((rB[1]-rB[0])/(rM[1]-rM[0]),2) #计算股票B的beta值
print(betaA,betaB)

​可以得到​=2,=0.7

2.画图数据准备

假设国债利率为8%，市场收益可能性分别为50%。由市场期望收益率和短期国债利率可以定义证券市场函数，并计算两支股票的收益率和​值：

p=0.5
erM=p*(rM[0]+rM[1]) #计算市场期望收益率
erF=0.08 #短期国债收益率
def Er(beta): #定义SML函数
    Er=erF+beta*(erM-erF)
    return Er
ErA=Er(betaA) #计算A的均衡收益率
ErB=Er(betaB) #计算B的均衡收益率
erA=p*(rA[0]+rA[1]) #计算A的期望收益率
erB=p*(rB[0]+rB[1]) #计算B的期望收益率
alphaA=round(erA-ErA,4) #计算A的alpha值
alphaB=round(erB-ErB,4) #计算B的alpha值
print(alphaA,alphaB)

可以得到​=0,​=-0.024

3.证券市场线绘制

import matplotlib.pyplot as plt
import numpy as np
beta=np.linspace(0,2.5,26)
Er=Er(beta)
plt.plot(beta,Er,color="grey")
plt.title('security market line (SML)')
plt.ylabel('expected yield rate (Er)')
plt.xlabel('beta')
plt.ylim(0,0.2)
plt.xlim(0,2.6)
plt.scatter(0,erF,color='black')
plt.annotate('treasury rate',xy=(0,erF))
plt.scatter(1,erM,color='black')
plt.annotate('market rate',xy=(1,erM))
plt.scatter(betaA,ErA,color='blue')
plt.scatter(betaB,ErB,color='blue')
plt.scatter(betaA,erA,color='red')
plt.annotate('A'+r'($\alpha =0$)',xy=(betaA,erA))
plt.scatter(betaB,erB,color='red')
plt.annotate('B'+r'($\alpha =-0.024$)',xy=(betaB,erB))
plt.show()

完整代码：

rM=[0.05,0.2] #市场收益率
rA=[0.02,0.32] #股票A的收益率
rB=[0.035,0.14] #股票B的收益率
betaA=round((rA[1]-rA[0])/(rM[1]-rM[0]),2) #计算股票A的beta值
betaB=round((rB[1]-rB[0])/(rM[1]-rM[0]),2) #计算股票B的beta值
print(betaA,betaB)
p=0.5
erM=p*(rM[0]+rM[1]) #计算市场期望收益率
erF=0.08 #短期国债收益率
def Er(beta): #定义SML函数
    Er=erF+beta*(erM-erF)
    return Er
ErA=Er(betaA) #计算A的均衡收益率
ErB=Er(betaB) #计算B的均衡收益率
erA=p*(rA[0]+rA[1]) #计算A的期望收益率
erB=p*(rB[0]+rB[1]) #计算B的期望收益率
alphaA=round(erA-ErA,4) #计算A的alpha值
alphaB=round(erB-ErB,4) #计算B的alpha值
print(alphaA,alphaB)
import matplotlib.pyplot as plt
import numpy as np
beta=np.linspace(0,2.5,26)
Er=Er(beta)
plt.plot(beta,Er,color="grey")
plt.title('security market line (SML)')
plt.ylabel('expected yield rate (Er)')
plt.xlabel('beta')
plt.ylim(0,0.2)
plt.xlim(0,2.6)
plt.scatter(0,erF,color='black')
plt.annotate('treasury rate',xy=(0,erF))
plt.scatter(1,erM,color='black')
plt.annotate('market rate',xy=(1,erM))
plt.scatter(betaA,ErA,color='blue')
plt.scatter(betaB,ErB,color='blue')
plt.scatter(betaA,erA,color='red')
plt.annotate('A'+r'($\alpha =0$)',xy=(betaA,erA))
plt.scatter(betaB,erB,color='red')
plt.annotate('B'+r'($\alpha =-0.024$)',xy=(betaB,erB))
plt.show()