一大盘洋芋
一大盘洋芋

单因素方差分析（R）

目录

目标

原理

假设前提和模型设定

离差平方和分解

检验统计量和拒绝域

未知参数的估计

例题

应用

目标

方差分析的基本思想：通过分析不同影响来源对总体的影响程度，确定可控因素对研究对象影响力是否显著。

单因素方差分析用来研究一个控制变量的不同水平是否对观测指标变量有显著影响。

原理

观测指标变量值的变动会受控制变量和其他随机变量两方面的影响，据此，把观测指标变量的总离差平方和（SST）分解为（受控制变量影响的）组间离差平方和（SSB）和（受其他随机变量影响的）组内离差平方和（SSW）两部分，即：SST=SSB+SSW。在观测指标变量的总离差平方和中，如果组间离差平方和所占比例较大，则说明观测指标变量的变动主要由控制变量引起的，控制变量给观测指标变量有显著影响；反之，控制变量对观测指标变量没有显著影响。

假设前提和模型设定

设单因素A有r个水平，分别记为A_{1},A_{2},...A_{r}，在每个水平A_{i}(i=1,2,...,r)下的观测指标变量样本值看做一个总体，故有r个总体，基于假设前提：

1.每个总体均服从正态分布，且方差相等，即X_{i}\sim N(\mu_{i},\sigma^{2}),i=1,2,...,r

2.每个总体中抽取的样本X_{i1},X_{i2},...,X_{in_{i}},i=1,2,...,r相互独立（n_{i}为A_{i}因素水平的实验数据个数）

通过假设检验来探究期望控制变量对观测指标变量是否有显著影响，如果有，则意味着A因素不同水平对应的观测指标变量总体的均值有显著差异。可作出如下假设：

H_{0}:\mu_{1}=\mu_{2}=...=\mu_{r};

H_{1}:\mu_{1},\mu_{2},...,\mu_{r}不完全相等

方差分析的任务：

任务一：检验r个总体的均值是否相等，即完成上述假设的检验；

任务二：作出未知参数\mu_{1},\mu_{2},...,\mu_{r},\sigma^{2}的估计。

由假设前提有X_{ij}\sim N(\mu_{i},\sigma^{2})(\mu_{i},\sigma^{2}\,unknown),i=1,2,...,r;j=1,2,...,n_{i}，即有X_{ij}-\mu_{i}=\varepsilon _{ij}\sim N(0,\sigma^{2})，故X_{ij}-\mu_{i}=\varepsilon _{ij}可视为随机误差，且相互独立，由假设前提知，各个\varepsilon _{ij}相互独立。从而得到模型：

X_{ij}=\mu_{i}+\varepsilon _{ij},i=1,2,...,r;j=1,2,...,n_{i}

记数据总个数为

n=\sum_{i=1}^{r}n_{i}

总平均值为

\mu=\frac{1}{n}\sum_{i=1}^{r}n_{i}\mu_{i}

用A_{i}因素水平下的总体均值与总平均值的差异来表示 A_{i}因素水平对观测指标变量的效应：\delta_{i}=\mu_{i}-\mu。效应间的关系为

\sum^{r}_{i=1}n_{i}\delta_{i}=\sum^{r}_{i=1}n_{i}(\mu_{i}-\mu)=0

 从而改写模型为：

X_{ij}=\mu+\delta_{i}+\varepsilon _{ij},i=1,2,...,r;j=1,2,...,n_{i}

可得，前述假设等价为：

H_{0}:\delta_{1}=\delta_{2}=...=\delta_{r}=0

H_{1}:\delta_{1},\delta_{2},...,\delta_{r}不全为0

这是因为当且仅当\mu_{1}=\mu_{2}=...=\mu_{r}时，\mu_{i}=\mu，即\delta_{i}=0（i=1,2,...,r）

离差平方和分解

记 A_{i}因素水平下的样本均值为

\overline{X}_{i}=\frac{1}{n_{i}}\sum_{j=1}^{n_{i}}X_{ij}，

A因素的所有水平的样本总均值为

\overline{X}=\frac{1}{r}\sum_{i=1}^{r}\overline{X}_{i}=\frac{1}{n}\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}X_{ij}

组内离差平方和为:

SSW=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})^{2}

组间离差平方和为：

\begin{aligned} SSB&=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(\overline{X}_{i}-\overline{X})^{2}\\ &=\sum_{i=1}^{r}n_{i}(\overline{X}_{i}-\overline{X})^{2}\\ &=\sum_{i=1}^{r}n_{i}\overline{X}_{i}^{2}-n\overline{X}^{2} \end{aligned}

总离差平方和为：

\begin{aligned} SST&=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X})^{2}\\ &=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}[(X_{ij}-\overline{X}_{i})+(\overline{X}_{i}-\overline{X})]^{2}\\ &=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})^{2}+\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(\overline{X}_{i}-\overline{X})^{2}+2\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})(\overline{X}_{i}-\overline{X})\\ &=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})^{2}+\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(\overline{X}_{i}-\overline{X})^{2}\\ &=SSW+SSB \end{aligned}

SST=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X})^{2}=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}X_{ij}^{2}-n\overline{X}^{2}

检验统计量和拒绝域

由\frac{\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})^{2}}{\sigma^{2}}=\frac{(n_{i}-1)S^{2}_{i}}{\sigma^{2}}\sim\chi^{2}(n_{i}-1)和\chi^{2}分布的可加性，可得：

\frac{SSW}{\sigma^{2}}=\frac{\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(X_{ij}-\overline{X}_{i})^{2}}{\sigma^{2}}\sim\chi^{2}(\sum^{r}_{i=1}(n_{i}-1))=\chi^{2}(n-r)

因此，

E(SSW)=(n-r)\sigma^{2}

SSB可以看做r个变量\sqrt{n_{i}}(\overline{X_{i}}-\overline{X})的平方和，它们之间仅有一个线性约束条件：

\sum_{i=1}^{r}\sqrt{n_{i}}[\sqrt{n_{i}}(\overline{X}_{i}-\overline{X})]=\sum_{i=1}^{r}n_{i}(\overline{X}_{i}-\overline{X})=\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}X_{ij}-n\overline{X}=0

故知SSB的自由度是r-1。

\begin{aligned} E(SSB)&=E(\sum_{i=1}^{r}n_{i}\overline{X}_{i}^{2}-n\overline{X}^{2})\\ &=\sum_{i=1}^{r}n_{i}E(\overline{X}_{i}^{2})-nE(\overline{X}^{2})\\ &=\sum_{i=1}^{r}n_{i}[\frac{\sigma^{2}}{n_{i}}+\mu_{i}^{2}]-n(\frac{\sigma^{2}}{n}+\mu^{2})\\ &=\sum_{i=1}^{r}n_{i}[\frac{\sigma^{2}}{n_{i}}+(\mu+\delta_{i})^{2}]-n(\frac{\sigma^{2}}{n}+\mu^{2})\\ &=r\sigma^{2}+n\mu^{2}+\sum_{i=1}^{r}n_{i}\delta^{2}_{i}+2\mu\sum_{i=1}^{r}n_{i}\delta_{i}+\sigma^{2}-n\mu^{2}\\ &=(r-1)\sigma^{2}+\sum_{i=1}^{r}n_{i}\delta^{2}_{i} \end{aligned}

并且，由SSW和SSB表达式可知二者独立，所以，

当H_{0}为真时，

\frac{SSB}{\sigma^{2}}\sim\chi^{2}(r-1)

\frac{\frac{SSB}{(r-1)\sigma^{2}}}{\frac{SSW}{(n-r)\sigma^{2}}}=\frac{\frac{SSB}{(r-1)}}{\frac{SSW}{(n-r)}}\sim F(r-1,n-r)

当 H_{0}不为真时，

E(SSB)=(r-1)\sigma^{2}+\sum_{i=1}^{r}n_{i}\delta^{2}_{i}>(r-1)\sigma^{2}

\frac{\frac{SSB}{(r-1)}}{\frac{SSW}{(n-r)}}\geqslant k

因此可得拒绝域为：

F=\frac{\frac{SSB}{(r-1)}}{\frac{SSW}{(n-r)}}\geqslant F_{\alpha}(r-1,n-r)

因SST的n个变量X_{ij}-\overline{X}之间有一个约束条件\overline{X}=\frac{1}{r}\sum_{i=1}^{r}\overline{X}_{i}=\frac{1}{n}\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}X_{ij}，所以SSW的自由度为n-1。

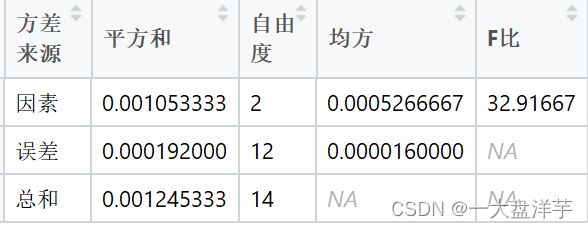
据上述分析结果，可得方差分析表：

单因素试验方差分析表
方差来源 平方和 自由度 均方 F比
因素A SSB r-1 \overline{SSB}=\frac{SSB}{r-1} F=\frac{\overline{SSB}}{\overline{SSW}}
误差 SSW n-r \overline{SSW}=\frac{SSW}{n-r}
总和 SST n-1

在实际中，可先计算SST和SSB，再由二者相减得到SSW，以简便计算。

未知参数的估计

由E(\overline{X})=\mu知，\mu的无偏估计为：\hat{\mu}=\overline{X}

由E(\overline{X}_{i})=\mu_{i}知，\mu_{i}的无偏估计为：\hat{\mu}_{i}=\overline{X}_{i}

不管H_{0}是否为真，E(\frac{SSW}{n-r})=\sigma^{2}，可知\sigma^{2}的无偏估计为：\hat{\sigma^{2}}=\frac{SSW}{n-r}

当拒绝H_{0}时，效应\delta_{1},\delta_{2},...,\delta_{r}不全为0，且E(\delta_{i})=E(\mu_{i}-\mu)，可知，\delta_{i}的无偏估计为\hat{\delta}_{i}=\hat{\mu}_{i}-\hat{\mu}=\overline{X}_{i}-\overline{X}

 当拒绝H_{0}时，常常需要作出两总体N(\mu_{j},\sigma^{2})和N(\mu_{k},\sigma^{2})，j\neq k的均值差\mu_{j}-\mu_{k}=\delta_{j}-\delta_{k}的区间估计，由于

E(\overline{X}_{j}-\overline{X}_{k})=\mu_{j}-\mu_{k}

D(\overline{X}_{j}-\overline{X}_{k})=\sigma^{2}(\frac{1}{n_{j}}+\frac{1}{n_{k}})

并且\overline{X}_{j}-\overline{X}_{k}与\hat{\sigma^{2}}=\frac{SSW}{n-r}独立，于是，

\frac{(\overline{X}_{j}-\overline{X}_{k})-(\mu_{j}-\mu_{k})}{\sqrt{\frac{SSW}{n-r}(\frac{1}{n_{j}}+\frac{1}{n_{k}})}}\\ =\frac{\frac{(\overline{X}_{j}-\overline{X}_{k})-(\mu_{j}-\mu_{k})}{\sigma\sqrt{\frac{1}{n_{j}}+\frac{1}{n_{k}}}}}{\sqrt{\frac{SSW}{\sigma^{2}(n-r)}}}\sim t(n-r)

据此得均值差\mu_{j}-\mu_{k}=\delta_{j}-\delta_{k}的置信水平为1-\alpha的置信区间为：

((\overline{X}_{j}-\overline{X}_{k})\pm t_{\alpha/2}(n-r)\sqrt{\frac{SSW}{n-r}(\frac{1}{n_{j}}+\frac{1}{n_{k}})})

例题

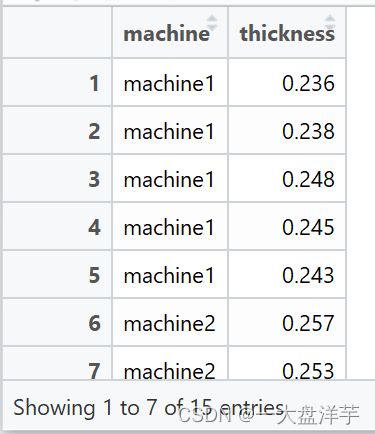
设有三台机器，用来生产规格相同的铝合金薄板，并且假定除了机器这一因素之外，其他条件都相同。取样并测量薄板的厚度精确到千分之一厘米，得到结果（服从单因素方差分析假设前提）：

machine1=c(0.236,0.238,0.248,0.245,0.243)
machine2=c(0.257,0.253,0.255,0.254,0.261)
machine3=c(0.258,0.264,0.259,0.267,0.262)
data1=cbind(machine1,machine2,machine3)
write.csv(data1,"D:/CSDN/方差分析/r/data1.csv",row.names = FALSE)

单因素方差分析（R）_第1张图片

先假设检验三个总体的均值是否相等 

做出假设：

H_{0}:\mu_{1}=\mu{2}=\mu{3}

H_{1}:\mu_{1},\mu_{2},\mu_{3}不全相等

由数据可知，r=3，n_{1}=n_{2}=n_{3}=5，n=15，则，

SST=\sum_{i=1}^{3}\sum_{j=1}^{n_{i}}X_{ij}^{2}-\frac{(\sum_{i=1}^{3}\sum_{j=1}^{n_{i}}X_{ij})^{2}}{15}

SSB=\sum_{i=1}^{3}\frac{(\sum_{j=1}^{n_{i}}X_{ij})^{2}}{n_{i}}-\frac{(\sum_{i=1}^{3}\sum_{j=1}^{n_{i}}X_{ij})^{2}}{n}

SSW=SST-SSB

单因素方差分析（R）_第2张图片

F比=32.91667>F_{0.05}(2,12)=3.885294

故在0.05显著性水平下拒绝H_{0}，认为各台机器生产的薄板厚度有显著的差异。

write.csv(data1,"D:/CSDN/方差分析/r/data1.csv",row.names = FALSE)
Data1=read.csv("D:/CSDN/方差分析/r/data1.csv")
n=15
r=3
n1=n2=n3=5
SST=sum(c(Data1$machine1**2,
          Data1$machine2**2,
          Data1$machine3**2))-(sum(Data1)**2)/n
SSB=sum(c((sum(Data1$machine1)**2)/n1,
          (sum(Data1$machine2)**2)/n2,
            (sum(Data1$machine3)**2)/n3))-(sum(Data1)**2)/n
SSW=SST-SSB
tab1=data.frame(matrix(nrow = 3,ncol = 5))
colnames(tab1)=c("方差来源","平方和","自由度","均方","F比")
tab1[1,1]="因素"
tab1[2,1]="误差"
tab1[3,1]="总和"
tab1[1,2]=SSB
tab1[2,2]=SSW
tab1[3,2]=SST
tab1[1,3]=r-1
tab1[2,3]=n-r
tab1[3,3]=n-1
tab1[1,4]=SSB/(r-1)
tab1[2,4]=SSW/(n-r)
tab1[1,5]=tab1[1,4]/tab1[2,4]
qf(1-0.05,r-1,n-r)

接着对未知参数\sigma^{2},\mu_{i},\delta_{i}(i=1,2,3)进行点估计及均值差的0.95置信区间

\hat{\sigma^{2}}=\frac{SSW}{n-r}

1.6e-05

\hat{\mu}=\overline{X}

0.2533333

\hat{\mu}_{i}=\overline{X}_{i}

\hat{\delta}_{i}=\hat{\mu}_{i}-\hat{\mu}=\overline{X}_{i}-\overline{X}

((\overline{X}_{j}-\overline{X}_{k})\pm t_{\alpha/2}(n-r)\sqrt{\frac{SSW}{n-r}(\frac{1}{n_{j}}+\frac{1}{n_{k}})})

单因素方差分析（R）_第3张图片

 单因素方差分析（R）_第4张图片

hatsigma2=SSW/(n-r)
hatmu=mean(c(mean(Data1$machine1),
             mean(Data1$machine2),
             mean(Data1$machine3)))
tab2=data.frame(matrix(nrow = 2,ncol = 3))
colnames(tab2)=c("machine1","machine2","machine3")
rownames(tab2)=c("hatmu","hatdelta")
tab2[1,1]=mean(Data1$machine1)
tab2[1,2]=mean(Data1$machine2)
tab2[1,3]=mean(Data1$machine3)
tab2[2,1]=tab2[1,1]-hatmu
tab2[2,2]=tab2[1,2]-hatmu
tab2[2,3]=tab2[1,3]-hatmu
tab3=data.frame(matrix(nrow = 3,ncol = 2))
colnames(tab3)=c("lower","upper")
rownames(tab3)=c("interval12","interval13","interval23")
t=qt(1-0.025,n-r)
tab3[1,1]=mean(Data1$machine1)-mean(Data1$machine2)-
  t*sqrt(SSW/(n-r)*(1/n1+1/n2))
tab3[1,2]=mean(Data1$machine1)-mean(Data1$machine2)+
  t*sqrt(SSW/(n-r)*(1/n1+1/n2))
tab3[2,1]=mean(Data1$machine1)-mean(Data1$machine3)-
  t*sqrt(SSW/(n-r)*(1/n1+1/n3))
tab3[2,2]=mean(Data1$machine1)-mean(Data1$machine3)+
  t*sqrt(SSW/(n-r)*(1/n1+1/n3))
tab3[3,1]=mean(Data1$machine2)-mean(Data1$machine3)-
  t*sqrt(SSW/(n-r)*(1/n2+1/n3))
tab3[3,2]=mean(Data1$machine2)-mean(Data1$machine3)+
  t*sqrt(SSW/(n-r)*(1/n2+1/n3))

应用

library(reshape2)
tData1=melt(Data1,
            measure.vars=c("machine1","machine2","machine3"),
            variable.name = "machine",
            value.name = "thickness")

单因素方差分析（R）_第5张图片

aov=aov(thickness~machine,data=tData1)
summary(aov)

单因素方差分析（R）_第6张图片

你可能感兴趣的:(概率论)

  • 如何有效的学习AI大模型？ Python程序员罗宾 学习人工智能语言模型自然语言处理架构
    学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
  • 日记2021-3-8 思考z
    今天开课第一天，对于今天的目标完成的还不错早上起床赖了一下，下午去图书馆呆了2个多小时，晚自习看了概率论与统计学，单词：talent天赋，才能，thick厚的，obstacleto对……障碍，introduce介绍，传入，thin瘦的，稀薄的，thorough彻底的，完全的，occurredto想到，invent发明，throat喉咙，ofcourse当然，thunder雷，雷声，tide潮汐，o
  • PDF和CDF 薛定谔的猫_大雪 概率论
    在概率论和统计学中，PDF和CDF是两种描述随机变量分布的重要函数：ProbabilityDensityFunction(PDF)：概率密度函数是用来描述连续随机变量可能取值的概率分布的函数。对于一个连续型随机变量X，其PDFf(x)定义为在某个取值x处的概率密度，即X在该值附近出现的概率密度。PDF的积分可以得到概率，即在某个区间内随机变量出现的概率。CumulativeDensityFunct
  • Python 数学建模——方差分析 Desire.984 Python数学建模数学建模python概率论
    文章目录前言单因素方差分析原理核心代码双因素方差分析数学模型分析依据典型代码前言  方差分析也是概率论中非常重要的内容，有时数学建模需要用到。方差分析是干什么的？如果说假设检验用于分析两个总体之间的均值μ1,μ2\mu_1,\mu_2μ1,μ2是否存在显著的差别，那么方差分析就是分析两个以上总体之间的均值是否存在显著的差别。单因素方差分析用途：已知一个量AAA可能会影响XXX，AAA的不同取值可能
  • 数据分析面试【概率论与统计学】总结之-----统计学常见面试题整理 天阑的芋头 #数据分析—统计学知识数据分析统计学数据分析面试
    阅读之前看这里：博主是正在学习数据分析的一员，博客记录的是在学习过程中一些总结，也希望和大家一起进步，在记录之时，未免存在很多疏漏和不全，如有问题，还请私聊博主指正。博客地址：天阑之蓝的博客，学习过程中不免有困难和迷茫，希望大家都能在这学习的过程中肯定自己，超越自己，最终创造自己。目录1.用简洁的话语阐述随机变量的含义2.划分连续型随机变量和离散型随机变量的依据3.常见的分布函数/概率密度函数，以
  • 感悟文是很容易写的 林天歌
    生活感悟是很容易写的，只要你生活中稍稍关注一下周围在发生什么，随便什么事情都可以，甚至编一件事都可以，然后为之赋予一个意义。举例子的话，比如说我可以写我的概率论老师，每节课三小时，两小时都是在讲课堂无关的事情，都是在讲一些她以为的人生道理，却不知道因为她讲得太多，加上她使用互联网的能力不足，她讲得已经完全不能触动到学生的神经，反倒还促进了一些学生的逃课。这就是典型的以己度人，她以为她在分享自己认为
  • 深度学习算法，该如何深入，举例说明 liyy614 深度学习
    深度学习算法的深入学习可以从理论和实践两个方面进行。理论上，深入理解深度学习需要掌握数学基础（如线性代数、概率论、微积分）、机器学习基础和深度学习框架原理。实践上，可以通过实现和优化深度学习模型来提升技能。理论深入数学基础线性代数：理解向量、矩阵、特征值和特征向量等，对于理解神经网络的权重和偏置矩阵至关重要。概率论：用于理解模型的不确定性，如Dropout等正则化技术。微积分：理解梯度下降等优化算
  • 机械学习—零基础学习日志（概率论总笔记5） 学长小陈来帮你 学习笔记概率论算法深度学习机器学习
    引言——“黑天鹅”要获得95%以上置信度的统计结果，需要被统计的对象出现上千次，但是如果整个样本只有几千字，被统计的对象能出现几次就不错了。这样得到的数据可能和真实的概率相差很远。怎么避免“黑天鹅”？古德-图灵折扣估计法在词语统计中，有点词语虽然是出现0次，但是实际的出现概率并不是永远不可能的零。那需要把一些概率转移给到这些词语。古德的做法实际上就是把出现1次的单词的总量，给了出现0次的，出现2次
  • Python 数学建模——假设检验 Desire.984 Python数学建模python数学建模概率论
    文章目录前言参数假设检验单个总体均值的假设检验σ\sigmaσ已知σ\sigmaσ未知两个总体均值的假设检验参考代码非参数假设检验分布拟合检验——卡方检验KS检验（Kolmogorov-Smirnov检验）Wilcoxon检验Wilcoxon符号秩检验Wilcoxon秩和检验前言  假设检验是概率论中相当重要的内容。一般是先提出一个原假设H0H_0H0和一个对立的备择假设H1H_1H1，通过数学方
  • 非理工科院校怎么打好数学建模比赛 | 南川笔记 南川笔记
    Proposition1非理工科院校最好不要打数学建模比赛。虽说“一次建模，终身受益”，但毕竟数学建模既要数学理论的支撑（不仅仅是大学里的微积分、线性代数和概率论与统计，更多的是基于微积分的常偏微分方程、基于线性代数的运筹学和基于概率论与统计的统计分析内容），还要编程的支撑（不是常规的C语言或者Java程序，也不是这几年很火的Python编程，而是基于数值运算的Matlab和基于统计的R），这在一
  • Python的图形化界面编程 iteye_20668 Pythonpython
    2017.2.14好久没有写代码了，感觉过一个年弄的什么也没有干成，好像看了下c++,突然发现现在来看C++,要简单了好多，并且指针也没有那么难了，然后就是看了下机器学习，感觉有点小难，现在发现好多都涉及到高数，概率论和线性代数的知识，想想当初把这些学的是一塌糊涂。然后上次和胡杨大大聊天的时候，他说好多东西都是在实践中去学习的。好了，继续我的Python吧，Python的图形化界面编程。impor
  • python机器学习算法--贝叶斯算法 在下小天n 机器学习python机器学习算法
    1.贝叶斯定理在20世纪60年代初就引入到文字信息检索中，仍然是文字分类的一种热门（基准）方法。文字分类是以词频为特征判断文件所属类型或其他（如垃圾邮件、合法性、新闻分类等）的问题。原理牵涉到概率论的问题，不在详细说明。sklearn.naive_bayes.GaussianNB(priors=None,var_smoothing=1e-09)#Bayes函数·priors：矩阵，shape=[n
  • 【概率论】理解贝叶斯（Bayes）公式：为什么疾病检测呈阳性，得这种病的概率却不高？ seh_sjlj 概率论概率论学习数学经验分享
    先说结论：因为假阳性的人数相比于真阳性太多了。具体是怎么回事呢？咱们慢慢分析。文章目录一、贝叶斯公式二、典例分析三、贝叶斯公式的本质思考（摘自教材）一、贝叶斯公式定理1（贝叶斯公式）设有事件A,BA,BA,B，P(A)>0P(A)>0P(A)>0，P(B)>0P(B)>0P(B)>0，则P(B∣A)=P(B)P(A∣B)P(A)P(B|A)=\frac{P(B)P(A|B)}{P(A)}P(B∣A
  • 愚者才悲观｜每日复盘D32 _李子昂
    我是李子昂，一个热爱生活、积极向上的“人生梦想家”。爱阅读、记录生活，这是我的第三十二天复盘❤2019.12.1232/3651.感恩创造的不可思议的今天早起一件事：打卡✔（每天比昨天早起两分钟）早读任务：第一课，课文两段✔马原第一章大题背诵✘古诗词一首✘三只青蛙:阅读一小时✔概率论前三章✘图片发自App2.今日小确幸感恩YCX送我的奶茶，紫薯和冬天很配❤感恩早上的挣扎顺利的早起了两分钟，明天加油
  • 【晨间日记】 2020年9月23日 语瞳SAMA
    2020年9月23日天气：小雨【90天践行目标】（108/120）①5：30早起②22：30早睡③写晨间日记【昨日践行】①5：41起床②22：29入睡③晨间日记已达成【今日青蛙】①完成概率论和离散数学作业②午间冥想③洗衣服*昨日三只青蛙已达成【反思日志】①早晨听这门Java课，真的有种“虽然是使用中文教学，但是上起来却和外语课一样”的感觉，好多未知的术语糅杂在一起，整堂课听着就跟猜谜似的，太离谱了
  • 2.1概率统计的世界 极客探索者 量化交易概率论
    欢迎来到概率统计的世界！在量化交易中，概率统计是至关重要的工具。通过理解概率，我们可以用数学的方法来描述市场行为，预测未来走势，并制定交易策略。让我们一起从基础概念开始，逐步深入，揭开概率统计的神秘面纱。1.1概率论的基本概念与应用概率是用来描述某个事件发生可能性的数值。例如，丢一枚硬币，正面朝上的概率是50%。这个概率可以用数学公式表示为：在量化交易中，我们常常需要计算各种事件的概率，例如股票价
  • Matlab实现多传感器信息融合（D-S证据推论） 冬天都会过去
    D-S证据理论是对贝叶斯推理方法推广，主要是利用概率论中贝叶斯条件概率来进行的，贝叶斯条件概率需要知道先验概率。而D-S证据理论不需要知道先验概率，能够很好地表示“不确定”，被广泛用来处理不确定数据。（对来自多传感器数据的融合处理）适用于：信息融合、专家系统、情报分析、法律案件分析、多属性决策分析1、D-S证据理论知识介绍（1）四大定义基本概率分配、信任函数、似然函数、信任区间其中，函数m为识别框
  • 概率论中的卷积公式 Ctrl+CV九段手 概率论卷积公式卷积神经网络概率论概率论与数理统计笔记经验分享
    目录简介卷积公式的推导与应用实际例子卷积公式在多维情况下的推导和应用是什么？多维卷积的推导多维卷积的应用延伸拓展如何使用卷积公式解决实际问题，例如信号处理中的噪声消除？在统计学中，卷积公式是如何应用于样本量估计和假设检验的？卷积公式在量子力学中的应用有哪些例子？如何证明卷积公式对于独立随机变量之和的概率密度函数的重要性？简介在概率论中，卷积公式是用于计算两个独立随机变量之和的概率密度函数的重要工具
  • 亦菲喊你来学机器学习（14） --贝叶斯算法 方世恩 机器学习算法人工智能pythonscikit-learn
    文章目录贝叶斯一、贝叶斯定理二、贝叶斯算法的核心概念三、贝叶斯算法的优点与局限优点：局限：四、构建模型训练模型测试模型总结贝叶斯贝叶斯算法（Bayesianalgorithm）是一种基于贝叶斯定理的机器学习方法，主要用于估计模型参数和进行概率推断。以下是对贝叶斯算法的详细解析：一、贝叶斯定理贝叶斯定理是概率论中的一个基本定理，它描述了条件概率之间的关系。该定理的数学表达式为：P(A∣B)=P(B)
  • AI大模型副业变现之路，有技术就有收入！ AI大模型-王哥 人工智能AI大模型大模型大模型学习大模型教程大模型入门
    在当今时代，AI大模型的应用越来越广泛，利用这些技术开展副业赚钱已成为可能。以下是一份详细的指南，帮助你了解需要学习的内容以及如何操作。一、需要学习的内容基础知识储备（1）数学知识：线性代数、概率论与数理统计、微积分等，这些是理解AI算法的基础。（2）编程技能：掌握Python编程语言，因为Python在AI领域有丰富的库和框架支持。（3）机器学习原理：了解常见的机器学习算法，如线性回归、决策树、
  • 小琳 AI 课堂：机器学习 小琳ai 小琳AI课堂人工智能机器学习
    嘿，朋友们！欢迎来到小琳AI课堂机器学习：如同让计算机拥有超能力的神奇魔法机器学习，这门超酷的多领域交叉学科，居然融合了概率论、统计学、逼近论、凸分析、算法复杂度理论等等好多学科。它的关键就在于让计算机凭借数据和算法去学习，然后像个小超人似的，拥有预测和决策的超强能力！从技术实现的层面来讲，主要分成监督学习、无监督学习和强化学习这三大类别监督学习：在有标记的数据集上展开学习。打个比方哈，根据已知的
  • 计算机保研/考研面试题——数学篇 安晴晚风 计算机保研/考研专业课面试考研面试
    笔者在2023年参加了部分985和华五计算机夏令营和预推免面试，遇到了不少数学问题，以下是笔者的一些总结，从高数、线代、概率论三个方面讨论。（对保研er和考研er均适用，如需要其他学科的问题请关注我~）相关文章：计算机保研/考研面试题——数据结构与算法篇-CSDN博客计算机保研/考研面试题——操作系统篇-CSDN博客计算机保研/考研面试题——计算机网络篇-CSDN博客计算机保研/考研面试题——编程
  • 中心极限定理 不倒的不倒翁先森 概率论
    中心极限定理（CentralLimitTheorem，CLT）是概率论中的一个重要定理，它说明了在某些条件下，独立随机变量的和（或平均值）趋向于正态分布的性质。具体来说，中心极限定理可以描述为：定理表述：设(X1,X2,…,Xn)(X_1,X_2,\dots,X_n)(X1,X2,…,Xn)是一组相互独立、服从相同分布的随机变量，其数学期望为μ\muμ，方差为σ2\sigma^2σ2（有限且不为零
  • 2019-03-20记录及学习计划更正 逆风飞翔的鸟
    今天早晨早早的就坐上了返回学校的高铁，自己复习的进度稍慢了一些，不过没关系，这几天再追回来，最近发现虽然自己数学的做题能力有所提升，但是熟练程度还差很多，所以接下来高等数学要多做题，线性代数基础已经复习完毕，不能丢下，每天要做一定量的练习来保持住自己的水平。概率论与数理统计自己感觉有些困难，需要从课本开始认真的复习。关于英语我已经用百词斩背了有400左右的单词了，但是不是很扎实，所以自己要提升自己
  • 深度学习如何入门？ 科学的N次方 深度学习
    入门深度学习需要系统性的学习和实践经验积累，以下是一份详细的入门指南，包含了关键的学习步骤和资源：预备知识：•编程基础：熟悉Python编程语言，它是深度学习领域最常用的编程语言。确保掌握变量、条件语句、循环、函数等基本概念，并学习如何使用Python处理数据和文件操作。•数学基础：理解线性代数（矩阵运算、向量空间等）、微积分（导数、梯度求解等）、概率论与统计学（期望、方差、概率分布、最大似然估计
  • 2022-05-14 败者食尘_40a0
    本文结构速览：一、SQL题二、机器学习&概率论三、开放性问题01SQL题面试真题：现有一张用户签到表（user_sign_d）,标记用户每日是否签到，表结构如下sign_date:日期user_id:用户IDif_sign:当日是否签到,1表示签到，0表示未签到问题①：请计算截止到当前每个用户已经连续签到的天数（输出表仅包含当天签到的所有用户，计算其连续签到的天数）输出表结构如下：user_id:
  • 深度学习如何入门？ nanshaws yolov5深度学习
    深度学习是机器学习的一个子领域，它基于人工神经网络的研究。入门深度学习可以分为以下几个步骤：基础知识准备：（1）掌握基础数学知识，特别是线性代数、概率论和统计学、微积分。（2）学习编程语言，Python是目前最流行的深度学习语言，因其简洁易学且有大量的库支持。（3）了解机器学习基础，包括监督学习和非监督学习的概念、模型评估与选择等。学习深度学习理论：（1）理解神经网络的基本组成，如神经元、激活函数
  • 【个人学习笔记】概率论与数理统计知识梳理【五】 已经是全速前进了 概率论
    文章目录第五章、大数定律及中心极限定理一、大数定律1.1基本概念1.2弱大数定理二、中心极限定理独立同分布的中心极限定理定理总结第五章、大数定律及中心极限定理写博客比想象中费劲得多，公式得敲好久，所以只得随缘更更了，想写一些机器学习相关的东西，但是强迫症又不允许我把这个扔掉不管，我太难了Orz这一节的内容比较深，即使我是一个喜欢数学的工科生，也没有精力再去深究了，各式各样的大数定律及中心极限定理我
  • 机器学习笔记 rl染离 机器学习笔记人工智能
    什么是机器学习：机器学习是一门多学科交叉专业，涵盖概率论知识，统计学知识，近似理论知识和复杂算法知识，使用计算机作为工具并致力于真实实时的模拟人类学习方式，并将现有内容进行知识结构划分来有效提高学习效率。机器学习有下面几种定义：（1）机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能。（2）机器学习是对能通过经验自动改进的计算机算法的研究。（3）
  • 机器学习是什么 MarkHD 机器学习
    机器学习是一门跨学科的学科，它使用计算机模拟或实现人类学习行为，通过不断地获取新的知识和技能，重新组织已有的知识结构，从而提高自身的性能。机器学习涉及多个学科，如概率论、统计学、逼近论、凸分析、算法复杂度理论等。机器学习的主要任务是指导计算机从数据中学习，然后利用经验来改善自身的性能，不需要进行明确的编程。机器学习算法会不断进行训练，从大型数据集中发现模式和相关性，然后利用这些模式来预测新数据的结
  • 二分查找排序算法 周凡杨 java二分查找排序算法折半
    一：概念 二分查找又称 折半查找（ 折半搜索/ 二分搜索），优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而 查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表 分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步
  • java中的BigDecimal bijian1013 javaBigDecimal
            在项目开发过程中出现精度丢失问题，查资料用BigDecimal解决，并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习，特转载。         原文地址：http://blog.csdn.net/ugg/article/de
  • Shell echo命令详解 daizj echoshell
    Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似，都是用于字符串的输出。命令格式： echo string 您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串: echo "It is a test" 这里的双引号完全可以省略，以下命令与上面实例效果一致： echo Itis a test 2.显示转义
  • Oracle DBA 简单操作 周凡杨 oracle dba sql
    --执行次数多的SQL select sql_text,executions from (      select sql_text,executions from v$sqlarea order by executions desc      ) where rownum<81;  &nb
  • 画图重绘 朱辉辉33 游戏
      我第一次接触重绘是编写五子棋小游戏的时候，因为游戏里的棋盘是用线绘制的，而这些东西并不在系统自带的重绘里，所以在移动窗体时，棋盘并不会重绘出来。所以我们要重写系统的重绘方法。   在重写系统重绘方法时，我们要注意一定要调用父类的重绘方法，即加上super.paint(g)，因为如果不调用父类的重绘方式，重写后会把父类的重绘覆盖掉，而父类的重绘方法是绘制画布，这样就导致我们
  • 线程之初体验 西蜀石兰 线程
    一直觉得多线程是学Java的一个分水岭，懂多线程才算入门。 之前看《编程思想》的多线程章节，看的云里雾里，知道线程类有哪几个方法，却依旧不知道线程到底是什么？书上都写线程是进程的模块，共享线程的资源，可是这跟多线程编程有毛线的关系，呜呜。。。 线程其实也是用户自定义的任务，不要过多的强调线程的属性，而忽略了线程最基本的属性。 你可以在线程类的run()方法中定义自己的任务，就跟正常的Ja
  • linux集群互相免登陆配置 林鹤霄 linux
    配置ssh免登陆 1、生成秘钥和公钥    ssh-keygen -t rsa 2、提示让你输入，什么都不输，三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub    其中id_rsa为秘钥，id_rsa.pub为公钥，使用公钥加密的数据只有私钥才能对这些数据解密    c
  • mysql : Lock wait timeout exceeded; try restarting transaction aigo mysql
    原文：http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html   原因是你使用的InnoDB   表类型的时候, 默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s, 因为有的锁等待超过了这个时间,所以抱错.   你可以把这个时间加长,或者优化存储
  • Socket编程 基本的聊天实现。 alleni123 socket
    public class Server { //用来存储所有连接上来的客户 private List<ServerThread> clients; public static void main(String[] args) { Server s = new Server(); s.startServer(9988); } publi
  • 多线程监听器事件模式(一个简单的例子) 百合不是茶 线程监听模式
        多线程的事件监听器模式   监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到        创建多线程的事件监听器模式 思路:    1, 创建线程并启动,在创建线程的位置设置一个标记     2,创建队
  • spring InitializingBean接口 bijian1013 javaspring
    spring的事务的TransactionTemplate，其源码如下： public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{ ... } TransactionTemplate继承了DefaultT
  • Oracle中询表的权限被授予给了哪些用户 bijian1013 oracle数据库权限
            Oracle查询表将权限赋给了哪些用户的SQL，以备查用。 select t.table_name as "表名", t.grantee as "被授权的属组", t.owner as "对象所在的属组"
  • 【Struts2五】Struts2 参数传值 bit1129 struts2
    Struts2中参数传值的3种情况 1.请求参数绑定到Action的实例字段上 2.Action将值传递到转发的视图上 3.Action将值传递到重定向的视图上   一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上 Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上，绑定的规则使用ognl表达式语言
  • 【Kafka十四】关于auto.offset.reset[Q/A] bit1129 kafka
    I got serveral questions about  auto.offset.reset. This configuration parameter governs how  consumer read the message from  Kafka when  there is no initial offset in ZooKeeper or
  • nginx gzip压缩配置 ronin47 nginx gzip 压缩范例
    nginx gzip压缩配置 更多 0 nginx gzip 配置   随着nginx的发展，越来越多的网站使用nginx，因此nginx的优化变得越来越重要，今天我们来看看nginx的gzip压缩到底是怎么压缩的呢？ gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小，这样，用
  • java-13.输入一个单向链表，输出该链表中倒数第 k 个节点 bylijinnan java
    two cursors. Make the first cursor go K steps first. /* * 第 13 题：题目：输入一个单向链表，输出该链表中倒数第 k 个节点 */ public void displayKthItemsBackWard(ListNode head,int k){ ListNode p1=head,p2=head;
  • Spring源码学习-JdbcTemplate queryForObject bylijinnan javaspring
    JdbcTemplate中有两个可能会混淆的queryForObject方法： 1. Object queryForObject(String sql, Object[] args, Class requiredType) 2. Object queryForObject(String sql, Object[] args, RowMapper rowMapper) 第1个方法是只查
  • [冰川时代]在冰川时代,我们需要什么样的技术? comsci 技术
         看美国那边的气候情况....我有个感觉...是不是要进入小冰期了?      那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段...   &nb
  • js 获取浏览器型号 cuityang js浏览器
    根据浏览器获取iphone和apk的下载地址 <!DOCTYPE html> <html> <head>     <meta charset="utf-8" content="text/html"/>     <meta name=
  • C# socks5详解 转 dalan_123 socketC#
    http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html  这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯，Socket4的实现是类似的，注意的事，这里不是讲用C#实现一个代理服务器，因为实现一个代理服务器需要实现很多协议，头大，而且现在市面上有很多现成的代理服务器用，性能又好，
  • 运维 Centos问题汇总 dcj3sjt126com 云主机
    一、sh 脚本不执行的原因 sh脚本不执行的原因 只有2个 1.权限不够 2.sh脚本里路径没写完整。   二、解决You have new mail in /var/spool/mail/root 修改/usr/share/logwatch/default.conf/logwatch.conf配置文件 MailTo = MailFrom   三、查询连接数
  • Yii防注入攻击笔记 dcj3sjt126com sqlWEB安全yii
    网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查，可以使用正则表达式或者直接输入字符判断，大部分是只允许输入字母和数字的，其它字符度不允许；对于内容复杂表单的内容，应该对html和script的符号进行转义替换：尤其是<,>,',"",&这几个符号 这里有个转义对照表： http://blog.csdn.net/xinzhu1990/articl
  • MongoDB简介[一] eksliang mongodbMongoDB简介
    MongoDB简介 转载请出自出处：http://eksliang.iteye.com/blog/2173288 1.1易于使用        MongoDB是一个面向文档的数据库，而不是关系型数据库。与关系型数据库相比，面向文档的数据库不再有行的概念，取而代之的是更为灵活的“文档”模型。        另外，不
  • zookeeper windows 入门安装和测试 greemranqq zookeeper安装分布式
    一、序言       以下是我对zookeeper 的一些理解：      zookeeper 作为一个服务注册信息存储的管理工具，好吧，这样说得很抽象，我们举个“栗子”。       栗子1号：       假设我是一家KTV的老板，我同时拥有5家KTV，我肯定得时刻监视
  • Spring之使用事务缘由(2-注解实现) ihuning spring
      Spring事务注解实现   1. 依赖包：     1.1 spring包：           spring-beans-4.0.0.RELEASE.jar           spring-context-4.0.0.
  • iOS App Launch Option 啸笑天 option
    iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:，其中第二个参数launchOptions为NSDictionary类型的对象，里面存储有此程序启动的原因。   launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节 。 1、若用户直接
  • jdk与jre的区别（_） macroli javajvmjdk
    简单的说JDK是面向开发人员使用的SDK，它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包，可以包括函数库、编译程序等。  JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境，是面向Java程序的使用者，而不是开发者。 如果安装了JDK，会发同你
  • Updates were rejected because the tip of your current branch is behind qiaolevip 学习永无止境每天进步一点点众观千象git
    $ git push joe prod-2295-1 To [email protected]:joe.le/dr-frontend.git ! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward) error: failed to push some refs to '[email protected]
  • [一起学Hive]之十四-Hive的元数据表结构详解 superlxw1234 hivehive元数据结构
    关键字：Hive元数据、Hive元数据表结构   之前在 “[一起学Hive]之一–Hive概述，Hive是什么”中介绍过，Hive自己维护了一套元数据，用户通过HQL查询时候，Hive首先需要结合元数据，将HQL翻译成MapReduce去执行。 本文介绍一下Hive元数据中重要的一些表结构及用途，以Hive0.13为例。   文章最后面，会以一个示例来全面了解一下，
  • Spring 3.2.14，4.1.7，4.2.RC2发布 wiselyman Spring 3
      Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。   其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止)，后续会继续根据需求和bug发布维护版本。此时，Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。   其中Spring 4.1.7主要包含这些更新内容。
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他