监督学习概述
监督学习的特点是既有输入,也有结果。
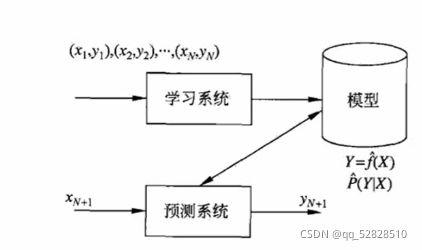
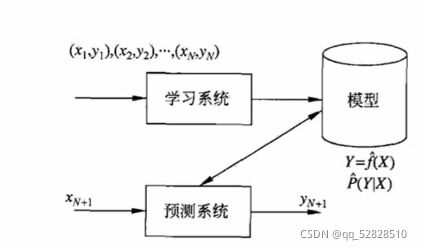
我们输入的数据是(x,y)这种样本点的模式,x是我们输入的数据量,y是我们想要的结果。通过学习系统得到一个模型,得到一个y和x的函数关系,或者一个条件概率模型,即y在x的前提下发生的概率。
监督学习(Supervised Learning)算法构建了包括输入和所需输出的一组数据的数学模型。这些数据称为训练数据,由一组训练样本组合。
监督学习主要包括分类和回归。当输出被限制为有限的一组值(离散数值)时使用分类算法;当输出可以具有范围内的任何数值(连续数值)时使用回归算法。
相似度学习是和回归和分类都密切相关的一类监督机器学习,它的目标是使用相似性函数从样本中学习,这个函数可以度量两个对象之间的相似度或者关联度。它在排名、推荐系统、视觉识别跟踪、人脸识别等方面有着很好的应用场景。
1.监督学习应用举例
1.1 预测房价或房屋出售情况
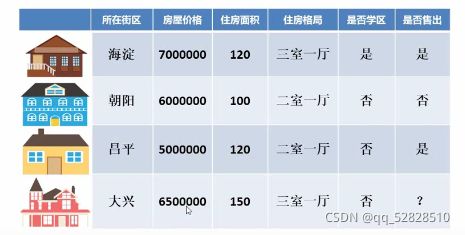
我们将所在街区、房屋价格、住房面积、住房格局、是否学区总体当成一个x,是否售出当做一个y输入模型内,再通过模型预测第四套房子是否售出。由于结果只有“是”和“否”这两个答案,因此结果是离散的,我们采用分类算法。
如果我们要预测第四套房子的价格多少时可以售出,那么此时是否售出是“是”,y应该为房屋的价格。房屋的价格是连续的数字,有无穷多个可能,没有固定的数目,因此 不是离散的,我们采用回归算法。
2.监督学习深入介绍
2.1 监督学习三要素
模型(model):总结数据的内在规律,用数学函数描述的系统。
策略(strategy):选取最优模型的评价准则。
算法(algorithm):选取最优模型的具体方法。
2.2 监督学习实现步骤
1.得到一个有限的训练数据集。
2.确定包含所有学习模型的集合。
3.确定模型选择的准则,也就是学习策略。
4.实现求解最优模型的算法,也就是学习算法。
5.通过学习算法选择最优模型。
6.利用得到的最优模型,对新数据进行预测或分析。
2.3 模型评估策略
模型评估:
- 训练集和测试集
- 损失函数和经验风险
- 训练误差和测试误差
模型选择:
- 过拟合和欠拟合
- 正则化和交叉验证
2.3.1 训练集和测试集
我们将数据输入到模型中训练出了对应模型,但是模型的效果好不好呢?我们需要对模型的好坏进行评估。
我们将用来训练模型的数据称为训练集,将用来测试模型好坏的集合称为测试集。
训练集:输入到模型中对模型进行训练的集合。
测试集:模型训练完成后测试训练效果的数据集合。
2.3.2 损失函数
损失函数用来衡量模型预测误差的大小。
定义:选取模型f为决策函数,对于给定的输入参数X,f(X)为预测结果,Y为真实结果;
f(X)和Y之间可能会有偏差,我们就用一个损失函数(loss function)来度量预测偏差的程度,记作L(Y, f(X))
我们看其中的0 - 1损失函数,如果我们的误差非常小,我们可以认为这个模型很好了,但是该函数却一棒子打死,直接判1,因此效果不是很好。
我们再看对数损失函数,它是对条件概率的计算。我们知道概率永远小于或等于1,因此这个函数取负的原因就是使结果为正,也为了使它成为一个单调递减函数,这样,条件概率越大,损失函数越小,模型越好。
2.3.3 经验风险
2.3.4 训练误差和测试误差
2.3.5 过拟合和欠拟合
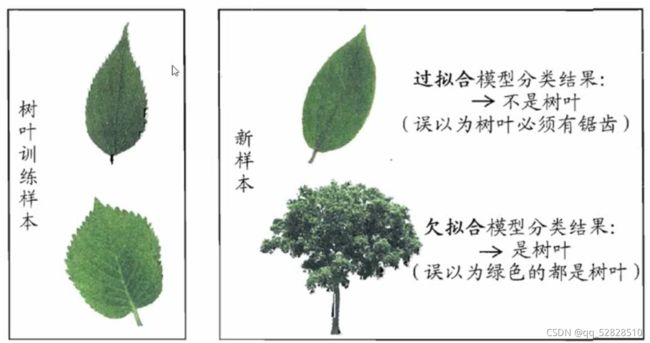
我们借用一张西瓜书里面的图
2.3.5.1 欠拟合
模型没有很好地捕捉到数据特征,特征集过小,导致模型不能很好地拟合数据,称之为欠拟合。
例如,想分辨一只猪,给出了一个嘴巴两只眼,两个鼻孔两只耳,那么人和猪都有,所以机器会认为,人和猪没有区别,这就闹出笑话了。
2.3.5.2 过拟合
把训练数据学习的太彻底了,以至于把噪声数据的特征也学习到了,特征集过大,这样就会导致在后期测试的时候不能很好地识别数据,即不能正确的分类,模型泛化能力太差,称之为过拟合。
例如,想分辨人和猪,给出了一个嘴巴两只眼,两个鼻孔两只耳,穿衣服的是人,不穿衣服的是猪,但是诶出的训练数据的人的图片中,人都是穿黑衣服的,那么这个黑衣服就是噪声数据,会干扰判断。如果我们给他一张穿粉色衣服的人的图片,那么机器就会认为他是猪。
黑衣服是局部样本的特征,不是全局特征,就造成了输入一个粉色衣服的人的数据,判断的是猪而不是人的笑话。
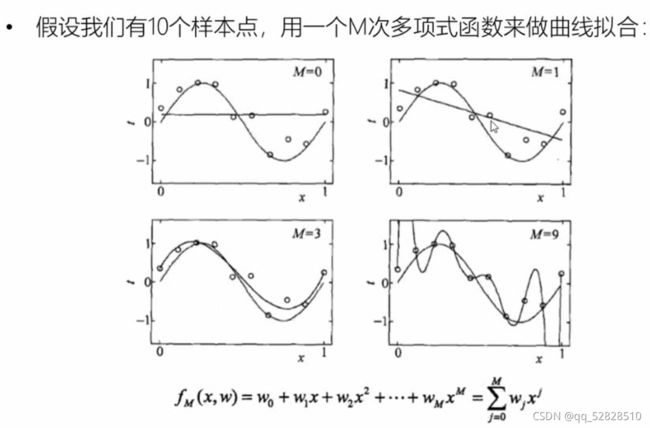
2.3.5.3 模型的选择
我们可以看到,当M = 0, 1时拟合的效果较差,可以称之为欠拟合;
当M = 3时,图像基本重合,拟合效果很好。
当M = 9时拟合效果又不好了,可以称之为过拟合。
2.3.6 正则化
结构风险最小化(Structural Risk Minimization, SRM)
- 是在ERM基础上,为了防止过拟合而提出来的策略
- 在经验风险上加上表示模型复杂度的正则化项(regularizer),或者叫惩罚项。
- 正则化项一般是模型复杂度的单调递增函数,即模型越复杂,正则化值越大。
L1范数简单的说就是绝对值求和。
L2范数简单的说就是平方和再开根号。
也就是说,分解出来的特征向量越多,维度越多,也就是说模型越复杂,这样的话惩罚也就越大。
2.3.6.1 奥卡姆剃刀原理
奥卡姆剃刀原理:如无必要,勿增实体。
正则化符合奥卡姆剃刀原理。它的思想是:在所有有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。
如果简单的模型已经够用,我们不应该一味地追求更小的训练误差,二八模型变得越来越复杂。
2.3.7 交叉验证
- 数据集划分
如果样本数据充足,一种简单方法是随机将数据集切成三部分:训练集*training set
、 验证集(validation set)和测试集(test set)
训练集用于训练模型,验证集用于模型选择,测试集用于学习方法评估。
- 数据不充足时,可以重复地利用数据——交叉验证
- 简单交叉验证
- 数据随机分为两部分,如70%作为训练集,剩下30%作为测试集
- 训练集在不同的条件下(比如参数个数)训练模型,得到不同的模型
- 在测试集上评价各个,培训的测试误差,选出最优模型
- S折交叉验证
- 将数据随机切分为S个互不相交、相同大小的子集;S-1个做训练集,剩下一个做测试集
- 重复进行训练,测试集的选取,有S中可能的选择
- 留一交叉验证
- 不管前面如何取,只留下一个数据进行验证。这种情况是数据量非常小的情况下才会去使用
3.分类和回归
监督学习问题主要可以划分为两类,即分类问题和回归问题
- 分类问题预测数据属于哪一类别 ——离散
- 回归问题根据数据预测一个数值 ——连续
这两个的概念在上文预测房价与房屋销售状况的例子中已经说明了区别。
3.1 分类问题
仍然是这张图片。
- 在监督学习中,当输出变量Y取有限个离散值时,预测问题就成了分类问题。
- 监督学习从数据中学习一个分类模型或分类决策函数,成为分类器(classifier);分类器对新的输入进行预测,成为分类。
- 分类问题包括学习和分类两个过程。学习过程中,根据已知的训练数据集利用学习方法学习一个分类器;分类过程中,利用已习得的分类器对新的输入实力进行分类。
- 分类问题可以用很多学习方法来解决,比如k邻近、决策树、感知机、逻辑斯谛回归、支撑向量机、不俗贝叶斯发、神经网络等。
3.1.1 精确率和召回率
评价分类器性能的指标一般是分类准确率(accuracy),它定义为分类器对测试集正确分类的样本数与总样本数之比。
对于二类分类问题,常用的评价指标是精确率与召回率。
通常以关注的类为正类,其它为负类,按照分类器在测试集上预测的正确与否,会有四种情况出现,它们的总数分别记作:
- TP:将正类预测为正类的数目
- FN:将正类预测为负类的数目
- FP:将负类预测为正类的数目
- TN:将负类预测为负类的数目
精确率:P = TP / (TP + FP)
- 精确率指的是“所有预测为正类的数据中,预测正确的比例”
召回率:TP / (TP + FN)
- 召回率指的是“所有实际为正类的数据中,被正确预测找出的比例”
3.2 回归问题
回归问题用于预测输入变量和输出变量之间的关系。
回归模型就是表示从输入变量到输出变量之间映射的函数。
回归问题的学习等价于函数你喝;选择一条函数曲线,使其很好地拟合已知数据,并且能很好地预测未知数据。
3.2.1 回归问题的分类
- 按照输入变量的个数:一元回归和多元回归。
- 按照模型类型:线性回归和非线性回归。
3.2.2 回归学习的损失函数——平方损失函数
为什么要用平方损失函数而不用绝对损失函数呢?是因为我们要求损失函数的最小值,而平方损失函数应该是一个抛物线的函数,方便求最小值。
即如果选取平方损失函数作为损失函数,回归问题可以用著名的最小二乘法来求解。
3.2.3 模型求解算法(学习算法)
- 梯度下降法
- 梯度下降是一种常见的一阶优化方法,是求解无约束优化问题最简单、最经典的方法之一。
- 梯度方向:函数变化增长最快的方向(变量沿此方向变化时函数增长最快)
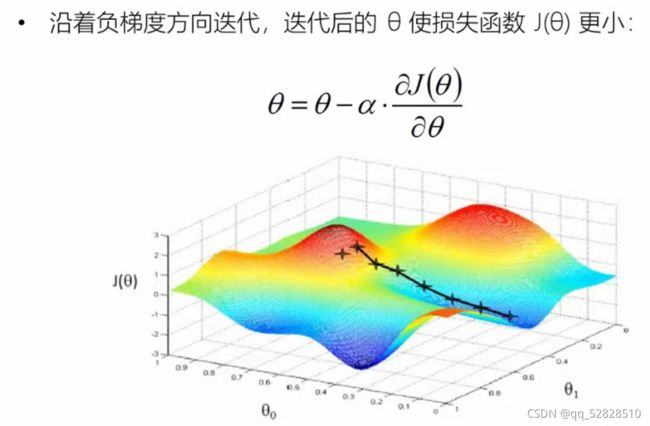
- 负梯度方向:函数减少最快的方法(变量沿此方向变化时函数减少最快)
- 损失函数是系数的函数,那么如果系数沿着损失函数的负梯度方向变化,此时损失函数减少最快,能够以最快速度下降到极小值。
α是调节系数,调节变化
- 比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山谷处。
- 从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。
- 如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
- 牛顿法和拟牛顿法